Оглавление:















Примеры
- Уравнение Крапейрона. При первом применении химического потенциала рассмотрим равновесие между 2 фазами однокомпонентной системы, состоящей из следующих элементов: Рассмотрим жидкость(1)и ее насыщенный пар (2). в случае равновесия в любой точке системы должно быть μ= const.In другими словами, химический потенциал μ должен быть одинаковым для пара и жидкости.Подобный этому ли < » = \ я <2).(6.21) Равенство (6.21) — это отношение P и T. Р = Р(Т),(6.22)
Поскольку | 1 (1) и / 1 (2) являются функциями P и T, то для каждой температуры формула(6.22) определяет соответствующее давление насыщенного пара P. функции и (1) и| a <2>соответствуют 2 поверхностям над плоскостью PT.Кривая давления пара [уравнение(6.22)] представляет собой проекцию пересекающихся линий обеих поверхностей на плоскость RT, которая должна заканчиваться в критической точке(см. рис.11).
Кроме того, обычно нет полной информации о функциях| i (l) и μ<2, но можно записать дифференциальную зависимость между Я и Γ, в том числе непосредственно измеряемую quantities.To получив его, рассмотрим 2 близких состояния равновесия (7 \ P) и (T—dT, P—dP).Для них, соответственно、 ^(1) / t(2) Поэтому также необходимо требовать: (6.24) Согласно уравнению (6.5), в соответствующей фазе находится N™=-5 (2)+ V (2) rfP. (6 ′ 25) (6.26) Когда я назначаю (6.24) на (6.25)、 ДП _ как _ как ДТ-ЗБ-Ш ’
Здесь строчные буквы обозначают определенное количество, которое присваивается 1 молекуле.s= S / N и так далее. Формула Клапейрона точна и может быть применена к любому фазовому переходу, не только переходу жидкость-пар, но и переходу твердое тело-жидкость, например 1). чтобы представить правую часть уравнения(6.26) относительно измеряемой величины, в этом уравнении (6.28)) (6.27) Где Q (см. Главу 4,§ 2) — количество тепла, поглощенного системой между переходами 1 — > 2.In в этом случае Q представляет собой теплоту испарения(при постоянном давлении) Qp- ^ пара^жадный-получить отношения таким образом (6.29)
Это уравнение крапейрона. Людмила Фирмаль
- В реальных приложениях часто используются следующие приближения: Рассмотрим Vnap^ RTjP \ Игнорируется по сравнению с Vnap. Рассмотрим теплоту испарения Q-и H-констант. ’) Правая часть уравнения as / AV Клапейрона может принимать вид 0 0.P. s. согласно Эренфесту (1931), этот случай соответствует переходу более высокого порядка. 2) Запишите предел отношения приращений lim (ЛР / ДГ) (n, = Q2 как полную производную.Если одновременно
Существует несколько фаз, то такая запись оправдана, так как P зависит только от T. ДП (ДП .Т (ДП \ дв ДТ ~~ [ДТ)г + [дв)ДТ# В насыщенной области (dPjdV) T = 0, поэтому последний член справа равен нулю. В случае фазы сжатие системы приводит лишь к переходу из одной фазы вещества в другую с меньшим удельным объемом, и давление остается постоянным до тех пор, пока одна из фаз не исчезнет полностью. Тогда, интегрируя уравнение(6.29), получим следующее соотношение: Р = Рое-м / РРТ(6> 30) Это удобная интерполяционная формула для ограниченной части кривой давления пара. Если не 2, а 3 фазы 1, 2 и 3 находятся в равновесии, то получаются следующие условия: =(6.31) То есть, есть 2 уравнения, соединяющие 2 независимых variables.So, решение (равновесие) может существовать только в некоторой изолированной точке 7 \ P-тройная точка.Хорошо известным примером является тройная точка воды при P = 4.58 мм рт. cm 7 = 0,01°C » твердая фаза, жидкость, пар сосуществуют.Даже однокомпонентная система может иметь несколько тройных точек (что на самом деле происходит в случае H20), потому что могут быть различные модификации твердого тела.Однако из условия равновесия(6.31) (2 уравнения, связывающие 2 переменные) видно, что максимальное число фаз чистого вещества, которое может существовать одновременно, равно
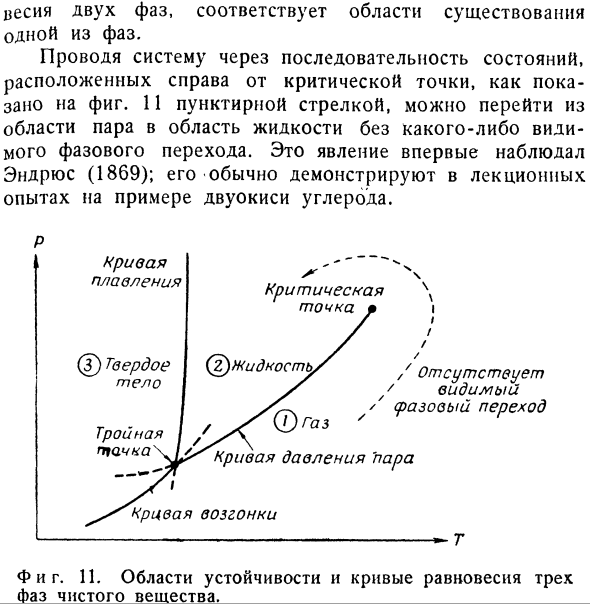
3. На рисунке 1 представлена принципиальная схема типичного случая.Область диаграммы P-T ниже критической температуры разделена на 3 части линией, пересекающей тройную точку. cO)= ^(2) — кривая давления пара, jjU) ^(z) — кривая сублимации, ji <2)= c (z) — кривая плавления. Пунктирная часть кривой давления пара| i (1)= | i(2) находится над поверхностью (P, T).Поэтому для того, чтобы свободная энергия была минимальной в этой области, вещество должно быть полностью фазой-3.Только твердая фаза стабильна в этой области.То же самое верно и для других 2 пунктирных линий.Таким образом, каждая область, заключенная в кривую, является
Веса 2 фаз соответствуют 1 области существования фазы. Как показано на фиг. Впервые это явление было замечено Эндрюсом (1869), и обычно оно демонстрируется в лекционном эксперименте на примере углекислого газа. П. С. х. \ что это? / / Недостающий. Видимый (1 максимальный переход Т. И фигура тоже. 11.Область Кривой равновесия со стабильностью 3 фаз чистого вещества. _ — Спросил я.Объясните, почему удельная теплоемкость насыщенного пара может быть отрицательной. (Среди задач, предложенных на экзамене Оксфордского университета 1962 года) Решение.Нам нужно найти dqjdt вдоль линии перехода Mpar = Skidk.It желательно рассмотреть отношения. dQ = dH-V dP- = с?в + Ш) Р ДП = с?ДТ-Т [W)П ДП> В этом случае последнее преобразование следует из термодинамического уравнения состояния(5.19).
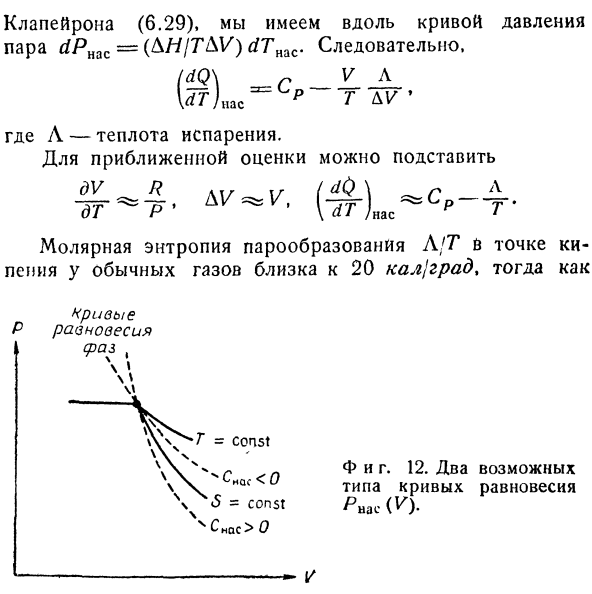
В соответствии с уравнением Клапейрон(6.29), вдоль кривой давления пара< / Янас=(ля / ГДС) RFT» AC.So … (йй \ = с-V-Денпасар.IrffLc п г Где L-теплота испарения. Для приблизительной оценки, вы можете использовать его вместо этого Л / ч температура кипения испарения молярная энтропия обычного газа близка к 20 кал / град, но、 Равновесия с-кривой(время、 В м. Мы И фигура тоже. 12. Кривая равновесия 2 возможных типов Явас (V). В среднем менее 10 калорий / hail.So мы видим, что при этой температуре (dQjdT) Me =Снс<0.So удельная теплоемкость насыщенного пара будет отрицательной. Как видно из сравнения термоизоляции и Изотерм на диаграмме P-V, знак Snas имеет определенное значение при сжижении газа(рис. 12). Кривая фазового равновесия всегда круче изотермы через точку конденсации.Если наклон этой кривой также превышает градиент изоэнтропии, то dT и dS имеют одинаковый знак в каждой точке фазового равновесия curve.So, (dQfdT) nac> 0:если кривая фазового равновесия проходит между изоэнтропией и изотермой, то dT и dS имеют разные знаки, а производная dQjdT отрицательна.И фигура тоже.
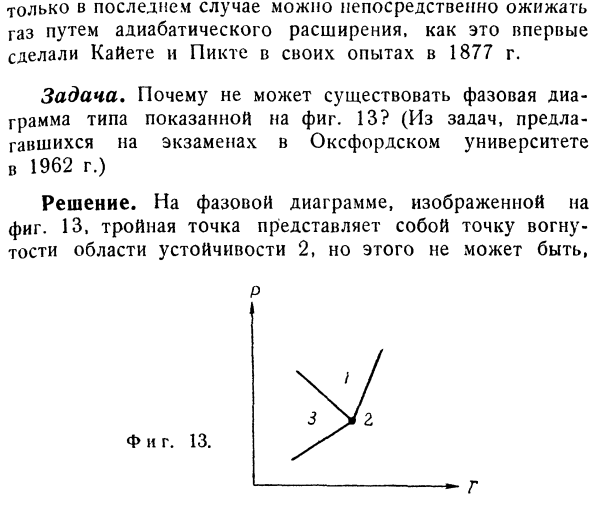
12. Только в последнем случае, как это впервые сделали Кайете и пикет в своих экспериментах в 1877 году, газ может быть непосредственно сжижен путем адиабатического расширения. — Спросил я.Почему государство Рисунок 1, как показано на рисунке 13? (Среди задач, предложенных на экзамене Оксфордского университета 1962 года) The solution.In на диаграмме состояния, показанной на рисунке 13, тройная точка представляет собой вогнутую точку стабильной области 2, это невозможно. П. С. Г. Это объясняется тем, что продолжение кривой фазового равновесия (1, 3) должно находиться над поверхностью ji (2) (Р, Т).Если нет, вы можете получить энергию, разделив фазу 2 на фазы 1 и 3, которые присутствуют одновременно.Это невозможно.Это связано с тем, что область 2 представляет собой область существования стабильной однородной Фазы 2, и поэтому соответствует минимальному значению свободной энергии.
Есть также еще 1 свойство на рисунке, которое термодинамически возможно, но все же довольно необычно.Это означает, что 1 из кривых фазового равновесия имеет отрицательный наклон, dPjdT.Однако это свойство можно наблюдать.Хорошо известный пример-вода. / = Диаграмма состояния вокруг тройной точки пода вблизи 0°C показана на Рис. 2. 141).Вот такая ситуация. 1) Другим примером является близость точки L выше. Фазовая диаграмма HE4. Тот факт, что кривая таяния льда характеризуется отрицательным градиентом, вероятно, важен для коньков. Кривые плавления. Кривая сублимации 0t0098°с F и d 14. t = диаграмма состояния 0°вблизи C H20 Лед я 4.58 мм рт. см.
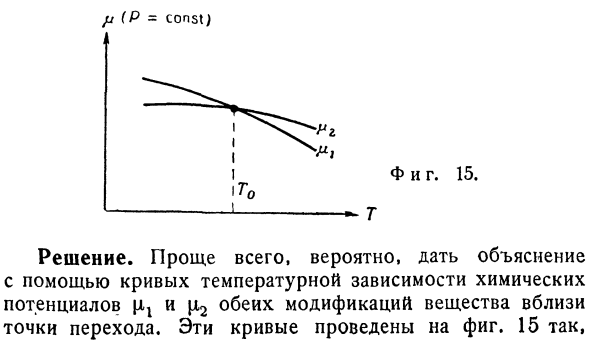
- Кривая давления пара — Спросил я.Объясните, почему скрытая теплота, соответствующая переходу вещества от низкой к высокой температуре (определяемая как теплота, поступающая в систему при изотермическом изобарном преобразовании), всегда положительна. (Среди задач, предложенных на экзамене Оксфордского университета 1962 года) //(Р = const) Решение.Самый простой способ-объяснить с помощью кривой химического потенциала\ ix и / i2 температурную зависимость обеих модификаций вещества, возможно, вблизи точки перехода.Эти кривые изображены на фиг. 15.
Его Фаза 1 соответствует высокотемпературной форме (стабильной в диапазоне температур, превышающем T0).Скрытая теплота, в зависимости от рассматриваемых условий, равна hx — h2 = T0 (sl — s2).Тем не менее, s = — д \ ifdT, а в точке перехода, производной д \ xJdT должен быть меньше, чем D [12 / ДТ.Поэтому, при необходимости, разницу-Н2 является положительным. 2.Идеальный газохимический потенциал.1.
Полное дифференциальное интегрирование =»N + V dP)(6 32) Идеальный газ. U и V = я С. С. Возвращает выражение С = — Р \ НП + КП \ НТ + С0,г = В0-fCpT4-РТ ИНП-т(Срinт + С0), (bii4) Первое, с чем мы уже столкнулись при рассмотрении изэнтропий(см. Главу 2,§ 6, стр. 1).Интегральная константа С0 = С(П-1, Т = 1) (6.35) H = H0 + CPT и(6.33) Не определен.Как это можно определить по измерению давления пара, описано ниже (см. Главу 8). Для чистого вещества химический потенциал равен потенциалу Гиббса, присвоенному 1 молекуле, и равен μ= G / N.It принято записывать следующее я ^ о ^ ЛНП — с-лнт-Т,(6.36)
Идеальный газ — одна из немногих систем, настолько простых, что она может немедленно описать термодинамические функции. Людмила Фирмаль
Где, согласно формуле (6.34)、 (6.37) , _(Г-с />) Р’. значение i иногда называют химической константой.Константа e0 в Формуле (6.36) зависит от выбранной точки отсчета энергии.Эта константа всегда имеет вид Например, e0 (^2)-2e0 (H) — энергия диссоциации молекул H2 на свободные атомы N2.Это избавляет от необходимости рассматривать начальное состояние (1) для его исправления. Статистическая механика позволяет, по крайней мере частично, вывести из данных молекул все величины, которые фигурируют в феноменологической термодинамике.Например, для моноатомного идеального газа、 5 / 2lt y / 2 и 2 -<=, н (т) к ’<638> Где t-масса молекулы, а h-постоянная Планка. В соотношениях (6.36) и (6.38) размерная величина является аргументом логарифмической функции.
Этот факт кажется не совсем логичным, но его смысл заключается, конечно, в том, что вся правая часть уравнения, включая константу интегрирования (6.36), дает логарифм безразмерного произведения.Обратите внимание, однако, что все величины должны быть выражены в одной и той же системе единиц.Это иллюстрируется примером, рассмотренным в разделе. 8,§ 3.
Смотрите также:
| Примеры | Смеси |
| Системы с переменной массой. Химический потенциал | Соотношение Гиббса — Дюгема |

