Свойства интеграла

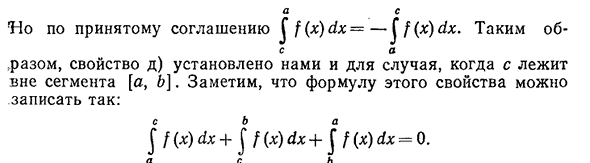
Свойства интеграла

• Неотъемлемое свойство. Рассмотрим основные характеристики интеграла Римана. а) пусть функции f (x) и g (x) интегрируемы с отрезками[a, 6]. Тогда функция f (x)±g (x) также интегрируема в этом

сегменте, и b b (f (x)±g (x)) dx={f (x) dx± ля. f g (x) dx. Для любого выбора любого раздела и средней точки gсегмента[a,B] справедливо следующее равенство: [f (&g)±g (Efe)]^x k=£f(&g)Axk+£g(gA) DHA. fc=l k = l A = 1 Итак, если диаметр перегородки стремится к нулю

,если есть предел правой части, то есть предел левой части. Из линейного Людмила Фирмаль

свойства этого ограничения, которое устанавливается таким же образом, как и предел последовательности, доказываются следующие свойства:348CH. 9. Очистить Интеграл Римана b) если функция f(x) интегрируема в сегментах[a, B], то функция cf(x) (C=const) также

интегрируема в этом сегменте.、 b§cf (x) dx=c$f (x) dx. один В общем случае для любого выбора любого разбиения и середины отрезка[a, 6] будет выполнено соотношение V cf ()£\x k=C Y f(&)\x k , U2 (x)=0 и разбиение{xk}таких отрезков[a,B]S-s}{для суммы S и s выше и ниже x все неотрицательные члены (Mk—mk)\xk выражения S—S также являются членами выражения S’-s’-s’, поэтому очевидно, что

• отношение S-S^S’-s’ — S ‘ удовлетворяется, поэтому s0. Пусть {Xk}и{x/’} — разбиение отрезка-fa, C]и[C, d] каждый из этих отрезков S равен s< & l2. Сделайте {X^Раздел для сегментов[a,&] {XG}и{Xk»}. Ясно, что разница между верхней и нижней суммой разбиения{x*}не превышает E. пусть {Xk} — любое разбиение, включая отрезки[a, C. Затем £ф (г\х

К=С Альф (&) Axfe+2″, ф&) т=я, где s’является, предпринимаемые суб-сегмента, принадлежащих[а,СЖР Ы» — [С, D]. Это относится к любому разделу, поэтому, когда диаметр раздела достигает нуля, достигается предел、 б е д Буквы ‘J Ф (Х)DX=J и Ф (Х)DX+J и

Ф (Х)DX. И еще и еще Если c не принадлежит[А,B], тогда segmert[а,&] Людмила Фирмаль

принадлежит[П,&] или[А, С]. Например,_с хорошо с * Функция точки a определена и принимает конечное значение..- 350Ч. 9. Очистить Интеграл Римана Но договор акцепта J F по C (x)dx= — §f (x) dx. Таким образом, если c находится вне отрезка[a, 6], то свойство d)устанавливается нами. Выражение для этого свойства можно записать в виде: Дж. Ф(Х) D Х+^ф(х)D Х+§ф (х)DX-0. один

Смотрите также:

Методическое пособие по математическому анализу

Условия монотонности функции на интервале	Свойства интеграла
Существование и вычисление криволинейного интеграла второго типа.	Краткие сведения о корнях алгебраических многочленов