Оглавление:
























Перенос тепла в разреженных газах
- При обычном рассмотрении теплопередачи газов структура газа считается непрерывной, поэтому нет необходимости включать представления о молекулярной структуре газа. Поток и явление Теплопередача при условии непрерывности такой среды может быть адекватно выражена через стандарты Рейнольдса, Маха, нуссельта и прандля. Однако, если абсолютное давление низкое, то газ Возникает явление, которое может быть объяснено только при частичной утрате характерных свойств непрерывности и учете мыслей о молекулярной структуре Газ.
Изучение аэродинамики теплового потока и теплообмена в разреженных газах было начато сравнительно недавно, и многие другие фундаментальные проблемы требуют решения путем анализа и экспериментов. Основой для рассмотрения этих явлений является кинетическая теория газов, впервые разработанная количественно Даниэлем Бернулли в 1738 году. Эта теория рассматривает газ как пространство、 Он заполнен молекулами, движущимися по прямой траектории и отклоняющимися только при столкновении с другими молекулами. Средняя кинетическая энергия молекулярной популяции Определите температуру gas. It считается, что столкновение происходит по закону упругого удара.
Во внутреннюю энергию не включают те составные части полной энергии, которые не меняются при изменении макроскопического состояния системы. Людмила Фирмаль
Статистическая средняя длина линейных путей между молекулярными столкновениями Это называется средним свободным путем молекулы X, и скорость каждой молекулы меняет направление в столкновениях. (Следовательно, молекулы различных скоростей всегда доступны. Поскольку скорость большинства молекул близка к средней скорости v, существует несколько молекул с очень большой или очень низкой скоростью. Распределение скоростей молекул в Газе Состояние равновесия составляет 1,859 Дж. С. Оно вычисляется по Максвеллу и называется распределением скоростей Максвелла.1. один из первых успехов в кинетической теории газов Предсказание удивляет тем, что динамическая вязкость и теплопроводность идеального газа не зависят от давления.
Это означает, например, что определенное количество тепла Он проходит через неподвижный слой газа при постоянной температуре, независимо от давления газа. С вязкостью используя упрощенную концепцию Теплопроводность. Кинетика объясняет напряжение трения текучих газов тем, что молекулы перемещаются взад и вперед между слоями газа, протекающего с разной скоростью. velocities. So … Так, молекулы из газового слоя с малой скоростью входят в газовый слой, двигаясь с большой скоростью, и после нескольких столкновений их скорость увеличивается и скорость увеличивается. Молекулы столкновения уменьшены. Поэтому происходит обмен импульсами между слоями газа.
Если молекулы совершают одно и то же движение, то обмен энергией происходит, когда они находятся в Газе Расположение разности температур. Рассмотрим ламинарный газ, параллельный стенке, со скоростью, перпендикулярной стенке, и градиентом температуры (рис.10-9).Молекулы движутся вперед. Затем вернитесь назад через любую плоскость АА, параллельную стене. В течение временного интервала dr через него проходят молекулы с компонентной скоростью r≥1 перпендикулярно плоскости aa. Самолет на расстоянии от самолета. Число молекул в единице объема равно N, а средняя составляющая скорости в направлении плоскости АА всех молекул Часть средней молекулярной скорости.
Таким образом, все молекулы в объеме i’VDX проходят через единичную площадь плоскости. Число таких молекул равно i’nvdx, а число молекул равно С другой стороны, прохождение через единицу площади плоскости aa за единицу времени равно i’NV. Числитель характеризуется расходом от предыдущего столкновения до следующего. Итак, в среднем мы перемещаем скорость потомства из плоскости/ −1 в плоскость 2-2, рис. 10-9.Молекулярно-энергетический обмен. Средняя длина X разделяется расстоянием порядка Средний свободный путь молекулы. Это расстояние / X показано. Здесь j не может сильно отличаться от 1.
Молекулярный поток такого же размера проходит через поверхность АА Направьте поток в противоположном направлении и передайте скорость потока d ’ со стороны 2-2 в сторону 1-1.Обмен импульсами, связанный с этим процессом, выглядит следующим образом: i’NVM, (a-and’), m is 1. масса молекул. Если градиент скорости на плоскости aa в направлении, перпендикулярном плоскости, равен dujdy ^(и-и’), то его можно выразить как jX (du / dy), а значит, заменить Импульс или напряжение трения на единицу площади: x = i’nnmvx = inmvl * J DY DY продукт i’j может быть представлен Z. вязкость p Уравнение x = >.определяется (дю,[ды).Если мы сравним с формулой m выше, мы найдем p-inmvl. Продукт pt-это масса p на единицу объема. Тщательный расчет S. Chepman и D.
Для глобулярных молекул, что объясняет распределение молекулярных скоростей, создаваемых Easkog, так как значение численного коэффициента i равно 0,499、 Динамическая вязкость| л = 0,499 ruA. (10-23) показывает ли кинетическая теория p? Формула R, выражающая среднюю молекулярную скорость независимо от давления — Газовая постоянная исследуемого газа; T-абсолютная температура. Поэтому, и, как видно, она не зависит от давления. Если градиент температуры DT \ dyy обмен осуществляется в Газе Тепло происходит так же, как и обмен импульсами между молекулами.
Если st — теплоемкость молекулы, то тепловой поток на единицу площади плоскости АА равен следующему. — г. ДТ г = / гной з-Т -. когда объем cᵥ на единицу массы m dy является постоянной удельной теплоемкостью, устанавливается соотношение ncₘ=pcᵥ.Теплопроводность определяется Уравнение х = КЖ(dtldy).Если подставить эти величины в Формулу q, то получим: X = Mpc)=pcᵥ(10-24) следовательно, эта простая теория имеет вид、 Механические и тепловые свойства. Предполагалось, что они совершенно не связаны между собой. Формула (10-24) дает приемлемое значение, но не соответствует эксперименту Однако можно установить числовой коэффициент, вычислительная матрица которого дает хорошее соответствие.
Дальнейшая обработка расчет теплопроводности Поскольку теплопроводность является более сложной характеристикой, она сложнее, чем обработка вязких расчетов. Коробейник. 158] показал, как производилось вычисление, и получил следующее выражение Соглашение 1 этот результат не применяется к газам очень высокого давления, где вязкость зависит от давления. Шума в экспериментальных Это одноатомные данные, но не более сложная молекула. Формула имеет следующий вид:(Yu-25) Aiken [L. 159]была получена следующая формула для теплопроводности сложных молекул: ^7₄ (9y-5)^, (10-26) хорошо согласуется с экспериментальными данными простых и сложных молекул. y-отношение удельной теплоемкости при постоянном давлении. Постоянный объем.
Из Формулы (10-26)’.Вы можете написать формулу критерия Прандтля, основанную на кинетической теории: отношение Pr±(10-27) (10-27) очень хорошо Он согласуется с тестовыми значениями Прандтля, рассчитанными по результатам измерений. Критерий Рейнольдса также может быть выведен на основе кинетической теории. Р — » 0,499-• (10-28) следовательно, критерий Рейнольдса является произведением отношения между скоростью и длиной. Отношение скоростей-это макроскопическая скорость потока и Средняя молекулярная скорость y; отношение длины — отношение среднего свободного пробега размера тела I к среднему свободному пробегу молекулы I. аналогично.
Возвращает значение критерия Маха. Форме выражения для скорости звука выглядит следующим образом:=, следовательно, из представления средней молекулярной скорости, получим»’».«»/Г следовательно, число Маха (10-29) то есть число Маха пропорционально отношению макроскопической «скорости V» и средней молекулярной скорости V. При нормальном давлении расстояние между молекулами, даже если это газ, равно、 Если расстояние между молекулами очень велико по сравнению с твердым или жидким телом, то оно будет намного меньше размеров тела, обычно обрабатываемых при расчете Понятие теплопередачи, а следовательно и непрерывного газа, может быть применено здесь в моде (газ считается континуумом). при низком давлении соответствующая низкая плоская длина Средняя длина свободного пробега молекулы х сопоставима с размерами тела, и влияние молекулярной структуры начинает влиять на механизм течения и теплообмена.
Родственник Значимость эффекта разрежения газов может быть продемонстрирована путем сравнения среднего свободного пробега молекул газа с характерным размером тела. Итак, если I-размер тела, а это характерный размер поля потока, то влияние разрежения на поток и теплообмен будет заметно, как только соотношение перестанет получаться Игнорируй больше. Это соотношение безразмерно и определяется как критерий Кнудсена. Кнудсен нормирует, а потому непосредственно заинтересован в изучении течения Разбавленный газ и теплопередача, ’Mach’ и могут быть выражены в терминах Рейнольдса: K T = T = | / f («0-30) y = 1.4 Tzin [L. 160]предложение В зависимости от соответствующего интервала критерия Кнудсена рассмотрим механизм явления газов.
Для потоков с низкой вязкостью (то есть, если значение критерия велико) Рейнольдса) наиболее важным характеристическим размером является толщина пограничного слоя d. отношение толщины пограничного слоя к ламинарному течению составляет Если характерный размер тела равен 1, то соответствующее значение критерия Кнудсена будет: Kn = b ^ — ⁽1°-31⁾нормальный газ Поэтому динамика происходит при Re> 1, а отношение M / j / Re пренебрежимо мало. Для медленных потоков, таких как поток Стокса, характерным измерением потока является размер Итак, если критерий Кнудсена основан на величине Z, то: следовательно, если отношение M / Re пренебрежимо мало, поток можно считать непрерывным потоком. Этого недостаточно.
Для потоков, где значения критерия Рейнольдса в среднем большие, а значения критерия Маха большие, критерий кнусена уже не может получить такое значение — Замечать и указывать на наличие эффекта разбавления в потоке.1 continuous. In течение, обычные граничные условия на границе раздела газа и твердой поверхности следующие: В том, что газ на поверхности принимает скорость и температуру поверхности.1. одним из наиболее интересных эффектов разбавления газа в потоке является то, что газ примыкает к твердому телу Не принимает поверхность, скорость поверхности и температуру. Касательная скорость газа на поверхности равна finite. It «скользит» по поверхности.
Температура газа на Поверхность, в конечном счете, отличается от температуры поверхности. Происходит «скачок» между поверхностью и температурой соседнего газа. Эти эффекты связаны со средним значением Средний свободный путь молекулы, а также параметр называют коэффициентом аккомодации и коэффициентом отражения, который описывает статистическое взаимодействие поверхности с 1 Продолжения указывают на то, что поток считается континуумом. (Примечание, редактировать) молекулы. Вышеупомянутый стиль потока называется скользящим стилем потока, хотя он происходит в небольшом масштабе.
Это не ничтожное значение Кнудсена criterion. At очень низкие плотности, средний свободный путь X намного больше, чем любая характеристика Тело size. In в этом случае молекулы, покидающие поверхность тела, не сталкиваются с молекулами свободного течения до тех пор, пока они не окажутся далеко от поверхности. Как? В первом приближении в этом случае можно предположить, что молекулярное распределение в области, удаленной от поверхности, не искажается, то есть оно является Максвелловским, так что течение вблизи тела не искажается. Его можно рассматривать с точки зрения взаимодействия между свободными молекулами и поверхностями. Такая схема течения называется свободномолекулярным потоком или потоком Кнудсена.
Переход от газодинамического режима к режиму свободного молекулярного течения является постепенным и не имеет экспериментального разрыва, но полезен для аналитических целей Режим течения определен, но это несколько произвольно. Тзин ввел некоторые диапазоны таких значений. Газодинамика-7 = — 0,01; V Re свободный молекулярный поток Yu-область между ними занята скользящим потоком и переходным режимом течения. Переходный режим подачи, с сползая потоком Свободное течение молекул характеризуется тем, что средний свободный путь молекулы имеет примерно те же значения, что и характерный размер тела. Столкновение между Молекулы и поверхности, и между молекулами происходят часто, одинаково важны.
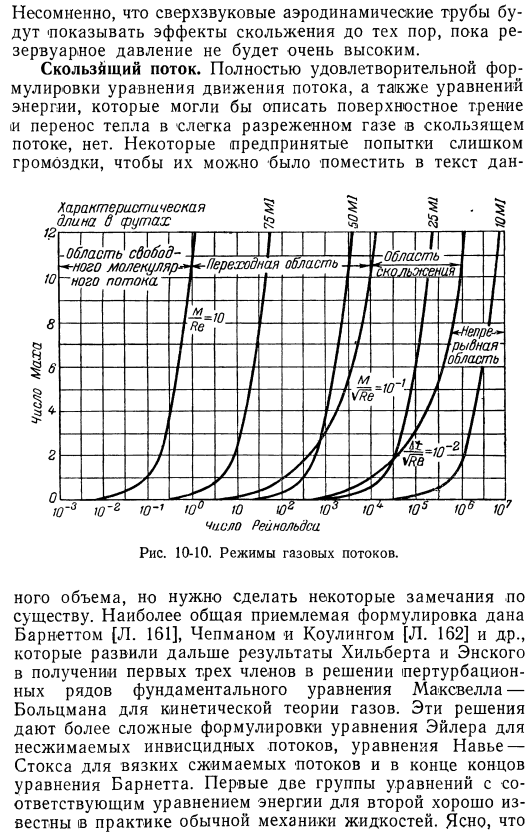
Анализ этой области затруднен. Имеющиеся данные в большинстве случаев недостаточны- Я испытал это на себе. Эти области потока показаны графически на диаграмме. В качестве параметра высоты на 10-10, высота (в милях) над уровнем моря соответствующей высоты 0,305 метров. Из рисунка Даже с 10 до 10 умеренно высокими стандартами Маха ясно, что ракета, летящая на высоте 32 км, будет испытывать эффект ползучести. M> 4 сжимаемый пограничный слой Обеспечивает эффект скольжения на эталонное значение Рейнольдса менее 10yn. Без сомнения, в сверхзвуковой аэродинамической трубе、 Пока давление в резервуаре не станет очень высоким.
Скользящие потоки. Полностью удовлетворительная формулировка уравнения движения потока и уравнения энергии Некоторые » попытки объяснить поверхностное трение и теплообмен слегка разбавленного газа в скользящем потоке не укладываются в громоздкую схему Положите в текст этого тома, но вам нужно сделать несколько существенных замечаний. Наиболее общепринятой формулы Барнетта [л. 161], Чепмен и каулинг[л. 162]другие Развивая далее результаты Гильберта и энски, мы получили первые 3 члена решения основного ряда турбулентности Максвелла-уравнения Больцмана Кинетическая теория газа.
Эти решения обеспечивают более сложную формулировку уравнений Эйлера для несжимаемого невязкого течения и уравнений Навье-Стокса для вязкого сжимаемого течения. В конце концов, уравнение Бернетта. Уравнение энергии, которое соответствует первым 2 группам уравнений и 2-й, хорошо известно в обычной практике hydrodynamics. It понятно Уравнение Барнетта, как и уравнение Навье-Стокса, имеет более высокую производную, чем уравнение Навье-Стокса, и、 Уравнения Эйлера идеального течения. Например, относительная важность этих членов более высокого порядка в формулировке Барнета по сравнению с членами в уравнении Навье-Стокса Как упоминалось ранее при определении условий течения, разрежение определяется размером параметров.
Например, в уравнении Бернетта термин Далее: Р.2да 1 /да. di \ 7 ’dh ’ 2 \ d «/ dx) ’ P получается путем деления его на член, представляющий напряжение в уравнении Навье-Стокса. Да. И 2м2 ’ДХ п «ручьи» — R e ’следовательно, термин имеет порядок величины в соответствии с размерами стандартов Маха и Рейнольдса и, исходя из ранее рассмотренных соображений, не может быть проигнорирован. Малый в зоне сползая подачи. Другие члены уравнения Бернетта имеют тот же размер. Вышеприведенные понятия могут быть применены строго к одноатомным газам. Есть только 3 степени свободы для перевода. Для двухатомных и многоатомных газов распределение внутренней энергии по всем степеням свободы не происходит до тех пор, пока она не пройдет.
Время релаксации после внезапного изменения газообразного состояния. Внутренняя энергия сначала накапливается в поступательных степенях свободы, и только после достаточной Накапливается количество столкновений, степеней свободы вращения и вибрации. Необходимое количество столкновений варьируется от нескольких раз в случае с воздухом до более чем тысячи СО₂.Например, толщина ударной волны почти полностью определяется высшими уравнениями, но это очень сложно. Несмотря на большие трудности、 Есть много работ, которые возникают из попыток сформулировать проблему скользящего течения, и часто, именно из-за них, раскрывают эффект скользящего течения.
Газ. Аналогичные положения сохраняются и для уравнений Навье-Стокса, но общего решения нет, а есть лишь несколько частных решений. Но их очень много (Примерное решение, позволяющее использовать соответствующие понятия на практике. Исследование скользящего потока часто выполняется очень грубо. В связи с тем, что анализ был основан на уравнениях Навье-Стокса, он обычно используется для несжимаемых течений. Решение приблизительное, а явление есть Скольжение учитывалось путем введения дополнительных членов в граничные условия тангенциальной скорости и температуры.
То есть учитывались промахи и скачки температуры. На границе поверхности с газом. Несмотря на неточность допущений, использованных для учета эффекта скольжения, результаты были проверены экспериментально и оказались весьма полезными Точность. Еще одним интересным и в то же время удивительным результатом является то, что в большинстве случаев он был получен при анализе скользящего потока, но результат близок Если критерий Кнудсена признан очень большим, то он соответствует результату свободного молекулярного течения.
- Гипотетический скользящий поток является Явления, связанные с малым числом Кнудсена, точное значение этого явления неизвестно, но этот факт был успешно использован в полуэмпирическом анализе для согласования .Экспериментальные данные всего течения от газодинамики до свободномолекулярного течения. Приближенный анализ скользящего потока. Потому что нет тока Если существует прямое решение уравнения течения и энергии в области скользящего течения, то задача рассматривалась с использованием обычных уравнений течения и энергии. Эффект разрежения в граничных условиях. Мы рассмотрели 2 основных эффекта явления скользящего потока. Во-первых, это было показано теоретически Максвеллом и экспериментально Кунта и Варбурга вблизи границы, скорость потока не равна нулю, и поток скользит вдоль стенки с конечной скоростью.
Во-вторых, скачок температуры Доказательство Пуассона возникает, когда тепло передается от поверхности к разбавленному газу, и в эксперименте смолковского [L. 163]этот эффект Статическая система. Эти эффекты могут быть математически выражены в следующем уравнении:«,= o — ^ = VxC^) ⁽ ⁽1⁰ ’ 32 32 (10-33) где fₛ-коэффициент зеркального отражения、 Или доля тангенциального импульса молекул, сталкивающихся с wall. It передается на стену. а-температурный коэффициент, или указанное значение.
Насколько молекулы газа при отражении (или излучении стенкой) воспринимают энергию молекул на поверхности wall. So, a может быть выражено как: =(10-34), это записывается для идеального одноатомного газа, но вы можете точно приблизить его для других целей gases. As в (10-35) формула (10-34) E Энергия молекулы, которая отражается (или излучается) от поверхности. Er-энергия молекул в случае поверхностного свободного течения, а Ew-энергия, соответствующая энергии свойства. Surface. In уравнение (10-35), t поверхность-это температура молекулярного потока, который отражается (или излучается) от поверхности. ті-температура падающего молекулярного потока. tw-температура поверхности или стены. Коэффициент отражения fₛ и коэффициент регулировки a считались более вероятными для экспериментального определения Чем в качестве переменного параметра.
Так, при обычных температурах в состав внутренней энергии не включают энергию атомных ядер, ибо она в этих условиях не меняется. Людмила Фирмаль
Внутри таблицы. 10-1, Milliken [L. 164]и Blanken-коэффициент зеркала Газовая поверхность fs обработанная воздухом бронза (латунь, медь) 1.00 CO2 тот же 1.00 Air old shellac 1.00 1.00 1.00 СО2 тот же воздух НД Ш нефть 0.90 СО2 Н Н2 Н 0.92 0.93 0.89 0.87 воздуха стекло без масла воздуха Свежий шеллак 0.79 W Ag2O не 0.98 ag2o 1.00 H2 Ag2O O2 Ag2O 0.99 mat[L. 165]. как видно из таблицы, в первом приближении f1 может быть «равна 1». 10-2 дает некоторое значение Кнудсен (L. 166), Оливер [L. 167], Вейдман и Траумплер [L. 168], Робертс [L. коэффициент теплового регулирования на основе 168]a. In таблица 10-2, тепловые коэффициенты Корпус газовой поверхности в N2 светло-платиновый темно-0.74 0.32 Н2 О2 свет 0.81 02 .
Темный 0.93 N2 платина 0.50 N2 вольфрам 0.35 бронза airlucker 88 — 0.89 полированная бронза 0.91 — 0.94 9 отделка 0.89-0.93 9 бронза вытравливания 0.93 ~ 0.95 9 отполированное литое железо 0.87 ~ 0.93 9 отделка 0.87 ~ 88 9 Чугун соленья 0.89-0.96 9-польский алюминий 0.87 — 0.95 9 отделка 0.95-0.97 9 маринованные алюминиевый 0.89-0.97 не вольфрам На практике эти значения рассматриваемой системы могут быть определены, так как коэффициент регулирования 0,025〜0,057 обеспечивает достаточно большое количество значений. Плоская пластина. На примере задачи Рэлея о бета-пластине, запускаемой импульсно, можно рассмотреть ламинарное скольжение потока по плоской пластине с нулевым углом attack. In это дело、 Навье-упрощенная формула для инерции и вязкости уравнений Стокса.
Рассчитайте сначала сопротивление пластины, а затем теплопередачу от той же пластины. * Поток является Он учитывается в двух измерениях, но в случае ударно запущенных пластин, элементы конвективной инерции, такие как (di / dx), и значения вязкости v (d2i! dh2) можно игнорировать. Остальные члены di_ _ d ^и dx — ^ du * * слева могут быть преобразованы в di _ _ di dx. если di du dx dx ’ dx ’ du ’ dx (10-36)и изометрический u передаются на пластину только в направлении X, то эта формула сводится к форме ДиДжей, Ди ДХ ~~ ДХ у ду / ДГ уравнение (10-36)принимает вид: Ди _ _ _ _ ДХ Vdu2d (10-37) соответствующее граничное условие Ниже: u = U \ x = 0; y> 0; » PL: g /PL: x>⁰; x > °—2-е граничное условие записывается в условие скольжения скорости коэффициента отражения зеркала, равное .
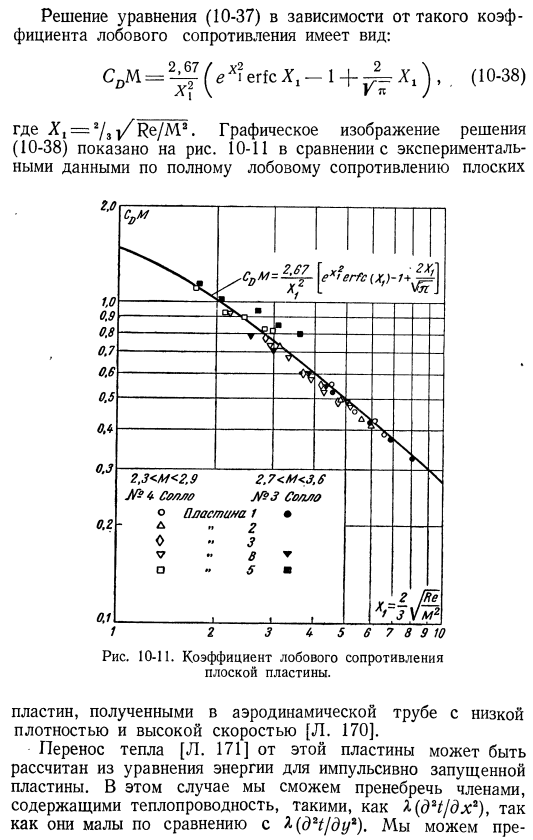
1.Коэффициент Сопротивление определяется как общее сопротивление 2 сторон пластины на единицу ширины rb’2/ / 2, согласно которому решение уравнения (10-37 Формат коэффициента сопротивления выглядит следующим образом: CDM= ^(eA? erfcXI-14-ⱼ^X₁), (10-38) где X,=2/зi / Re /M2.Графическое представление решения (10-38) показано на рисунке. 10-11 дюймов Сравнение с экспериментальными данными по полному лобовому сопротивлению плоскостей 10-11.Коэффициент лобового сопротивления плит. Полученные пластины в Низкая плотность, высокоскоростная аэродинамическая труба[L. [170]. * Теплопередача[L. A. 171]от этой пластины, она может быть рассчитана из уравнения энергии на импульсе.
Игнорируется plates. In этот случай, I. термины, содержащие теплопроводность, такие как (d2//dh2), можно игнорировать, поскольку они малы по сравнению с TsdN /du1.Вы можете сделать это заранее Если мы проигнорируем термин, описывающий конвекцию как » y\», то уравнение энергии примет вид: du ’(10-39) Соответствующие граничные условия приведены с учетом условий температурного скачка стенок и состояния свободного течения. t = tf \ x = 0; / / > 0.So, если a = 0,8, то y = 1,4; решение Форма уравнения выглядит следующим образом:(10-39)(10-40)е2erfcX₂-1 здесь Xₐ=)/ RePr/6,9М2 и критерии St-Stanton: NuaRe Pr U? cₚ с кем я могу работать Сравните решения(10-40).
Однако решение(10-40) должно давать такие же хорошие результаты, как и Формула (10-38).Мяч. Отмечается теплопередача от пара Сферическая форма хорошо работает в экспериментах [L. [172].Однако в большинстве случаев, когда диаметр шара не очень мал, значение критерия Маха усложняется задачей. Он должен быть большим, чтобы стандарт Кнудсена был достаточно большим для создания скользящего потока. Это обычно означает, что число Маха таково, что поток становится supersonic. So …
В этом случае перед шаром возникает ударная волна (рис.10-12), и условия, стоящие за этой ударной волной, следует учитывать при расчете теплопередачи.1. как одна из моделей、 вы можете рассмотреть шар в сверхзвуковом разреженном потоке газа с предыдущим нормальным скачком плотности y, а за ним можно вычислить свойства газа Определите тепловое искажение. В качестве 2-й модели можно рассматривать разреженные дозвуковые потоки, которые могут быть получены при очень низких плотностях при отсутствии компрессионных воздействий.
Его анализ (поэтому он не особенно сложен (л. 173).Кабанов привел формулу для коррекции разрежения к раствору для теплопередачи от шара в случае непрерывного действия. Это подтверждается экспериментальными данными с точностью до 10%.Теперь рассмотрим это приближение. Рис. 10-12.Ударная волна перед шаром (метод послесвечения) Азот.)Рассматривая температурный скачок в области скользящего потока как эффективное тепловое контактное сопротивление в пространстве между газом и поверхностью、 Эквивалентное или более высокое тепловое сопротивление за счет вязкости (пограничного слоя), коэффициент теплопередачи при низкой плотности можно определить в первом приближении Коррекция коэффициента теплопередачи сплошной среды при одном и том же значении критерия Рейнольдса.
Рассмотрим поверхность непрерывного потока, через который тепло передается между Поверхность и поток. Температура поверхности равномерна и постоянна, равна°ТВт. Тепловой поток. Где верхний нулевой знак обозначает состояние непрерывности, t T равно Температура поверхности термоизоляции. Теперь, если поток газа разбавляется, а норма Рейнольдса остается постоянной, будет отображаться дополнительное сопротивление «Передача тепла скачком температуры. Это позволяет выразить общий коэффициент конвективного теплообмена, включающий как термический пограничный слой, так и сопротивление сопротивлению.
Скачок температуры, напишите: (10-42) 1 следующий скачок температуры можно записать как⁽1asas. Где^ _ и (dtldy) y ^ — температура и градиент температуры газового слоя Он непосредственно примыкает к поверхности. Величина; определяется по формуле (10-33), скачок температуры — это расстояние, которое происходит:5 = 1,996 2-a•Y, — p , И y + 1 Pr или =(10-44) условия скачка температуры, необходимо сначала r=/°.Ожидаемый q, то есть теплота, передаваемая между поверхностью и газом, одинакова с температурными скачками или без них.
Это на самом деле формула(10-43) ///₀ =Для группирующих уравнений (S-43), (10-41) и (10-42) получается true: затем подставляем в это уравнение значение B и получаем его по формуле (10-30) a⁰_ 。 bA⁰/ м ifupb2T-1⁻р-в РТП? T ’можно записать как Nu°_ 1 / — / M Nu°. Nu — ’ 1 ′ V 2 Re Pr (10-45)раствор (10-45) рассчитан для 2 атомарных газов、 если y = 1,4 и коэффициент аккомодации a = 0,8, то можно написать примерно так: чтобы воспользоваться формулой (10-45), нужно вычесть (тепло от шара Сплошная среда. Такое решение было получено путем грубой аппроксимации распределения скоростей вокруг шара[L. 174].Рассмотрим уравнение энергии сферы 10-13 системы координат игнорируют связь между системой сжатия и рассеянием механической энергии.
Сферическая система координат. Фигура 10-13: (’I + from i («»■S]•11М⁶ > в качестве приближения условия скольжения скорости, несмотря на симметрию«R = «φ = 0; = u 0df2_’i То же-направление ОО2-и следовательно, теплопроводность в направлении 0 сравнивается с конвективной формулой (10-46): (10-47) уравнение (10-47) может быть решено для граничного условия: t = t.\ R — > Sy преобразование Лапласа[L. 175]и дает средний коэффициент теплопередачи Критерий нусельта(1₊e -^) (1₊p») — ^ [/?( » .?) + Р? ( » .?[]? (10-48) где D-диаметр шара. = j / 2Re Pr; Л (ai I) И Л (ai₽i) — функции Бесселя. Представленное решение(10-48) Графически на рисунке M 0 в виде графика 10-14 и 10-15.Если мы рассмотрим решение (10-45) и (10-48) вместе, то получим результат, изображенный на рисунке.
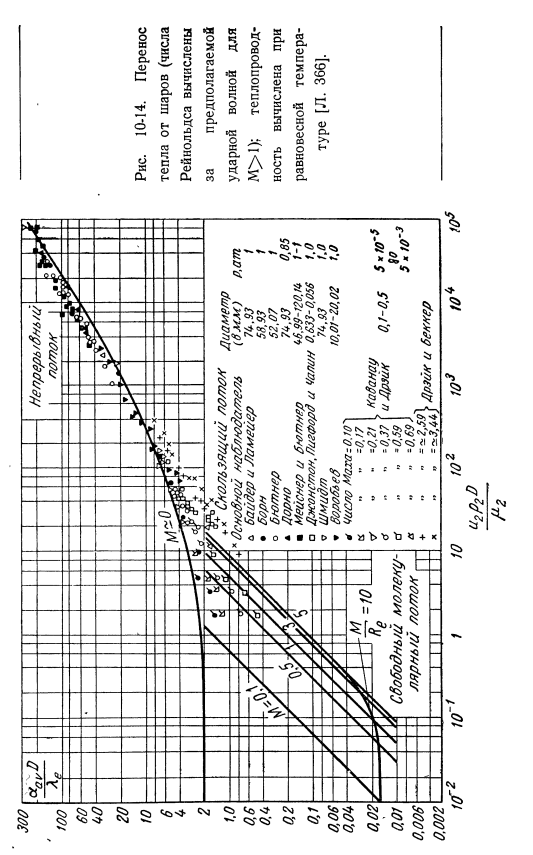
По сравнению с 10-15 Экспериментальные данные по теплопередаче для малых шариков. Константа решения (10-45) 2.59 была изменена эмпирически 3.42 для представления: Более точные экспериментальные данные: 1 4 3.42 (M / RePr) Nu° ’линии диаграммы 10-14 и 10-15 показывают передачу тепла в свободном молекулярном потоке. F. M. результаты расчета на основе кинетики по Sauer[L. [176]графические результаты показывают, что значения Рейнольдса Ноль через скорость или плотность. Если скорость теплопередачи шара равна нулю, радиальная теплопередача в неподвижном газе ограничена.
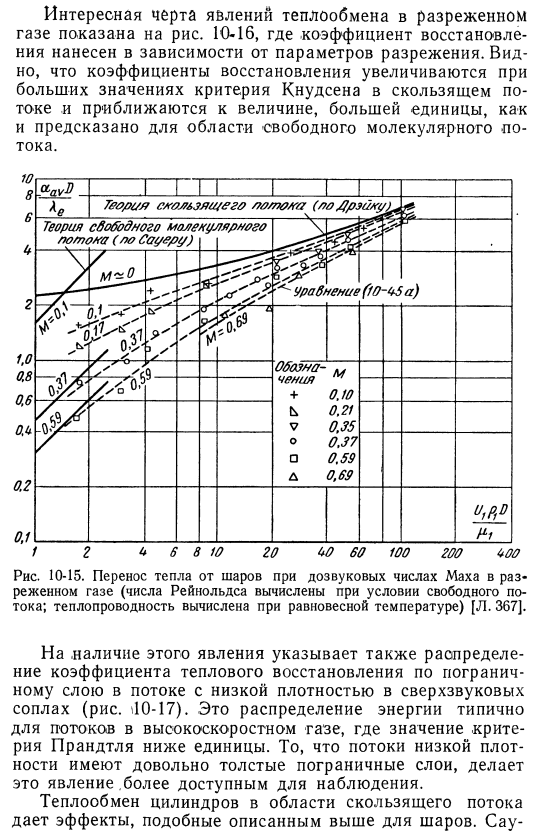
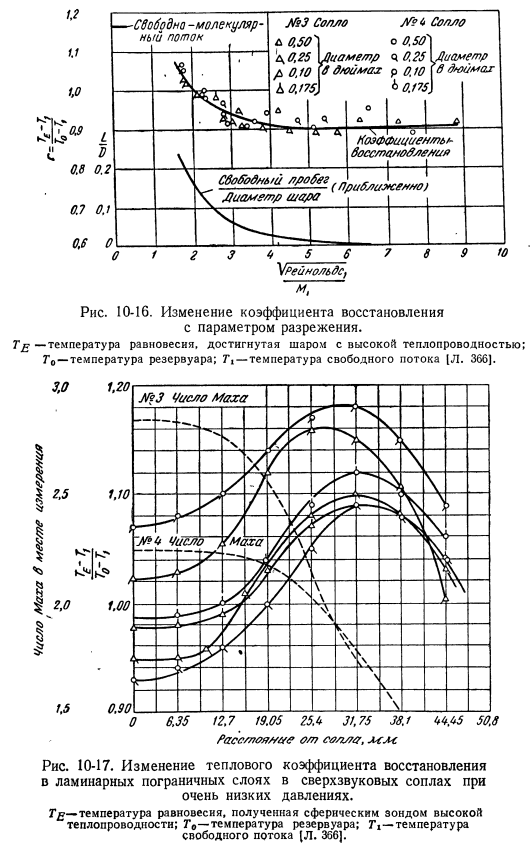
Время, когда плотность равна нулю, приводит к режиму свободного молекулярного потока и значительно более низкому коэффициенту теплопередачи. 300 ag o. y ig * 9 9 too 0.1 0.01 0.006 0.002 ″ ap2drg Рисунок S-14.Теплопередача от шара (число Рейнольдса вычисляется за предполагаемой ударной волной M> 1); теплопроводность вычисляется при равновесной температуре[L. 366].Я люблю эту игру. На рисунке показаны характеристики явления теплопередачи разреженного газа. На рис. 10-16 коэффициент восстановления строится в соответствии с параметром разбавления.
Коэффициенты являются По мере увеличения значения критерия Кнудсена в скользящем потоке скорость восстановления увеличивается и, как и предсказывалось в случае свободного, приближается к значению, большему единицы Молекулярный поток. Рис. 10-15.Теплопередача от шара при дозвуковом числе Маха в разреженном газе (число Рейнольдса, рассчитанное в условиях свободного течения; теплопроводность Рассчитано при равновесной температуре) [L. 367].О наличии этого явления свидетельствует также распределение коэффициента теплоотдачи по низкопоточному пограничному слою.
Плотность сверхзвукового сопла(рис. 40-17).Такое распределение энергии характерно для быстрых газовых потоков, где значение критерия Прандтля меньше 1.Струящиеся вещи Пограничный слой низкой плотности довольно толстый, поэтому это явление легко наблюдать. Передача тепла цилиндра в зоне сползая подачи эффективна. Как и в случае с вышеупомянутым шаром. Сан-10-16. измените коэффициент восстановления с помощью параметра разрежение. T E —равновесная температура, достигаемая высоким шаром Теплопроводность; это температура резервуара. T-температура свободного течения(L. 366].
Число Маха в положении измерения 10-17.Изменение коэффициента рекуперации тепла Сверхзвуковое сопло ламинарного пограничного слоя при очень низком давлении. Г£ — равновесная температура, полученная при высокой теплопроводности сферической probe. It это температура Резервуар; Ti-температура свободного течения[L. 356]. er (L. 177) распространяет свой анализ на цилиндр, а Стердер {L. 178]и другие получили экспериментальные данные о том же самом Интервальные переменные.
Свободные молекулы.’ Поток. Теплопередача Максвелла от тела к потоку благородных газов в равновесии может быть полностью рассчитана на основе: Из основных положений кинетической теории газа[л. 179-180].Результат может быть выражен в виде функции отношения y числа степеней свободы / числителя или удельной теплоемкости. Поскольку он непосредственно связан с/, результат всегда будет общим и будет рассмотрена молекулярная структура газа. Больше определения, чем показал Оппенгейм Соответствующие результаты нескольких основных форм, таких как плоская пластина, горизонтальный кольцевой цилиндр и шар, позволяют получить больше результатов .
Сложные случаи объединения результатов этих простых форм. Конвективный теплообмен объектов в свободном молекулярном потоке устанавливается на основе энергетического баланса. 7 = е — EP (10-49), где eᵣ= dER / dA-интенсивность молекулярного переноса энергии на единицу площади поверхности высвобождаемой молекулы. eₜ= Дейда-сила Передача энергии на единицу площади поверхности падающими молекулами. q-dQ / dA-коэффициент теплопередачи на единицу площади поверхности для потока газа. Опять энергия Она зависит от коэффициента регуляции высвобождаемых молекул а(см. формулу (10-34)).Из соотношения(10-34) и (10-49), это выглядит так:| =(10-50).
Она включает в себя поступательную энергию и часть внутренней энергии, связанной со свободой. Из принципа равного распределения энергии, внутренняя энергия молекулы газа с/ Степени свободы равновесного состояния при температуре T равны: k-постоянная Больцмана(k= 1.36-10 «1-10—。град-моль Дж энергии Поступательное движение молекул, выходящих из стенки при температуре T, равно e = 2n. внутренняя энергия поступательного движения молекулы распределяется на 3 Степени свободы; следовательно (10-51), где »» — это, как и прежде, число молекул, сталкивающихся с единицей. Площадь стены в единицу времени.
Передача энергии путем падать В случае молекулы, это выглядит так: е.= ₍ ₍+₀₀ > (10-52), где eₜ-поступательная энергия свободного потока, сталкивающегося с единичной площадью. Поверхность стены в единицу времени, и идти температура свободного течения. Подставляя в Формулу (10-50)соотношения(10-51) и (10-52), получим:| = Ts1pkTa,-(e / + Ts’pkt₀). (10-53) CP d [u + \ Wdt | 2’cᵥdufdt * / ’можно записать выражение (10-53) в функции y. — h + 277 ^ 1)» ■■(1⁰ -⁵⁴) где, y = 7₃ Соответствует одноатомному газу, а y = ⁷ / ₛ соответствует двухатомному gas. To рассчитав коэффициент теплоотдачи тела ot, нужно получить формулу для числа молекул n.
«Столкновение с единицей площади поверхности в единицу времени и энергией е transl поступательного движения. Эти значения предоставлены Oppenheim: n= — ^ [ ^ , + rM (14-erf₁ ₎)]; (10-55)Z U TS E,= [(^+v₂) n-ф ]₀уу (10-56), где n-число молекул на единицу объема. v-среднее значение Молекулярная скорость; = — компонент массового потока U, перпендикулярный стенке. s =(Y / y = ^ / y / 2M-отношение молекулярной скорости и числа Маха; = (LGU / 4 при подстановке вышеприведенных данных в уравнение (10-54) получается следующее безразмерное уравнение теплового потока. Q Y +1nLa I 1 V___________2 (у-1) dgththat I Y IjNvs’Nvs(10-57)для расчета теплопередачи объекта в свободном молекулярном потоке была определена следующая доля площади поверхности: J_ f-qO + erf t) I J 2s A, где A — Площадь поверхности образца.
Формула (10-57), интегрируемая областью A, может быть записана на основе следующего интеграла: (°+LLL2+ L>(G + O + yG.(10-58) передача тепла Свободный молекулярный поток может быть выражен критериями Стэнтона и коэффициентами рекуперации тепла. При Q = O формула(от 10 до 58) дает формулу температуры восстановления TW = стена в случае const. Это включает в себя тепловое сопротивление из-за теплопроводности в организме、 Конвекция газа на surface. In в этом случае= = 2 (^m) (^m+⁸, — T^) — ⁽1° — ⁵⁹ > теперь можно записать тепловой поток как функцию температуры восстановления Стена: Q = a (G + F) (Т» — Г) NkU, откуда определяется критерий Стэнтона, и далее Nk / p = /? — Газовая постоянная: Q-1 a (GF). (10-60) ст- 11___________________?CₚU(Tₐ-Tᵣ)ₜcₚU-2Т уравнения (10-27), критерий Прандтля Герольдсвиль, используя выражение вопрос._ Ню _ _ _ _ 9-Ф-5 Ну Ре РГ 4?
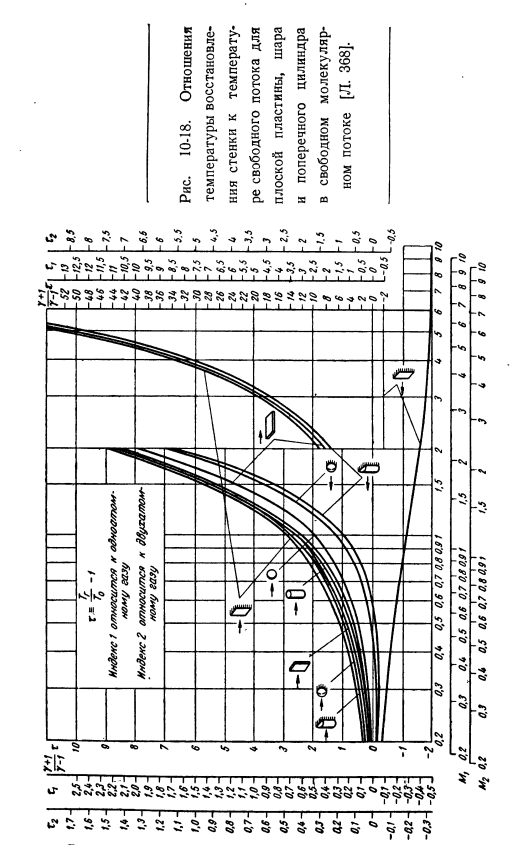
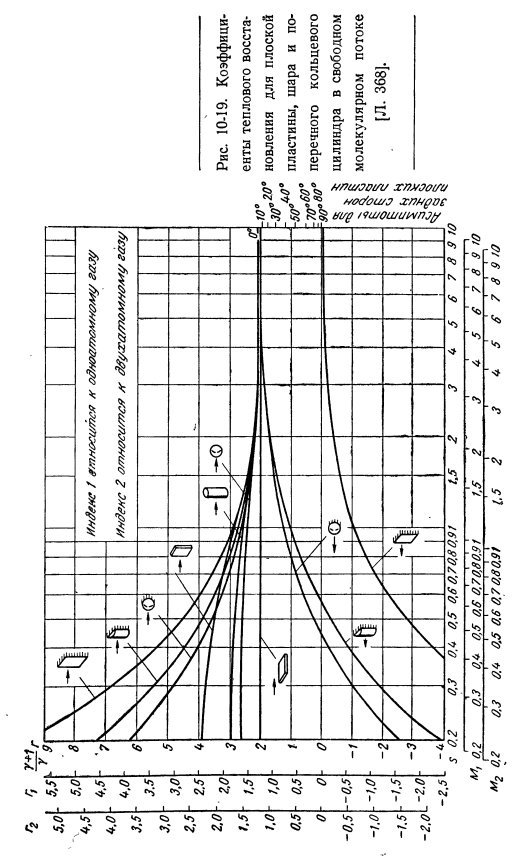
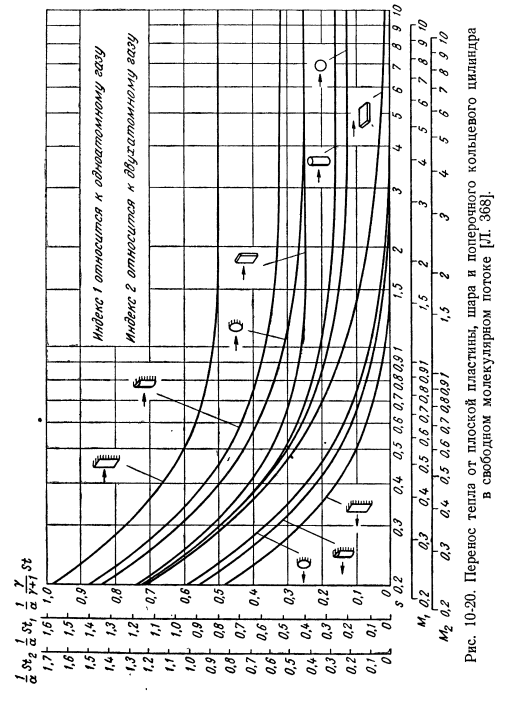
Коэффициент рекуперации тепла » Re » может быть выражен на основе формулы(10-59).— Тг-Тл(2+ УГ?) Стагнация температуры потока, стагнация потока относительно температуры потока может быть выражена как функция относительной скорости$:£= 1 + ^ M =1₊^ S. (10-61) коэффициент доставки Результаты, полученные на основе числителя (10-62) формулы(10-59)-(10-61), приведены в виде графика рисунка. 10-18-10-20.In дополнение к кривым, показанным на рисунке、 Другие кривые легко получить.
Например, плоская пластина-I 1.7- 1.6- 1.5- 1А.- 1.3- 1.2- 1.1- 1.0- 0.9- 0.8- 0.7- 0.6- 0.5- 0.8- QJ.- 0.2- 0.1- о-0.1—0.2 — — ой- f——- 1 —— 1–1 —- 1–1 —- r.-■; —- 1 —— g. m. 0.2 0.3 OS 0.5 0.6 0.7 0.80.91 1.5 2 i———- 1 — r-irnjrnm — — — — — — — — — — я—— 1—М₂0. 2 0.3 OS 0.5 0.6 0.7 08 091 1.5 2 10-18.Температура восстановления стенки и коэффициент температуры свободного течения плит, чаш и поперечных цилиндров в пределах свободных молекул Поток. 368]. М ’ ° ’ Г?-306 0.6 0.70.80.9}} ’、5 2′ J 4 5 6 7 8 9-1m2 0.2 0.8 0.9 0.5 0.6 0.70.80.9! 1.5 2 8 9 5 6 7 8 9 ю рисунок 10-19.Коэффициент термического восстановления плоской пластины, шара и кольцевого кольцевого цилиндра в свободном молекулярном потоке[L. 368]. (1 ″ Р—— 1 — 1-1-1 — 1-1-1-1-1 ——- Ф Я——- 1 — —!—— 1 -!Я −1 — — — 1 детьми 0.2 0.0 Обь 0.5 0.6 0.70.80.91 1.5 2 3 br / >в С 6 7 8 9 Ю Я — — — — — — Я — — — — — Я — — -!—— 1 — ИЖ— | —я ——- Я —- -Я ——- Я —- Я — 1–1 — я — я — IM₂0. 2 0.3 0.(4 0.5 0.6 0.7 0.80.91 1.5 2 3 0- 5 6 7 8 9 10 рисунок 10-20.Передача тепла от плоской пластины, шара и горизонтального кольцевого цилиндра в свободном состоянии[Л. 368].
Угол равен 0〜 Направление потока можно рассматривать в качестве примера (плоская пластина перпендикулярна потоку: и СеО) = 0j) sⁱⁿ⁰-здесь, 7] = ssin6.Символ 0 указывает на плоскую пластину、 Он расположен под углом к потоку, а символ n расположен на плоской пластине перпендикулярно потоку. Поэтому необходимо обратить внимание на: T₀ (s)=Stₙ (r|) sin b; re (s)=cos2⁶+ rn sⁱⁿ’fⁱ— Кроме того, что эффективный результат по отношению к плоской пластине применим к любой поверхности, образующей поток и определенный угол. Поэтому эти результаты применимы к клиньям и конусам、 Если угол наклона пластины соответствует половине решения клина или конуса angle. In в этом смысле плоская пластина с нулевым углом атаки похожа на цилиндр с произвольной боковой формой. Сечение осевого потока.
Смотрите также:
| Теплообмен при больших скоростях | Перенос тепла в жидких металлах |
| Перенос тепла в газах при высоких скоростях | Транспирация (просачивание через поры) и пленочное охлаждение |

