Оглавление:


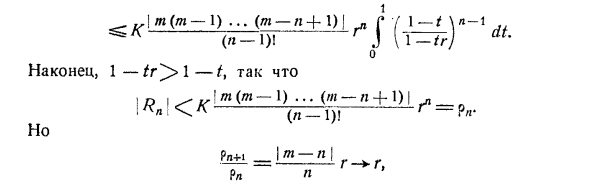
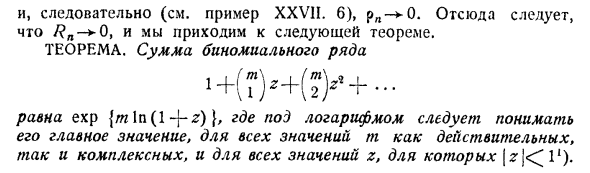
Общая форма биномиальной теоремы
- Общий вид биномиальной теоремы. У нас есть в общей сложности серии Равен (1 — \ — z) m = exp j m In (1 — \ — z)} для всех действительных значений m и z для всех действительных значений от -1 до 1. Когда указывает коэффициент Zn j w / l I _I t-n I 1 ! Я л + 1 Неважно, если это действительно сложно. Следовательно, ряд сходится для всех z, кроме модуля, меньшего 1 (см. Пример LXXX.3), и сумма равна exp {tn In (1 — \ — z) [т.е. основное значение (1 — \ — z) м. Из пункта 246, если t действительно: J-tzr = mz (l + tzy- \ Там, где z w t может быть действительным или комплексным значением, основные значения означают правую и левую части.
Таким образом, для c = (1 + tz) m: cp (n) (*) = m (, n-x) … (m-n + 1) r «(1 + tz) m до n. Людмила Фирмаль
| Логарифмический ряд | Дифференцирование функций от нескольких переменных |
| Некоторые приложения логарифмического ряда | Дифференцирование функции от двух переменных |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Эта формула также относится к / = 0, поэтому ‘n \’ \ n) Из соотношений (1) и (2) пункта 167 (с учетом замечаний, сделанных в конце пункта 170) где 1 Rn = J C-? (N> (0 <«■ о Put z = r (cos 6 + i sin G), m ~ / v, Найти верхний предел Rn. С другой стороны, l + fc | <2, С другой стороны 11 -f-tz (= / 1 + 2> rcos0-f ^ 1-tr ^ z 1-r и -r ^ am (1 плюс | (1 tz) m ~ l J = exp {(\ i-1) In) 1 — \ — tz \ -vam (1 -f-te)} = Первый элемент этого выражения не превышает if or (1-r) 1 * «1. Второй элемент В частности, [(1 — {- tz) m к x (верхняя поверхность не зависит от t (и η) \ (Fl 1 m (от m до x) (n «+ * * ‘AND» X о \ m (m- ) … (m- «+ 1) | -r 7 b- / ^ k ^ J 1 радж о
Поэтому (см. Пример XXVII.6): Когда мы достигаем следующей теоремы Теорема. Сумма биномиальных столбцов Равен exp \ m В (1 — \ — z). Где логарифм следует понимать как главное значение для всех значений m, как действительных, так и комплексных, а также для всех значений z в \ z \ <^ I1 —
Наконец-то 1-т P ^ I) … (m-i + 1) 1. ,Людмила Фирмаль

