Оглавление:




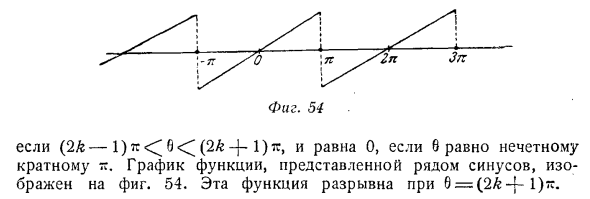
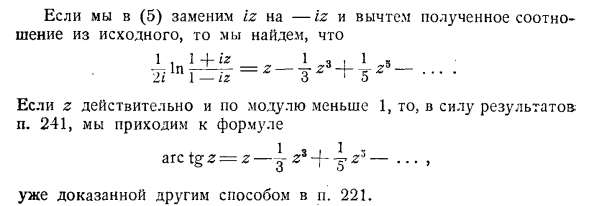
Логарифмический ряд
- Логарифмическая серия. В пункте 220 1р (1 =, (1) Где 0 является действительным и по модулю меньше 1. Поле справа будет абсолютно сходиться, если z — комплексное значение меньше 1. Естественно ожидать, что уравнение (1) будет справедливо для всех таких комплексных значений z. То, что это действительно так, может быть доказано с помощью выводов, аналогичных приведенным в §220. Кроме того, мы докажем, что (1) применимо ко всем значениям z.
«Можно предположить, что z не является действительным числом, потому что уравнение (1) уже доказано для действительного значения z. ^ = g (cos 6 + i sin 6) = C g, Вот так | rj ^ 1 и А = 1-Ф ц /, Далее опишите путь C, когда t увеличивается от 0 до g. Кроме того, G-G W J и Jl + Cf-о = / {c- «H- cv -… + (-1 V-.C — / — 1 dt = -r …… «> P, (и ‘,, n„ -1 <W «, o _ -ТП
Читатель говорит, что (1-yy) является основным значением Ln (1 4-z) Ми + 4-Д. Где C — отрезок прямой, соединяющий точки 1 и 1) -) — z в плоскости комплексной переменной. Людмила Фирмаль
FQ ^. (3) о Из неравенства (1). 170 с последующим г тмдт rrVf ^. (4) Но | l + t / | или | ~ | o> не меньше — длина перпендикуляра упала с 0 до линии C г ^ ! ^ m I ^ -J L // = (m + 1) (o + » о Следовательно, Rm- * 0 есть mc. Из (2) 1n (1 4-r) = r_1 +. (5) В процессе доказательства было показано, что ряды сходятся. Тем не менее, это было доказано ранее (LXXX, см. Пример 4). На самом деле ряды обязательно сходятся при \ z, Jz | = 1. Если z заменить на -z, 111 ^ = ^ 111 (1 = (6), 1, Zzjz 1. 245. Далее In (1 + ^) = 1n {(1 + rcos6) + / rsin6) = = 1 In (1 -f 2r cos 6-I-Г4) 4-1 arc, fsin9 .. ^ 1 л / л с 1 -j- g cos6 где Теперь нам нужно получить значение арктангенса. 1 1 р ,, между-2G и причиной себя «2G», 1 z является вектором, Выражается как интервал от -1 до g, а z находится внутри круга, главное значение am (1 -f 2) всегда находится между этими пределами. z | = 1 *).
Поскольку zm = r «1 (cos m6 + isin / yab), если действительная часть и мнимая часть сделаны равными в уравнениях (5) и 244, результат будет следующим. -i 1n (1 + 2rcose-fr-) = rcosO —-ir ° -cos26 + Lr3cos30— ■ …, arctg, G81 «9 g = rsin ^ sin 20+ i-r» sin 36 —…. ъ1 -} — rcosQ 2 1 3 Для Os ^ r ^ l эти уравнения содержат все значения 0, за исключением случаев, когда r = 1 и 6 равны нечетному кратному mc. Легко видеть, что это также относится к -1 ^, за исключением случаев, когда r = -1 и 6 равно четному кратному m. Особый интерес представляет р-1.
| Связь между логарифмической и обратными тригонометрическими функциями | Некоторые приложения логарифмического ряда |
| Степенной ряд для ехрz | Общая форма биномиальной теоремы |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- В этом случае In (1 + z) = In (1 + Cis 9) = i- In (2 + 2 cos 6) + i arc tg -y ^ — = = iln (-4cos, если -7: <^ 6 <^ 7r, поэтому cos 0- ^ cos 20 + ~ cos 36 —… = 4- In (4 cos? ~ 6), грех 0-й грех 20 + -и грех 36 -… = 6. Если другое значение равно 6, сумму этих рядов легко найти благодаря тому, что она является периодической функцией от 6 с периодом 2d. Таким образом, сумма нескольких косинусов iln (4cos * i b) Все значения 6 за исключением нечетных кратных k (ряд расходится при этих значениях), а сумма ряда синусов равна i (0-2 & tg)
Та же фигура. 54 (2k-1) π (2k-1 -1) r, равный 0, если 8 нечетно График функции, представленной серией синусов, показан на рисунке 2. 54. Эта функция прерывна с 6 = (2 ^ 4-1) -. Если вы замените iz на -iz в (5) и вычтете полученное отношение из исходного отношения, ± 1p = 2i 1-iz 3 ‘Y
Если 2 верно и по модулю меньше 1, это зависит от результата гл. 241 мы приходим на церемонию 1 3. 1 л дуга igz = z — y2. «5t2 ‘- •••» уже доказано другим способом в разделе 221. Людмила Фирмаль

