Оглавление:

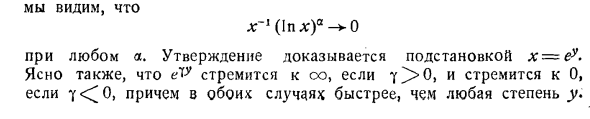

Основные свойства показательной функции
- Основные свойства показательной функции. (1) Если x = ey} и y = 1pl, dv _ 1 dx _ _ y дх ~~~ ху- Таким образом, производная экспоненциальной функции равна самой функции. В общем J-ea ”= ау. Dy (2) Экспоненциальная функция удовлетворяет функциональному уравнению f (y + z) = f (y) f (z) — Для рационального y n z это видно из нормальных правил. Если y и / или z невозможно, вы можете выбрать две последовательности рациональных чисел yv _y2> …, yn> …. И zv z2 ….. zn, … liu „= y и Umzn = z, то в силу Экспоненциальная непрерывность eu e * = lim eVfl • Hm * lim + * n =: ey + z.
В частности, от e до y = e ° = l или от e до y = -to-. Людмила Фирмаль
| Число е | Представление е в виде предела |
| Показательная функция | Обыкновенные логарифмы |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
Вы также можете вывести это функциональное уравнение из функционального уравнения \ nx. yx = In xv = In xb1, x1 = eY1, xr-eY *, yx + y2 = 1n xy + In x ^ = In xtxv и eY \ + Y * = ein * ix * -Xlx2 = eY * -eYy. (3) Функция ey становится бесконечной, если y увеличивается быстрее, чем порядок y. lim = \ woo ~ y = 0 уоо для всех сколь угодно больших значений Идентифицирован х LGR В х 0 с положительным а. предположение Мы видим это x’1 (\ nx) a ^ 0 Любое утверждение доказывается заменой x ~ e? Это Эль? Если есть тенденция к О, если есть тенденция к О, Если 7 <^ 0, оба быстрее, чем степень y.
Из этого результата мы можем построить «шкалу порядка роста», подобную той, которая была построена в §210, но простирающейся в разных направлениях. То есть масштаб функции, которая увеличивает k на x. Эта шкала представляет собой ряд функций. X, X \ X *, … t 6xj. •. 6х. ••, ф. • 6е. , , , Здесь, конечно, вам нужно понимать e {x * \ …, \ … с ex, e **, …. Читателям рекомендуется перенести замечания, сделанные в пункте 210, и пример LXXXV «логарифмическая шкала» в эту «экспоненциальную шкалу».
Конечно, вы можете объединить обе шкалы в одну. После: …, In In x, …, In x, …, x, …, она * 9 …. Людмила Фирмаль

