Оглавление:

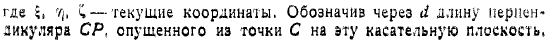




Устойчивость равновесия
Задача устойчивости равновесного состояния рассматривается только применительно к вытеснению плавающего тела из равновесного состояния при сохранении объема гидромеханики, погруженного в жидкость. Такие движения сводятся к вращению тела вокруг горизонтальной оси, которая, как указано, находится в плоскости навигации и проходит через центр инерции в зоне навигации. Вопрос об устойчивости равновесия по отношению к различным видам смещений очевиден.
Потому что, по отношению к любому вертикальному перемещению перевода, равновесие всегда вертикально к любому горизонтальному подходу, и отношение к любому вращению. Является более устойчивым для реальных перемещений, но вокруг вертикальной оси равновесие плавающего тела становится безразличным. Принимая во внимание стабильность равновесия при вытеснении, которая не изменяет объем вытесняемой жидкости, она принимает примерно одинаковое значение.
С объемом гравитацией, погруженной в жидкость, и осью вертикально вверх. Тогда радиусы кривизны главных нормальных сечений поверхности центров в равновесном состоянии тела плоскость касается центральной поверхности, координаты центра тяжести всего тела будут равны. Возьмем точку, близкую к центральной поверхности, проведем касательную плоскость к ней.
В состоянии равновесия тело находится в покое (вектор скорости равен нулю) в выбранной системе отсчета либо движется равномерно прямолинейно или вращается без касательного ускорения. Людмила Фирмаль
Исходя из этого уравнения, текущая координата указывает длину вертикали и опускает от точки до этой касательной плоскости. Мы, в соответствии с известной формулой аналитической геометрии, выглядим так: в ряд, умножая далее. Сохраните минимальный минимальный срок заказа по отношению к малым количествам; и используйте формулу, находите последовательно. Разложение фактора теперь критерий Дирихле, определяющий устойчивость равновесия, достаточен для минимизации потенциала силы, приложенной к телу в положении равновесия, чтобы стабилизировать равновесие тела.
Они сводятся к телу и сводятся к вертикальным силам: сила веса, приложенная к точке и действующая вниз, и результирующая сила гидростатического давления, приложенная к центру тяжести погруженного объема и действующая вверх; при равновесии тела и равенстве сохраняется при движении после центра, если вертикальные координаты точек указаны после, т. е. потенциальные силы, приложенные радиусы к телу, когда установившееся движение ось направлена вверх, выражаются из механики, известной уравнениями или формулами, известная формула аналитической геометрии. Чтобы найти следующее, используя минимальный минимальный срок заказа для небольшого числа; формула.
Механическое равновесие — состояние системы, при котором её положение в конфигурационном пространстве находится в точке с нулевым градиентом потенциальной энергии. Людмила Фирмаль

