Оглавление:

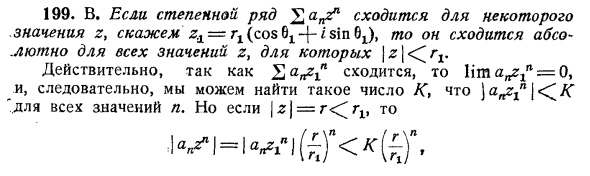

Степенные ряды
- Степенные ряды. Одной из наиболее важных частей теории простых элементарных функций (синус, косинус, логарифмическая, экспоненциальная и т. Д.) Является разложение в ряд форм. Такой ряд называется степенным рядом по x. В связи с сериями Тейлора и Маклаурина мы уже встречали несколько расширений этого типа серий (см. Пункт 152). Однако учитывалась только фактическая переменная x. Здесь мы рассмотрим некоторые общие свойства степенных рядов относительно z. z — комплексная переменная. A.
Достаточно привести один пример для каждого случая. Vj ZN 1. Ряды / сходятся для всех значений r. Zn , Nta = n I фр. 11 I * 1 l I un I P + 1 ‘ Каким бы ни было значение r, результатом является то, что в соответствии с критериями Даламбара оно сходится ко всем значениям z, а начальный ряд полностью сходится ко всем значениям r. После этого, когда степенные ряды сходятся, вы можете видеть, что они обычно сходятся полностью. 2.
Степенной ряд V a ^ может сходиться без какого-либо значения z или только значений из определенной области, или без значения Z, кроме Z-0. Людмила Фирмаль
За исключением 2 = 0, ряд не сходится для значений z. Это un ~ n \ zn имеет тенденцию быть oo подобным η-> oo, когда ψ0. В результате (пример XXVII, см. 1, 2, 5) модуль n-го члена ряда имеет тенденцию быть ω (при η — ► ° °). Таким образом, последовательность ue может сходиться без значения r, кроме 0. Также ясно, что степенной ряд сходится, когда 2 = 0. 3. Серия 2 сходится для всех зр. z | <1, который расходится для всех zys в jz. Это было доказано в разделе 88. Таким образом, есть примеры каждого из трех возможных случаев.
Б. Степенные ряды сходятся Значения z, например ^ = rx (потому что Bjl — {- sin sin 6X), абсолютно сходятся для всех значений z в \ z \ <rv Фактически, поскольку 2 Vi сходится, lim a ^ * = 0, поэтому вы можете найти такие числа, как «z» для всех значений r, но \ z \ = r <^ тогда fr \ n f r \ n t) <x [t) •
| Признаки сходимости Абеля и Дирихле | Область сходимости степенного ряда. Круг сходимости |
| Ряды с комплекснымй членами | Однозначность степенного ряда |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Утверждение сходящейся геометрии (г \ п Прогресс. То есть, если ряд сходится в точке P, он полностью сходится во всех точках ближе к началу координат, чем P. Пример. Показано, что утверждение остается в силе, даже если ряд колеблется при z = zx. [Если „= q0 4-4-4- … 4″ anz «>, то | sn [<K для всех значений n, где i Vl «i = \ Sn- | ^ | 5H; 4- | S /] _ i i: <2к
И доказательство заканчивается как основной случай. Людмила Фирмаль

