Второе достаточное условие экстремума

Второе достаточное условие экстремума

• Второе достаточное условие экстремума. Это 7.2. Тогда функция f (x) имеет локальный максимум/(2) (C)<0, если / (2>(C)>0 в точке C. D o K a z a t e l s T V o. из теоремы 6.1, доказанной в условиях/<2>(C)<0 (>0) и главы 6.1, функция f'(x) уменьшается (увеличивается) в точке C. Рис 7.3 Существует такая окрестность точек C, в которой f'(x)

положительно (отрицательно) находится слева от C, а отрицательно (положительно) — справа от C. Теорема 7.2, вообще говоря, имеет более узкий диапазон, чем теорема 7.1. Таким образом, теорема 7. 2

не решает проблему экстремальных значений, если квадратичная Людмила Фирмаль

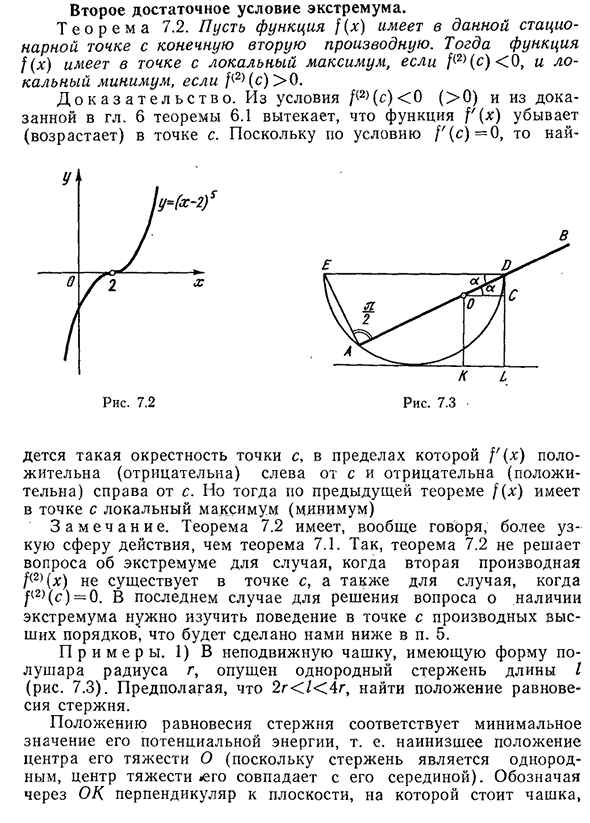
производная/(2) (x) отсутствует в C, или^2) (C)= = 0. В последнем случае для решения задачи о существовании экстремумов необходимо изучить поведение в точке с производных более высокого порядка, что и будет выполнено далее в пункте 5. П р и М е ч а н и Е. 1) в неподвижную чашку с полусферической формой радиуса G

опускается однородный стержень длины I (рис.7.3). 2G < / < предполагая 4G, найти положение равновесия стержня. Положение равновесия стержня указывает на минимальное значение его потенциальной энергии, то есть на самое низкое положение его центра тяжести, 266 ч, через ОК перпендикулярно его центру и

• плоскости, на которой стоит одна чашка, так как стержень однороден. 7. Рассмотрим график функции Сводим задачу к нахождению положения стержня АВ, где ОК отрезка имеет минимальную длину. Во-первых, в зависимости от угла a угла наклона стержня относительно плоскости, на которой стоит чашка, вычисляют длину

сегмента OK. Сделайте прямую линию DL параллельной линии OK, а прямую линию OS перпендикулярной OK (D-точка, в которой стержень находится на краю чашки). Из соображений правильного треугольника ЕАД, ад-Эд, потому что а=2р потому что. Так 0d уровень-АД-АО=2р потому что—- -— Два. Это следует, С другой стороны, DC=DL-OK-g-OK. Итак, если мы рассмотрим прямоугольный треугольник ODC, то Грех а DC_g-OK0D » г 2Р потому что—2 Таким образом, длина сегмента OK, представляющего f (a), будет равна

Мы переходим к поиску значения угла a, которое обеспечивает минимальное Людмила Фирмаль

значение yes). (Понятно, что мы можем ограничиться величиной угла а с первой четверти.) F'(a)== — cos a-2r cos2a= — cos a+2G-4r cos2a так как стационарная точка была найдена как решение квадратного уравнения 4Р cos2a — — — — — потому что-2Г=0. Два. Так как cos a в первом квартале положителен, то для нас подходят только положительные корни этого уравнения потому что А0 1+г? +128g2 _16g (7-2)) С точки зрения задачи ясно, что единственной стационарной точкой АО

является минимальная точка функции Da), но это строго установлено теоремой 7.2. Достаточно убедиться, что/(2) (AO)>0. Потому что/(2>(а)= — — — — — грех+грех 4Р 2А=поэтому 8R грех»(потому что—- 1— \ , 2\16g / §1. Найти стационарную точку 267 Тогда(7.2) / {2>(a)=8r sin a0cos A0 128r2>0. Таким образом, установлено, что равновесное положение стержня соответствует углу наклона к плоскости, на которой стоит чашка, определяемому по формуле (7.2). 2) снова найти точку

exrtemum функции f (x)==X3-X2-4. Стационарными точками этой функции, как было показано выше, являются точки x=0 и x=2. FW (x)=6x-6 so f(2)(0)=— 6<0, f(2)(2)=6>0, тогда, благодаря теореме 7.2, функция f (x) имеет максимум в точке 0 и минимум в точке 2. Экстремумы этой функции fmax=f(0)=-4, fmin=f (2)=-8.

Смотрите также:

Методическое пособие по математическому анализу

Первое достаточное условие экстремума	Геометрический смысл производной.
Определение производной	Первообразная