Оглавление:


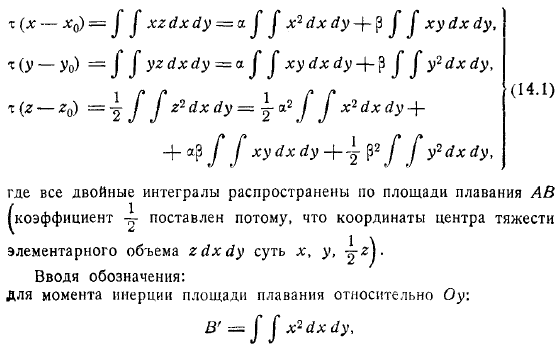

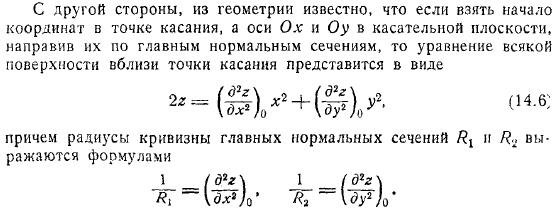


Радиусы кривизны главных нормальных сечений поверхности центров
Фиксируем некоторую плоскость плавания и проведем в ней оси, взяв начало координат в центре инерции площади плавания; соответствующее положение центра тяжести погруженного объема обозначим через с координатами проведем другую плоскость плавания близкую к, и отметим соответствующий ей центр с координатами. Положительную ось будем считать направленной вертикально вверх. Уравнение плоскости гидромеханики может быть написано в виде, так как при получаем — уравнение плоскости.
Для определения координат точек на поверхности центров служат известные формулы. Отсюда находим: причем последние интегралы распространены только на клиновидный объем между плоскостями. Выражая элемент этого последнего объема через, где координата переменной точки плоскости, мы приведем последние формулы к виду, где все двойные интегралы распространены по площади плавания коэффициент поверхности центров поставлен потому, что координаты центра тяжести элементарного объема.
Вводя обозначения: для момента инерции площади плавания относительно: для момента инерции площади плавания относительно: для центробежного момента. Перепишем предыдущие формулы в виде. Откуда, решая первые два уравнения относительно и подставляя в третье, получаем уравнение поверхности центров по соседству с точкой.
Обычно кривизна определяется для каждой точки на «объекте» и выражается как значение некоторого дифференциального выражения 2-го порядка. Людмила Фирмаль
Последнее уравнение упрощается, если за оси взять главные оси инерции площади плавания; тогда, как известно, будет превратятся в главные моменты инерции, и уравнение примет вид центров. Если, наконец, при сохранении направления осей перевести начало координат в точку, то уравнение поверхности центров еще более упростится и примет вид.
С другой стороны, из геометрии известно, что если взять начало координат в точке касания, а оси в касательной плоскости, направив их по главным нормальным сечениям, то уравнение всякой поверхности вблизи точки касания представится в виде причем радиусы кривизны главных нормальных сечений выражаются формулами.
Сравнивая уравнения ,приходим к заключению: что главные нормальные сечения поверхности центров параллельны главным осям инерции площади плавания, соответствующей точке касания; что радиусы кривизны главных нормальных сечений устойчивости равновесия связаны с главными моментами инерции площади плавания простыми соотношениями.
Иногда кривизна определяется в интегральном смысле, например, как мера, такие определения используют для «объектов» пониженной гладкости. Людмила Фирмаль

