Оглавление:



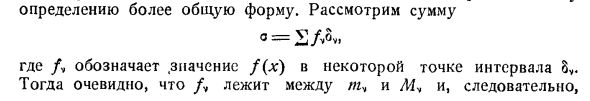

Определенные интегралы и площади
- Определяется интеграл и площадь. В пункте 148 гл. VI Если / (hp) является непрерывной функцией от x и of, то Я является дугой графа / 0 * 0, и область, окруженная PrP с ординатой P1M1 и PN и сегментом оси X NXN, равна Принято, что может быть связано с определенным числом, называемым ON = x, когда x изменяется, ясно, что эта область будет функцией x, обозначенной F (x). С этим предположением § 148 доказывает, что F ‘() = / ()>, и показывает, как применить этот результат к вычислению площади нескольких областей, окруженных кривой.
Я знаю, что означает площадь прямоугольника и что она измеряется произведением длины сторон прямоугольника. Свойства треугольников, параллелограммов и многоугольников, доказанные Евклидом, дают нам возможность определить площадь этих фигур. Однако то, что нам известно до сих пор, напрямую не определяет площадь фигуры, ограниченную кривой.
Это было Однако нам все еще нужно доказать основное предположение о том, что величина F (l;) — область этой фигуры — действительно существует. Людмила Фирмаль
Вот как можно определить F (x), чтобы мы могли доказать существование этого числа. Предполагая, что f (x) непрерывна в замкнутом интервале (a, b), разделите этот интервал на несколько подинтервалов, разделив точки xb, xv …, xn.Выразите интервал как ov, а точный нижний предел — как t Лицо (см. §103) f (x) в и положить s = t0 o0 + w181 + … + «i-A-i = Если является точной верхней границей f (x) в (a, b), то ясно, что это sМM (b-a). Поэтому набор значений для s ограничен выше (см. §103) и имеет точный верхний предел.
Одно значение s никогда не превышает y, но есть значение для s, которое больше любого числа меньше, чем y. Точно так же, если M- указывает точный верхний предел f (x), установите S = 2AUK S <m (b-a), где m — точная нижняя граница функции f (x) в (a, b). Таким образом, набор из 5 значений имеет точную нижнюю границу, обозначенную J, и является нижней границей. Значение 5 будет не меньше Y, но значение 5 будет меньше любого числа больше J. В простом случае, когда f (x) монотонно возрастает при (a, b), полезно понять геометрический смысл сумм s и 5. B // fv = / (* v) в этом случае И Afv -f «) •
| Теорема о среднем для функций от двух переменных | Определенный интеграл |
| Дифференциалы | Площадь сектора круга. Круговые функции |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Всего Общая площадь прямоугольника, заштрихованного на фиг. 44 и 5 областей фигуры окружены жирными линиями. В общем случае s и 5 также являются областями фигуры, состоящей из прямоугольников, а s является областью такой фигуры, которая полностью содержится в изогнутой фигуре, и является определяющей областью, а 5 представляет собой Область, которая содержит эту последнюю форму. Где значение одного k, N ‘$ Та же фигура. 44. Генерация единственного значения S. s и S — суммы, соответствующие одному разбиению интервала, а s \ S ‘- сумма, соответствующая другому разбиению. s ‘^ S должен отображаться. Вы можете сформировать третий раздел ноги. Все точки s и S считаются точками деления.
В случае s \ S ‘s и S указывают сумму, соответствующую этому третьему разделу. Тогда это легко увидеть s ^ s, s ^ s’y S ^ vS «(1) \ v ….. \ pt Член m \ bF из s заменяется суммой на s Где mM, ffht% t … указывает точную нижнюю границу f (x) в 8M8v> it, но m ^^ / и, … … Сумма больше, чем mySv. Таким образом, s ^ s и другие неравенства (1) могут быть установлены таким же образом. Но поскольку s ^ S, это выглядит так: Если вам нужно доказать.
Например, s отличается от s, и, по крайней мере, один интервал в s делится на fia через несколько меньших интервалов Людмила Фирмаль
Действительно, мы можем найти Значение S произвольно близко к значению S, сколь угодно близко к J 1)> До сих пор мы не использовали f (x) непрерывность. Покажем, что если число точек разбиения x увеличивается бесконечно, так что все интервалы 8V стремятся к нулю, j-J и сумма s и 5 стремятся к пределу J . Точнее, мы можем найти 8 для любого положительного числа е. O ^ Y — s > как требуется Для отображения. Определите область N ^ NPPX как общее ограничение s и S. Другими словами, используйте номер J для этой области.
Определите более общую форму. Учитывайте сумму Где / v указывает значение f (x) в определенный интервал времени ov. Тогда ясно, что / v находится между rm и AU. Таким образом,Если интервал 8V стремится к нулю, o становится пределом J. Таким образом, площадь может быть определена как предел общего o.

