Оглавление:

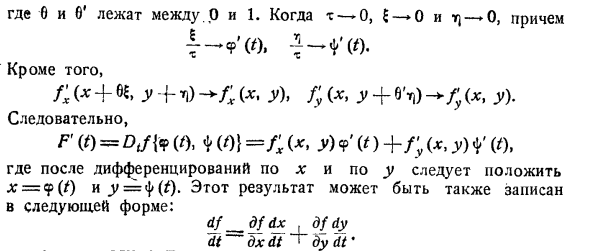
Дифференцирование функции от двух переменных
- Дифференцирование функции двух переменных. Существует одна теорема, связанная с дифференцированием функций от одной переменной. Это играет очень важную роль, но опирается на концепцию частичной дифференциации, описанную в предыдущем разделе.
- Дает правила дифференцирования по t-функции / {9 (0> «Во-первых, f (x, y) является функцией двух переменных x и y, а / j и fy являются непрерывными функциями x и y (см. 108)
Это так называемая совершенная дифференциальная теорема. Людмила Фирмаль
Предположим, что для всех значений этих переменных изменение x и y ограничено тем фактом, что точка (x, y) должна находиться на кривой. Где φ и ty — функции t с непрерывными дифференциалами qp ‘(/) и φ’ (0 * Т °.
| Дифференцирование функций от нескольких переменных | Теорема о среднем для функций от двух переменных |
| Общая форма биномиальной теоремы | Дифференциалы |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Где f (, y) — функция одной переменной t, например F ( сводится к т) F ‘(т). Предположим, что t изменяется от t до x и Y изменяется И — (- YJ. Тогда по определению [/ {? (<+ «). ♦ (<+»)} — L «Ю. ♦ ()}! -g— «0 = lim 1 {f (x + (, y + Tj) -f (x, y)} = f (x + i, y + D-f (x, y + rd. _ {J (x, y + yd-fjx, y) t h] С L S X ‘>] — J Однако согласно теореме о среднем значении _y-j- B’ti),
Где 0 и O находятся между O и 1. для х-о и р-о, и T также /; (X + b y + rd- + rx <. Y), /; (, .y + 8’ij) (*, l. так f (o = (o. * w} = /; (. l 9 ‘) + /; <, y) f (o. Здесь после дифференцирования по * и j / нам нужно положить jc = 9 (/) и _y = φ (/).
Результат также может быть записан в следующем формате: df _dfdx __d) fdy dt dxdt 1 день Людмила Фирмаль

