Оглавление:





Точные решения уравнения энергии ламинарного пограничного слоя
- Температурное поле вблизи плоской пластины и связанный с ним теплообмен также рассчитываются по точному решению уравнения пограничного слоя для двумерного стационарного течения. Раствор пластины с постоянной температурой поверхности был сформирован в 1921 году в e. pollhausen [l. 78]. Он предположил, что члены уравнений, представляющих вязкое рассеяние, не учитываются в уравнениях энергии пограничного слоя, поскольку скорость потока достаточно мала.
Форма этого уравнения выглядит следующим образом: ДТ, ДТ Д4 Связанные граничные условия : при r / = 0 при г = ОО § 6 показывает, что в особых случаях уравнение пограничного слоя может быть преобразовано в полный дифференциал Социальное уравнение с введением следующих новых переменных: Эти же переменные вводятся в приведенные выше уравнения энергии, а затем вводится следующий безразмерный параметр, описывающий температуру внутри пограничного слоя: В результате получаем уравнение Граничное условие для 7)= 0、6 ’= 0、для t | = ОО, 6 ′ = 1. Это уравнение может быть интегрировано таким же образом, как и уравнение (6-44). : (7-24).
Таким образом, вводимое в феноменологической термодинамике количество теплоты может быть измерено посредством калориметрического тела (об изменении внутренней энергии которого можно судить по показанию соответствующего макроскопического прибора). Людмила Фирмаль
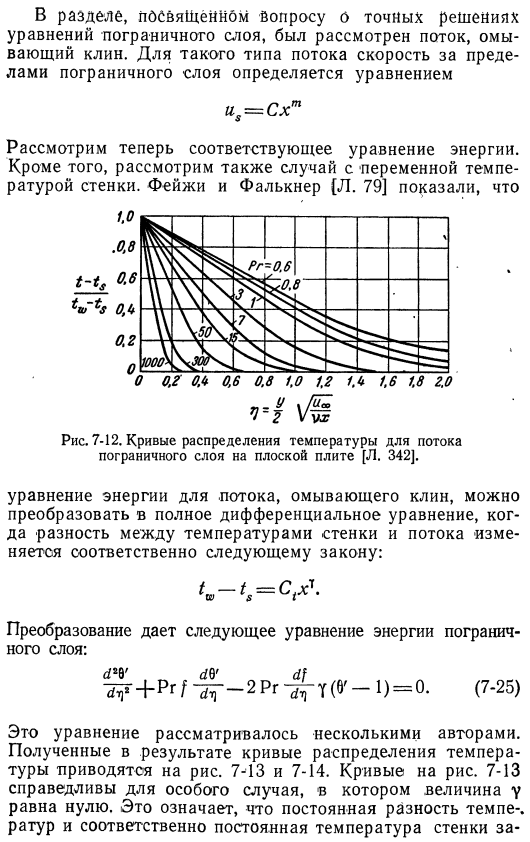
В этом случае f следует считать известной функцией, а формула (7-24) является точным решением формулы (7-23). Кривая распределения температуры, полученная таким образом, показана на рисунке. 7-12 для различных значений эталонного pr. Коэффициент теплопередачи равен、 по ’nux = f (pr) j /’ re ^. E. В диапазоне чисел Прандтля от 0, 6 до 15 параметры / (pr), рассчитанные порхаузеном, могут быть выражены с достаточной точностью с помощью зависимостей. Ф (пр) = 0. 332 ^ П? В разделе, посвященном вопросу точного решения уравнений пограничных слоев, рассматривалась промывка клина.
Для этого типа течения внешняя скорость пограничного слоя определяется следующим уравнением: uₛ= Цефуроксиму Далее рассмотрим соответствующую энергию equation. In кроме того, он также учитывается при изменении температуры стенки. Фейге и Фолкнер (л. 79) 、 Рис. 7-12. Кривая распределения температуры граничного ламинарного потока на плоской пластине[l. 342]. Уравнение энергии потока для промывки клина может быть преобразовано в полное дифференциальное уравнение, если разница между температурой стенки и температурой потока изменяется по следующему закону.
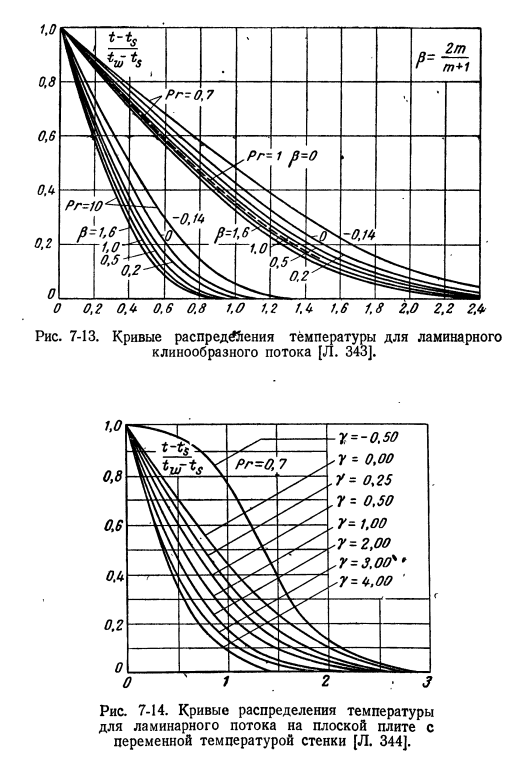
- Преобразование дает следующее выражение энергии пограничного слоя: d28’dw ДФ. + Пр ф ш-2 пр Г (О ’ −1) = 0 (7-25). Это уравнение рассматривается более чем одним автором. Полученная кривая распределения температуры показана на рисунке. 743 и 7-14. Кривая 7-13 рисунка справедлива только в особых случаях, когда величина y равна нулю. Это связано с постоянной разницей в температуре, температуре и, следовательно, постоянной температуре стен 1, 0. Рис. 7-13.
Ламинарная клиновидная кривая распределения температуры потока[l. 343]. Рисунок 7-14. Кривая распределения температуры ламинарного потока на плоской пластине, температура стенки которой изменяется[l. 344]. Ранее установленный. Параметры 0 = 2 /и/ (/и+), описывающие особые условия течения на кривой распределения температуры; 1) воздействие не столь велико, особенно в сравнении с воздействием на кривую распределения скорости. На рис. 7-14, С другой стороны, показана кривая распределения температуры потока по плоской пластине (0 = 0) при изменении температуры стенки (в соответствии с различными значениями y).
Интересная ситуация возникает, когда значение y отрицательно. Людмила Фирмаль
Изменение температуры стенки оказывает большее влияние на кривую распределения температуры, чем изменение расхода. Кривая распределения температуры имеет вид буквы s, а градиент температуры стенки (отсюда и тепловой поток стенки) может быть нулевым или даже отрицательным (при y −0, 5). Это означает, что даже если локальная температура стенки выше температуры потока, этот частный случай может привести к ситуации, когда поток тепла направляется от потока стиральной машины к стене.
Этот довольно странный факт можно объяснить следующим образом. Отрицательное значение y означает, что температура стенки падает в направлении flow. As в результате жидкие или газовые массы из области чуть выше стены вступают в контакт с более горячими стенами, а стены проходят через более холодные. Они несут эту температуру вниз по течению, в результате чего поток стены будет горячее, чем стена itself. In в конце концов, такая ситуация вызывает обратный тепловой поток от жидкости к стенке. Изменение температуры стенки (y = −0. 5).
Мы рассчитаем это и покажем на диаграмме. 7-14 кривую распределения температуры трудно воспроизвести экспериментально, поскольку температура на переднем конце стенки должна быть бесконечно высокой. Однако мы обнаружили, что инверсия температурного профиля и теплового потока качественно проявляется и в других законах изменения температуры стенки. Например, такими случаями являются Чепман и Рубесин [l. 80], а также Шлихтинг [l. 81] позиция, аналогичная позиции, показанной на рисунке. — y = 0, 5 из 7-14 возникает при охлаждении film. At на этот раз пленка охладителя распыляется в поток при x = 0.
Холодный пограничный слой созданный охладителем делает поверхность плиты Горячая жидкость или газ в потоке. Поскольку пограничный слой нагревается от потока за счет теплопроводности, этот эффект уменьшается вдоль потока.
Смотрите также:
| Плоская пластина с произвольно изменяющейся температурой поверхности | Движение жидкости в трубе |
| Поперечное омывание цилиндрических тел | Аналогия между количеством движения и теплообменом |

