Оглавление:






Плоская пластина с произвольно изменяющейся температурой поверхности
- В предыдущем разделе мы исследовали случай, когда температура tₛ x₀ составляла x =x₀ ТВт twtherefore, температура стенок меняется в несколько этапов вдоль пластин. В этой технике важны и другие типы изменения температуры стенок. Для некоторых из них Чепман и М. В. Рубезин интегрировали дифференциальные уравнения пограничного слоя [l. [71].
В таких случаях он также может быть рассчитан с использованием метода, описанного в предыдущем пункте. Изменение температуры поверхности вдоль оси x оказывает двойное влияние на температуру границы layer. It влияет на форму кривой распределения температуры и толщину пограничного слоя. Первый эффект дифференцируется относительно y, без члена, для которого формула (7-5) оценивает рассеяние, и становится заметным, если y = 0.
Тогда оно не способно совершать макроскопическую работу, но может обмениваться энергией (то есть теплотой) с телом {\displaystyle X}X. Людмила Фирмаль
Результат этого расчета、 ₌/ делать_ ду) г = с dx• Это уравнение выражает связь между 3-й производной кривой распределения температуры и градиентом температуры стенки. Используйте его снова для определения констант принятого уравнения и аппроксимации распределения температуры curve. In кроме того, разность температур o теперь является функцией x, которая должна оставаться в самом дифференциальном операторе d / dx в формуле на стр. 221. Другой метод расчета основан на том, что уравнение энергии (7-5) является линейной производной. * Данное уравнение дает решение температурного поля с произвольными изменениями температуры стенки.
Это можно рассматривать как большое количество ступенчатых изменений. Этот метод обычно называют теоремой Дюамеля (1833) и часто используется для анализа электрических circuits. As решение этой задачи этот метод впервые был применен в предложениях, выдвинутых М. В. Рубезиным в 1945 году. Эти положения очень удобны и соответствуют не только плоской пластине постоянной скорости и$, но и объектам различной формы, а также ламинарным и турбулентным состояниям. Формула (7-5) представляет собой линейное дифференциальное уравнение, представляющее температурное поле t в пограничном слое.
Предположим, что для конкретного граничного условия существуют некоторые конкретные решения этого уравнения, ti. Затем, подставляя в Формулу (7-5) выражение 1. Это тоже его решение. Константа cz может быть использована для адаптации нового решения к требуемым граничным условиям. Тепловой поток на поверхности выглядит так: ’=Х (4). — 1. Предположим, что каждому конкретному решению соответствует условие, при котором температура стенки равна температуре потока в определенном месте и затем резко изменяется на температуру twₗ.
Для каждого конкретного решения коэффициент теплопередачи можно определить из уравнения Где температура стены скачет, или другими словами, подача температуры и peratu стадо стены для особых случаев. Для заданного температурного поля, Т、 ч = я 1. Прямые, но несколько громоздкие вычисления показывают, что в этом случае все константы c равны 1. Затем, используя ранее описанный способ, рассчитывают теплопередачу к пластине, в которой температура стенки изменяется произвольно. Точка$ ₂ в каждом значении температуры d / s, d / da₂,. ., Д /да₃ .. Если он изменяется один за другим (рис. 7-6), то поток Тепло от стены на длине x подчиняется последнему уравнению 7 = £А (х, уй ^. (7-17) Я. .Рис .7-6 .
Постепенное изменение температуры стенок、 В этом уравнении a представляет собой коэффициент теплопередачи .Это представляет собой тепловой поток вдоль длины x, если есть только 1 шаг D / w .— в точке GI температура стенки .Этот коэффициент теплопередачи в условиях ламинарного течения задается формулой (7-13) (при условии, что передняя часть пластины не нагревается до Х=£, если заменить Хо на рис .7-6), в противном случае необходимо добавить дополнительный температурный шаг — (для c, = 0、 Где tₛ-температура жидкости вне пограничного слоя .— Непрерывно меняющаяся температура стенки может быть представлена в виде последовательности бесконечных скачков температуры dtw, таких как: Интервал де .
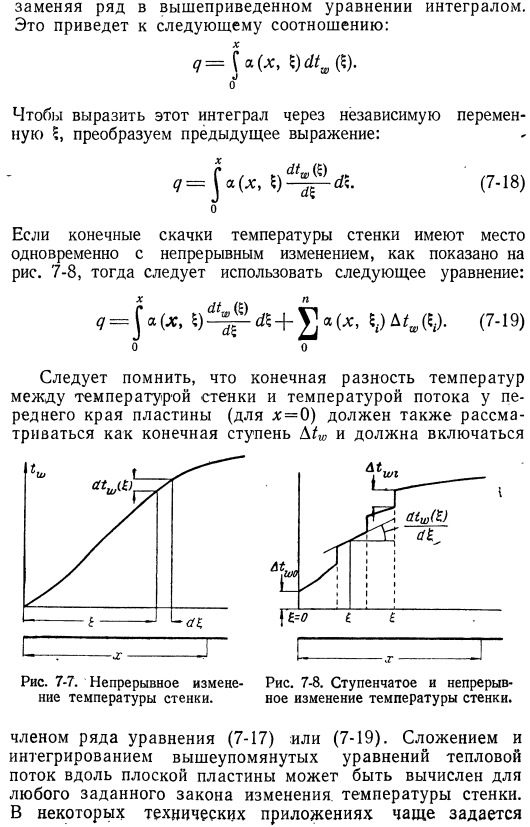
- Исходя из этого, можно получить значения теплового потока по длине x при изменении температуры стенки, как показано на рис .7-7 .Я поставлю его так близко, как только смогу .Замените ряд приведенного выше уравнения на Интеграл .Это приведет к следующим отношениям: ?= $ » (* .Да .Чтобы выразить этот Интеграл с независимой переменной 5, преобразуем предыдущее уравнение .?= йа (х, (7-18) Да .Если окончательный скачок температуры стенки происходит одновременно с непрерывным изменением, как показано на рисунке 7-8, то следует использовать следующую формулу: ₉ = Ja (X, +₍ ₍) ^ ^ (у .(7-19) О, да .
Обратите внимание, что конечная разность температур между температурой стенки и температурой потока на переднем конце пластины (для x = 0) также должна учитываться и включаться в качестве конечной фазы & tw .7-7 .Непрерывное изменение температуры стенки .Рисунок 7-8 .Постепенное и непрерывное изменение температуры стенки .Набор уравнений (7-17) или (7-19) members .By суммируя и интегрируя вышеприведенное уравнение, тепловой поток вдоль пластины можно рассчитать по любому закону изменения температуры стенки .Некоторые технические приложения часто спрашивают Тепловой поток на поверхности пластины превышает температуру стенки .
Пусть в системе, состоящей из двух тел {\displaystyle X}X и {\displaystyle Y}Y, тело {\displaystyle Y}Y (пробное) заключено в жёсткую адиабатическую оболочку. Людмила Фирмаль
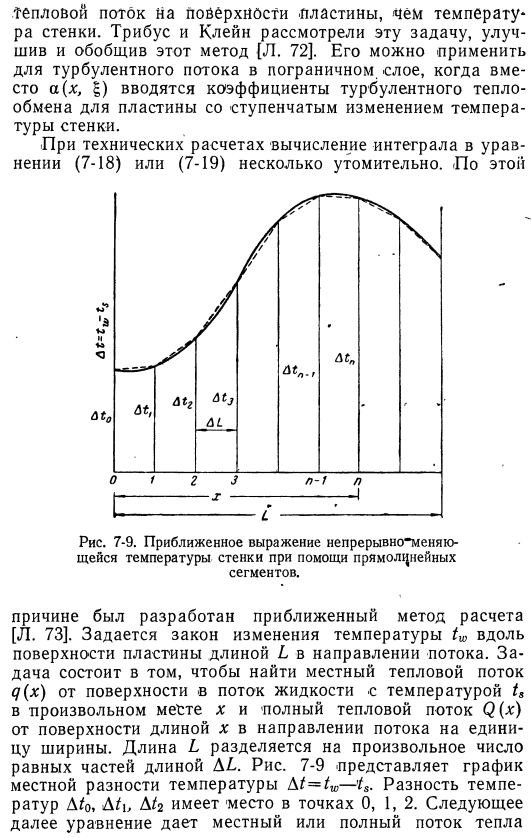
Трибус и Клейн рассмотрели эту проблему и улучшили и обобщили метод[L .72] .Когда вместо (x, §) в пластину, температура стенки которой изменяется ступенчато, вводится турбулентный коэффициент теплопередачи, его можно использовать для турбулентности в пограничном слое .В техническом расчете немного громоздко вычислить интеграл по формуле (7-18 (7-18) или (19-19) .С этим .Рисунок 7-9 .An приблизительное выражение температуры стенки, которая непрерывно изменяется с использованием отрезка прямой линии .Поэтому был разработан приближенный метод расчета[L .[73] .Указан закон флуктуации температуры tw вдоль поверхности пластины длиной L в направлении течения .
Задача найти местного теплового потока q (x) для потока жидкости при температуре tₛ произвольного пространства X от поверхности и общего теплового потока q (x) от поверхности длина х направление потока на единицу ширины .Длина L делится на равные части любого числа длины AL .7-9 ″ показывает график локальной разности температур t = tw —’tₛ .Перепад температур A/ o, A / b A / g возникает в точках 0, 1 .2 .Следующее уравнение дает локальный или полный тепловой поток Кроме того, в случае ламинарного или турбулентного течения, соответствующие физические константы берутся из таблицы .7-1 .: 7 (x) или* y — =a ₍ ₎ (l:) {d / ₍ ₍ ₎4-A (D ?In-A/₀) — f-6-XX | (2l-1) M-M, −2 (D /, 4-D /, + M, + .. + d i_.) ]), (7-20) a (x) .
Лкальный или средний коэффициент теплопередачи пластины с постоянной температурой стенки[уравнение(7-10)、(7-15)、(8-18)、(8-48)]。Формула (7-20) определяет тепловой поток в любой точке x на surface. It находится по адресу (1, 2, 3. .Соответствует любому из следующих (или любому из них) : n — количество позиций, совпадающих с точкой l* .Таблица 7-1 Локальный поток суммарного теплового потока Жара .А Б А Б Ламинарный поток .. .. .. 0. 995 0. 446 0. 969 — 0. 432 Турбулентность. .. .. 0. 991 0. 117 0. 982 — 0. 478 Уравнение (7-20) вводится путем замены действительной разницы между температурой стенки и температурой потока ломаной линией, показанной на рисунке. 7-9. Интеграл уравнения (7-18) решается для случая линейного изменения температуры стенки, и результат аппроксимируется уравнением 2-го порядка.
На основании этих данных можно найти значение теплового потока, соответствующее пунктирной линии. Для турбулентности (течения при интегрировании уравнения (7-18) мы использовали уравнение, показанное на стр. 273, которое объясняет критерий Нуссельта для постепенного изменения температуры. В сравнении с точным решением мы обнаружили, что погрешность в Формуле (7-20) составляет всего несколько процентов. Уравнение qc (x) = y0 (x) / d / n имеет вид nostyo является постоянной и равна Д / С. Поскольку постоянная а в Формуле (7-20) почти в 1, разница между местного теплового потока q (x) и qcx зависит от значения константы b.
Из табл. 7-1, видно, что разница между q и qc значительно больше, чем в ламинарный поток в турбулентный поток. Иными словами, история температуры течения в рассматриваемой сфере влияет на ламинарный поток значительно больше, чем в турбулентном потоке. Это также относится к потокам, которые проходят через трубы и channels. In случай турбулентности, доисторического периода следует рассматривать только тогда, когда температура в верхнем течении точки n меняется очень быстро.
Смотрите также:
| Уравнение энергии ламинарного пограничного слоя | Поперечное омывание цилиндрических тел |
| Движение жидкости вдоль плиты | Точные решения уравнения энергии ламинарного пограничного слоя |

