Оглавление:








Движение жидкости вдоль плиты
- Предположим, что для расчета температуры tw необходимо рассчитать теплопередачу от некоторой плоской пластины к жидкости с постоянной скоростью. Первая часть пластины имеет длину x₀, не нагреваясьне такую же температуру, как моющая жидкость (рис. 7-3). Гидродинамический пограничный слой начинается спереди Конец пластины и термический слой на границе нагревательной части пластины. Толщина как пограничного слоя 6, так и слоя 6 увеличивается в направлении течения.
Расчет толщины теплового пограничного слоя и с его помощью Рисунок 7-3. Гидродинамический пограничный слой и термический пограничный слой на плоской пластине. Теплопередачу можно осуществлять по формуле (7-2). Для этого необходимо сделать исходное предположение относительно формулы кривой распределения температуры пограничного слоя. Чем ближе принятый профиль к реальному, тем лучше будет результат исследования.
Без использования пробного тела первое начало теряет смысл содержательного закона и превращается в бесполезное для расчётов определение количества теплоты. Людмила Фирмаль
Для этой цели мы используем выражение, содержащее любую функцию, определенную таким образом, чтобы принятый профиль удовлетворял условиям, допустимым для фактического профиля. Если y = 0, t = tw. Для y = ^ t = t₅, g — = 0. Для y = n формула (7-5), записанная для медленного стационарного течения, имеет вид: Согласно этим 4 требованиям. Вам нужно использовать полином со следующими 4 функциями: Т-ₐ — — с- — cy2- — ды Кроме того, если введена разность температур 0 = / / — tw, а функция определяется из приведенных выше условий, то кривая распределения температуры представляется следующим уравнением: __1 —_2__£___ l / jlv 2. 2.
Здесь 0 = -/»; 6、= /、- Теперь вы можете вычислить Интеграл уравнения теплового потока Мне. Предположим, что тепловой пограничный слой меньше, чем гидродинамика. Тогда для z />8ₚ0 =oₛ 2-й Интеграл требует верхней границы y = bp, потому что подынтегральное выражение исчезает. Предполагая, что c = 8z / 8, вычисляя Интеграл, мы получаем: Предполагается, что 8 8, следовательно, c 1, поэтому 2-й член в правой части уравнения очень мал по сравнению с первым членом и может быть проигнорирован. Рисунок 7-3 показывает, что коэффициент c является функцией x. Если подставить последнее интегральное значение в Формулу (7-2), то оно становится: Или с. 20. Подставляя значение bdbjdx для.
Формулы (6-27) и значение s2 для Формулы (6-28), получаем: отношение v / a представляет собой безразмерную величину, обычно встречающуюся в расчетах теплопередачи, называемую критерием Прандтля, как указано выше, и обозначается символом pr. ПР = 1=¥ — (? -⁶) Поскольку значения критерия Прандтля определяются физическими параметрами, сам критерий является параметром. Его преимуществом является безразмерность. В таблице приложения приведены значения критериев Прандтля для жидкости и газа. Значения теста Прандтля жидкости и газа зависят от температуры. Выраженная зависимость давления наблюдается только вблизи критической точки.
Изменение величины эталонного pr по температуре газа незначительно. Если мы введем численный pr в уравнение выше, это выглядит так: ГЗ и 4 Д&) _ 13 x 3 x dx » 14 rg» Или заменить v = y, 4 ды 13 3 х dx ~ ~ 14 РГ• Частичное интегрирование равно/ / = 13 / (14 pr). Общее решение однородного уравнения можно найти по формуле y = x. Где n-пара /₄. So, полное решение вышеприведенного уравнения принимает вид: И-13-4-gg-3/ 14 РГ. Из граничных условий x =x, c = 0 или= 0: Если пластина разрезана по всей длине (x = 0)、 1, 026 ^ РГ (7-8) Вязкое масло имеет стандарт prandtl pr = pooo или больше. Для этих жидкостей толщина теплового пограничного слоя составляет лишь 1/10 толщины гидродинамического пограничного слоя.
Критерий Прандтля для газа меньше, чем 1. In в этом случае£больше, чем* 1, поэтому предположение, сделанное в приведенном выше расчете, здесь недействительно. Однако минимальное значение газа составляет pr = 0, 6, поэтому£= 1, 16, и погрешность из-за вышеуказанного предположения очень мала. Единственным веществом, характеризующимся очень малым значением критерия Прандтля, является жидкий или расплавленный металл. Для них результат, полученный по формуле (7-8), не подходит. * Тепловой поток от печи на единицу площади определяется по формуле С другой стороны, тепловой поток также может быть определен с использованием коэффициента теплопередачи А.
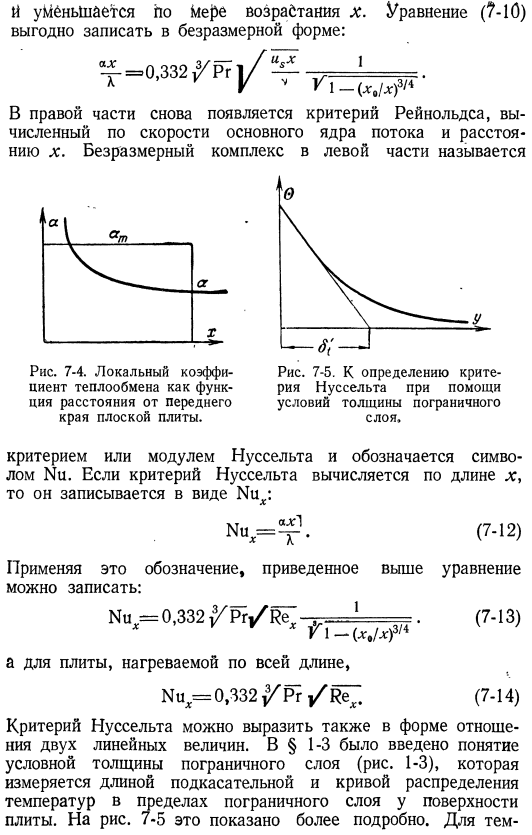
Приравнивая правую часть этих уравнений, получаем: Поэтому коэффициент теплопередачи обратно пропорционален толщине теплового пограничного слоя. Подставляя значение c в Формулу (6-28), получаем: а = 0, 3322 ^ ПР] / » с (7 дней) А если печка нагревается по всей своей длине、 а = 0, 3322 (7-Р) Как видно из графика на рисунке* 7-4, коэффициент теплопередачи бесконечно велик в начальной точке нагревательного участка d уменьшается по мере увеличения x. Уравнение (7-10) выгодно описывать в безразмерном виде. 1. ______ u1- (x / x) 3′ ⁴ ’ Критерий Рейнольдса снова отображается с правой стороны и рассчитывается по скорости и расстоянию x основного ядра потока.
- Безразмерный комплекс слева называется Рисунок 7-4. Локальный коэффициент теплопередачи в зависимости от расстояния от передней кромки пластины. Рисунок 7-5. To определите критерий нуссельта, используя условие толщины пограничного слоя. Критерий нуссельта или module. It обозначается знаком nu. Когда критерий Нуссельта вычисляется по длине x, он описывается в виде Нуₓ. Нуₓ= ^ — (7-12) Вы можете использовать эту нотацию, чтобы написать уравнение выше. 1ч = 0. 332 ург / е; (7-13) А если печка нагревается по всей своей длине、 nuₓ= 0. 332 / Ор / РТ. (7-14) Критерий нуссельта также может быть выражен в виде отношения 2 линейных величин.
В § 1-3 введено понятие условной толщины пограничного слоя (рис. 1-3). Это измеряется длиной касательной и кривой распределения температуры в пограничном слое поверхности пластины. ФЛА рис. / — 5 показано более подробно. Для В случае температурной кривой формы 3-й параболы установлена зависимость 8Г= 2 /38Г. От 1 до 3, коэффициент передачи тепла Таким образом, стандарт нуссельта Равно отношению длины x к условной толщине теплового пограничного слоя 8’. Толщина пограничного слоя всегда меньше длины x, поэтому значение критерия Нуссельта больше.
По изменению внутренней энергии пробного тела можно будет судить о количестве теплоты, переданном от системы пробному телу. Людмила Фирмаль
Толщина теплового пограничного слоя уменьшается с увеличением опорных значений Рейнольдса и Прандтля. Поэтому оба эти значения увеличивают значение критерия нуссельта. При расчете промышленных теплообменников важно знать среднее значение коэффициента теплоотдачи, а не локальное. Для пластины, нагретой по всей длине, среднее значение коэффициента теплопередачи (М5> О * Где константа c содержит это значение и является x независимым. Из соотношения (7-15) видно, что среднее значение коэффициента теплопередачи равно в 2 раза значению локального коэффициента теплопередачи на краю пластины.
Теплопередача от печи, нагретой по всей длине, также рассчитывалась путем точного решения дифференциальных уравнений пограничных слоев. Эти вычисления дают выражение с числовым коэффициентом 0. 332 (7-14). Такое близкое совпадение приближенного решения и результата является, конечно, случайным. Если физические параметры уравнения зависят от температуры, то их значения должны быть получены при средней температуре. Из расчетов при решении уравнений ламинарного пограничного слоя жидкости, характеристики которой изменяются, показано, что для физических параметров формула (7-14) дает правильное решение задачи о воздухе.
Тра получают при определенной температуре, определяемой из соотношения. _tt = = 0. 50 [l. 69]. (7-16) Эта определенная температура может быть применена к другим газам. Для жидкостей знание определения температуры не ясно. Эксперимент подтвердил справедливость уравнения для газов (7-14). Формула (7-13) — (7-15) получена в предположении, что отношение толщины теплового пограничного слоя к толщине гидродинамического пограничного слоя меньше 1. It было установлено, что это относится к потокам, где число прандлей больше 1. Этот раздел расчета полностью приемлем, если отношение£больше 1.
Однако если скорость равна 0 y 6 и u = u) для (b y 6t), то она задается формулой (6-26), поэтому Интеграл должен выполняться через 2 интервала. Следующая формула справедлива для пластин, нагретых до определенной температуры по всей длине. Ню. = ——— = ___ Пр. ————- х 1, 55 / пр+ 3. 09 / 0. 372-0. 15 пр. * Это соотношение используется для расчета теплопередачи жидкого металла с числом Рейнольдса 0. 005-0. 05. In в этом диапазоне знаменатель практически не зависит от pr, поэтому критерий Нуссельта в основном зависит от произведения re pr, которое является критерием пекле.
Точное решение уравнения ламинарного пограничного слоя приводит к соотношению со слабой функцией pr, которая изменяется примерно от±5% ’до примерно 1, 98 для диапазона числа Прандтля выше, вместо знаменателя вышеуказанного уравнения[l. ]. _ 70]. Вот хорошее совпадение приведенной формулы с этим результатом: Пример. Рассчитайте коэффициент теплопередачи пластины в воздушном потоке на расстоянии 100 мм от передней кромки пластины. Печь нагревается по всей ее длине, скорость движения воздуха uₛ составляет 10 м [с, температура воздуха^ = 52°С, температура поверхности печи/ á á = 124°С.
Коэффициент кинематической вязкости воздуха при 100°С и атмосферном давлении составляет от 2, 36 до 10″⁸m * {s (см. Приложение). Следовательно, критерии Рейнольдса reₓ= 46 600. Из приложения найдите критерий прандля pr = 0, 695. Критерий нуссельта определяется по формуле (7-14) : nuₓ= 0. 332- / 0. 695 ′/ 46 600 = 63. 3。Из Формулы (7-12) Коэффициент теплопередачи на расстоянии 100 мм от передней кромки пластины: a = (x / x) 63, 3. Теплопроводность воздуха 0. 0276 100°cx = 0. 0276 ккал / м-ч-град следовательно, ⁼ ⁼_ _ j — * 63. 3 = = 17. 5 ккал] мг’ч-град.
Среднее значение коэффициента теплопередачи на расстоянии 100 мм составляет 33 ккал [мг’ч’град. Количество тепла, отводимого от плиты, которая имеет ширину 0, 31 м и длину 100 мм, выглядит следующим образом: q = 7 bx (^- q= 33•0. 31•0. 1(124-52)= 73. 5 ккал /ч.
Смотрите также:

