Оглавление:




Уравнение теплового потока через пограничный слой
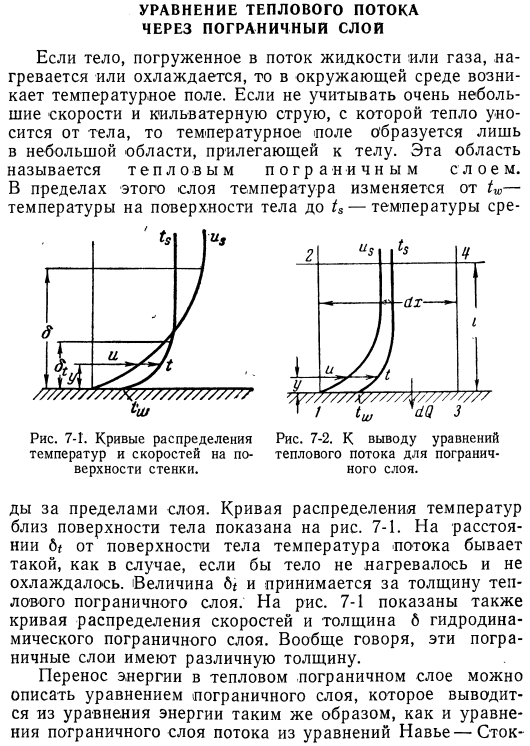
- Когда объект, погруженный в поток жидкости или газа, нагревается или охлаждается, в окружающей среде образуется температурное поле. Если не принимать во внимание очень малую скорость и след, в котором тепло уносится от тела, то температурное поле образуется только на небольшой площади, прилегающей к телу. Эта область называется термическим пограничным слоем. В пределах этого слоя температура изменяется от температуры поверхности tw-тела до tₛ-температуры Рисунок 7-кривая распределения температуры и скорости стенки L. Рисунок 7-2.
To вывод уравнения теплового потока пограничного слоя. Ды на внешней стороне слоя. Кривая распределения температуры вблизи поверхности тела показана на рисунке. 7-1.At на расстоянии b /от поверхности объекта температура потока может быть такой же, как и в случае, когда объект не нагревается и не охлаждается. величиной dₜ принято считать толщину теплового пограничного слоя. На рис. 7-1 также показана кривая распределения скоростей и толщина гидродинамического пограничного слоя, 6.In в общем, толщина этих пограничных слоев разная.
В Российской Федерации калория допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «промышленность». Людмила Фирмаль
Перенос энергии в термическом пограничном слое может быть описан уравнением пограничного слоя, полученным из уравнения энергии таким же образом, как уравнение пограничного слоя потока из уравнения Навье-стока. Уравнение теплового потока через тепловой пограничный слой может быть использовано для приближенного, но более быстрого и простого определения теплового пограничного слоя и тепла transfer. It предполагается, что плоскости 1-2 и 3-4 (рис.7-2-2), которые расположены на расстоянии dx друг от друга, от плоскостей 2-4 /параллельны поверхности тела, а стенки 1-3 и/больше толщины обоих пограничных слоев b и b/. в расчетах постоянные и скоростные свойства жидкости могут быть очень малы и ограничены 2-мерными задачами, так что повышение температуры за счет внутреннего трения пограничного слоя можно игнорировать.
Элемент объема показан на рисунке. 7-2 ограничивается плоскостями, параллельными плоскости чертежа и находящимися на расстоянии 1 от каждой other. In единицы времени, количество тепла, определяемое следующим интегралом, поступает из плоскости 1-2. 1. Рар г туды、 Да. Где с-удельная теплоемкость при постоянном давлении на единицу mass. At расстояние dx, это количество тепла составляет Таким образом, количество тепла, исходящего от объемного элемента через плоскость 3-4, больше, чем количество тепла, исходящего от этой величины, но только через плоскость 1-2 plane. As как показано в предыдущей главе, через плоскость 2-4 масса переходит в рассматриваемый элемент Жидкость, измеренная в P ^ x-jj I UD.
Вместе с этим 6. Тепло поступает в выбранный элемент с массой На стр. 1214 объясняется, почему необходимо брать удельную теплоту при постоянном давлении. определяется ПК ^ ДХ — £^udy. To определить Да. Определенное количество тепла возникает на поверхности объекта от параллелепипеда или в обратном направлении через плоскость 1-3.Поскольку частицы жидкости, расположенные на самой поверхности объекта, имеют нулевую скорость, это тепло должно передаваться на поверхность через этот слой жидкости посредством теплопроводности. Таким образом, формула (2-2) holds. In обозначения, принятые здесь, тепловой поток в единицу времени Где L — теплопроводность жидкости или газа.
- Для стационарного режима алгебраическая сумма количества тепла, поступающего в коробку из-за движения частиц, и количества тепла, которое удаляется из коробки на поверхность тела из-за теплопроводности, должна быть равна нулю. Мне. ?СР£с J * — 9Cₚ^^ tudy_X 0 ′ 0 Введя в это уравнение коэффициент теплопроводности. Мы получаем ’-2> О ( £ ) = ⁰ ⁰ — ⁽ > — ’ > Это уравнение теплового потока через пограничный слой, которое может быть использовано для расчета теплопередачи[L. 68]*.Физические параметры, включенные в Формулу (7-2), перечислены в таблице(см. Приложение).Значения удельной теплоемкости cp, коэффициента теплопроводности l и вязкости q зависят от давления только вокруг критического point. In в случае водяного пара эта зависимость показана на рисунке.
С-3 и P-7.In теория, удельная теплоемкость cp вблизи критической точки приближается к бесконечности. Это видно по очень крутому подъему кривой. * Курзирин впервые применил уравнение (7-2) для расчетов теплопередачи. СР вблизи критической точки(рисунок P-3).Плотность магнитного потока p практически не зависит от давления. Для газообразных он может быть вычислен из уравнения состояния. Вблизи критической точки зависимость от давления составляет complicated. As на примере рисунка Р-1 эта зависимость показана для воды и пара. Значения температуропроводности а и кинематической вязкости v жидкости зависят в очень малой степени от давления, если они не принимают значения, близкие к критическому давлению.
Как единица измерения теплоты используется также калория. Людмила Фирмаль
Для газа, обе эти величины обратно пропорциональны давлению. Температурная зависимость удельной плотности тепла и теплопроводности также может наблюдаться на рисунках Р-1, р-3, р-6 и Р-7.Особенно это заметно вблизи критического состояния. Формула(7-2) выводится в предположении, что характеристики потока постоянны. Поэтому его можно использовать для процессов теплопередачи, где есть разница температур и фактическое изменение свойств невелико. Вы можете расширить эту область применения формулы (7-2), введя правильно выбранное среднее.
Смотрите также:
| Поперечное обтекание цилиндра | Уравнение энергии ламинарного пограничного слоя |
| Обтекание осесимметричных тел | Движение жидкости вдоль плиты |

