Оглавление:




Обтекание осесимметричных тел
- Осесимметричный круговой поток вокруг объекта, погруженного в среду, дает по существу ту же картину, что и круговой поток вокруг цилиндрического объекта. Например, засады, которые обтекают шар, отрываются сбоку, а сзади есть застойная зона, заполненная вихрями. Это разделение происходит при большом числе Рейнольдса, но при очень низком значении (менее 1) критерия Рейнольдса ламинарный поток замыкается за шаром. Лобовое сопротивление, связанное с этим типом течения, описывается законом Стокса.
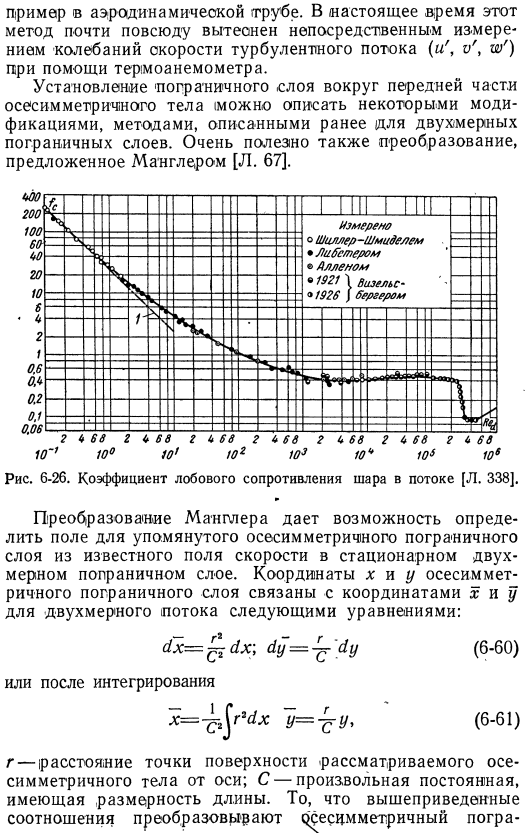
D = 3ttd i. Место происхождения: (6-59) Отображается коэффициент сопротивления шара в диапазоне больших значений критерия Рейнольдса. 6-26. Этот коэффициент определяется так же, как и коэффициент лобового сопротивления цилиндра. Опять же, характерное падение наблюдается примерно с 3-10 числами в Рейнольдсе number. It установлено, что величина критерия Рейнольдса, уменьшающего лобовое сопротивление в случае шара с гладкой поверхностью, зависит от турбулентности С.
Единица измерения в Международной системе единиц (СИ) — джоуль. Людмила Фирмаль
Это связано с тем, что степень турбулентности определяет, является ли пограничный слой перед точкой отрыва ламинарным или турбулентным. Эта зависимость между степенью турбулентности в свободном потоке и критическим числом Рейнольдса, на которое падает сопротивление шара, называется l. it был правильно истолкован прантором. Это позволяет использовать шарик для измерения турбулентности воздушного потока. Северный’ ^ Примеры аэродинамических труб.
В настоящее время этот метод был заменен прямым измерением флуктуаций скорости турбулентности (и’, v’, w’) с помощью термоанемометра, практически повсеместно. Установление пограничного слоя на фронте осесимметричного тела (некоторые модификации могут быть описаны выше для 2d пограничного слоя). Преобразование, предложенное Манглером, также очень полезно[l. 67]). Рис. 6-26. Коэффициент сопротивления шара в потоке[l. [338] Преобразование манплера позволяет определить поле указанного осесимметричного пограничного слоя из известного поля скоростей в стационарном двумерном пограничном слое.
Координаты x и y осесимметричного пограничного слоя связаны с координатами x и y двумерного потока следующими уравнениями: ДХ— ^ ДХ ды = — ^ ды Или после интеграции (6-61) g-расстояние от оси точки поверхности рассматриваемого осесимметричного тела. C-произвольная константа с размером длины. Дело в том, что приведенные выше соотношения преобразуют осесимметричную границу Разделение слоя на 2 измерения можно подтвердить, записав уравнения течения с осесимметричным пограничным слоем и введя в эти уравнения указанные выше преобразования.
Непрерывное уравнение для осесимметричного пограничного слоя (6-20) удовлетворяется введением функции потока y\ (dy¥1du = ri1c, dc ’/ dx = — ri / c). В этой формуле уравнение импульса (6-16) принимает вид: С ДФ д / с ДФ Д Д 1С г ду ДХ Р ду) г ДХ ду г d. g, a / c df> 1 1 dr дю Л К Р ^ Л-П ДХ Введение новой независимой переменной хны приводит к выражению гг СФ д / ДФ _g2sf д / ДФ СГ ДХ ду ду) s2dx ду ду / s2do Л Л у ду) s2r-это ДХ Поскольку обе части уравнения могут быть разделены на g2 / s2, уравнение идентично уравнению 2-мерного пограничного слоя (6-43), включая дополнительные члены, представляющие давление.
- Это означает, что двумерная функция потока пограничного слоя, представленная координатами x и y, является решением осесимметричного пограничного слоя в координатах x и y, если граничные условия одинаковы для обоих случаев. Для твердой»поверхности» сохраняется сходство граничных условий поверхности (w = 0). Сходство граничных условий на внешней кромке пограничного слоя требует, чтобы осесимметричный градиент давления потока (dr / dx) был идентичен 2d градиенту давления потока (dpjdx). Если вы знаете текущую функцию, вы можете легко найти скорость. Задачи 6-1.
Если кривая распределения скоростей приближается к прямой или параболе, то при обтекании плоской пластины следует рассчитать толщину и коэффициент трения ламинарного пограничного слоя. Сравните эти результаты с результатами, полученными в разделе 6-4、 6-2. Предполагая, что расход в этом диапазоне приблизительно задается следующим уравнением, необходимо рассчитать создание пограничного слоя вблизи передней шины кругового цилиндра с площадью поперечного сечения. Dujdx = 4uqxld (uq-скорость свободного течения, d-диаметр).
Количество теплоты не является функцией состояния, и количество теплоты, полученное системой в каком-либо процессе, зависит от способа, которым она была переведена из начального состояния в конечное. Людмила Фирмаль
Толщина пограничного слоя при x = 0 равна dd / cfx = o в этой точке (в противном случае толщина пограничного слоя, графически нарисованная как функция x в положительном и отрицательном x, может быть определена из условия, что x = 0 имеет пересечение). 6-3. Сравните форму кривой распределения скоростей, описанной в уравнении (6-40), с точным решением пограничного слоя, показанным на рисунке. 6-17 можно графически изобразить зависимость расстояния до эквивалентного отношения толщины пограничного слоя, нанесенного от стенки к горизонтальной оси (параметры x и p можно сравнить и выразить в виде функции импульса пограничного слоя соответственно).
6-4. Решите уравнение (6-45) и получите скорость u =в первом приближении. Сравните результат 3-й итерации x с решением, полученным Блазиусом (рис. 6-16). 6 до 5. It необходимо рассчитать кривую распределения скорости трения на стенке и коэффициент трения установившегося ламинарного потока через канал, образованный 2 параллельными пластинами. Введите гидравлический диаметр в формулу для коэффициента трения[обратите внимание, что константа в этой формуле отличается от константы в Формуле (6-49) ]. 6-6. Необходимо рассчитать кривую распределения скорости в области входа в канал, который состоит из 2 параллельных стенок.
Примите ту же форму, что и кривая распределения, как показано на рисунке. С 6 до 18. Используйте уравнения непрерывности и Бернулли для вычисления скорости и для вычисления интегрируемого уравнения импульса для центральной части и всего профиля скорости. 6-7. Однако вы должны повторить расчет, показанный в предыдущем вопросе, предполагая, что поток является турбулентным, начиная от входа в канал и используя закон 7-го порядка для кривой распределения скорости вблизи стенки. Сравните длину входа ламинарного и турбулентного потоков. 6-8. Объясните, почему коэффициент сопротивления конечного цилиндра меньше, чем у бесконечно длинного цилиндра.
Этот факт можно увидеть на рисунке. 6-25. Для этого рассмотрим распределение давления вокруг цилиндра, включая концевую область цилиндра конечной длины. 6-9. Если вам нужно определить степень турбулентности на скорости 30 и 180 м, рассчитайте размер шара! Во-вторых, обычные атмосферные условия. 6-10. Рассчитайте размер капель. Это означает, что если есть восходящий поток в воздухе со скоростью 0, 3, он может оставаться в воздухе в подвеске, не падая на землю. Л / С при нормальных атмосферных условиях.
Смотрите также:
| Движение жидкости в трубе | Уравнение теплового потока через пограничный слой |
| Поперечное обтекание цилиндра | Уравнение энергии ламинарного пограничного слоя |

