Оглавление:











Движение вдоль плоской стенки
- Используя формулу (6-8), рассчитайте толщину границы (слой поверхности плоской стенки с установившимся потоком). Рис. 6-10. Ламинарный пограничный слой на плоской пластине. Как уже упоминалось выше, » поверхность пластины вблизи передней кромки имеет слоистый пограничный слой (рис. 6-5). * Поскольку жидкость вне пограничного слоя постоянна по всей пластине, согласно уравнению Бернулли, давление также постоянно, так что последний член формулы (6-8) disappears. As результаты измерений показывают, что кривая распределения скоростей (sg) слоя на ламинарной границе имеет форму кривой, показанной на рис. 6-10.
Решение, предложенное t, pocket om, является、 Предполагая любое выражение распределения скорости по фиксированному числу ^ констант? Он рассчитывается при определенных условиях conditions. As для последнего условия присутствуют на поверхности стенки (i / = = 0) или на пограничном слое и границе течения (*/= b). Известно при r / = 0 (6-21) если y = b (6-22) Постоянное давление при y =, если уравнение пограничного слоя (6-16) описывает r / = 0 г =0. (6-23) Оставляя пограничный слой y> 8, кривая распределения скоростей должна отражать существование постоянной скорости uₛ без образования разрывов непрерывности.
Внутренние источники теплоты — понятие теории теплопередачи, которое описывает процесс производства (реже поглощения) тепловой энергии внутри материальных тел без какого-либо подвода или переноса тепловой энергии извне. Людмила Фирмаль
Так что если y = 8 г — =0. (6-24) Это является необходимым условием. Если y = 8, это показывает, что производные 2-го порядка, 3-го порядка или другие производные более высокого порядка также равны 0. Однако здесь меня устраивают 4 условия (6-21) — (6-24). Поэтому для профиля скорости можно выбрать выражение с 4 неопределенными коэффициентами. Например、 у = a + по +су24-dy3 (6-25) Эти коэффициенты можно определить, подставив формулу (6-21) — (6-24) в Формулу (6-25). Они выглядят так: Л Л 1、 а = 0; * = 2Д -; с = 0; д= ——- 2 «-^ Кривая распределения скорости определяется уравнением i-4-s-it) ’ (» ■«).
Используя эту формулу для интеграла импульса формулы (6-8), получим: [- Г Т-Г (+) «] Х Х [я-4 ++ 4 (Ф) ] ^ если y> 6, то верхний предел некоторых интегралов пришлось изменить на 6, так как скорость u =uₛ и подынтегральная функция исключаются, а формула (6-26) справедлива только для p <8. Умножьте выражение в скобках, а затем запустите интеграцию следующим образом 39 гр. 280₽ » л Градиент скорости вблизи поверхности пластины определяется из уравнения (6-26). _____ 3-、 /И > 2 d 3. 2 Д ’ Итак, напряжение трения на поверхности выглядит следующим образом: Подставляя значение/в это уравнение и уравнение импульса [уравнение (6-8) ], получаем следующее дифференциальное уравнение: 39₌ 280p 2.
Когда вы изолируете переменную, она выглядит так: (6-27) Если вы консолидируете последнее выражение, Вы получаете: 8 = 4, 64 1 / — константа (6-28) при x = 0 толщина 3 равна нулю, поэтому, если x измеряется от переднего конца пластины, константа интегрирования равна нулю. Формула (6-28) показывает, что 8 увеличивается пропорционально квадратному корню расстояния x. It удобно придать этому выражению безразмерный характер: 4. 64 Радикальным выражением является критерий Рейнольдса для расстояния x от передней кромки пластины. •Если это выражение обозначено reᵥ, то получается следующее уравнение: 4. 64 (6-29) Икс.
Таким образом, толщина пограничного слоя 6 измеряется им (расстояние от поверхности пластины, скорость определяется по формуле (6-26), достигает скорости основного ядра потока. Определение толщины пограничного слоя является несколько произвольным. При регулировке ламинарного пограничного слоя Эквивалентная толщина пограничного слоя. Это означает, что кривая распределения скоростей асимптотически приближается к значению основной скорости потока only. In при этом форма кривой распределения скоростей по толщине пограничного слоя по приведенному выше определению не имеет конечного значения. Применялись и другие определения.
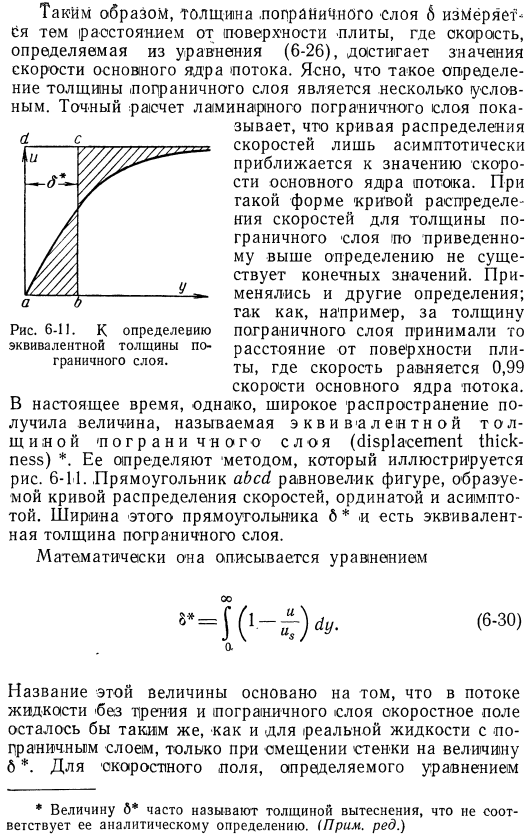
Например, толщина пограничного слоя принимала расстояние от поверхности пластины, поэтому скорость составляла 0, 99. Скорость основного потока ядра. Однако величина, называемая эквивалентной толщиной выравнивания (толщина смещения) *пограничного слоя, в настоящее время широко используется used. It определяется методом, показанным на рисунке». С 6 по 11. Прямоугольники равны фигурам, образованным кривой распределения скорости, ординатами и асимптотами. Ширина b * этого прямоугольника эквивалентна Толщина пограничного слоя. Математически она описывается уравнением (6-30).
Название этой величины основано на том, что в потоке жидкости без трения и пограничного слоя поле скоростей останется таким же, как и в реальной жидкости с пограничным слоем, только если стенка смещена на величину b*. Для поля скорости, определяемого уравнением значение * b * часто называют толщиной смещения и не соответствует определению анализа. (Примечание, редактировать) (6-26), приведенный выше Интеграл дает следующий результат: 8 * = 0, 3758 = Количество упражнений дается по формуле (6-12) 2 ₍=>₍=⁰- 13 ⁰ $ 7. Далее, напряжение трения возле стены 0, 323? М2. (6-31) Вместо этой величины часто используется коэффициент трения fₚ.
Это соответствует силе (сопротивление движению-величина, деленная на площадь поверхности пластины и площадь поверхности пластины и динамическое давление потока). Необходимо различать 2 величины. Локальный коэффициент трения fₚ и уравнение среднего коэффициента трения ■ cjx = Ф/, ДГП ^-、 Откуда? 2-й можно найти из равенства б ф * j-2. О Откуда? Икс. О, да. Ф 1. 292 Или Более точный расчет: для числителя этой формулы»на основе решения уравнения пограничного слоя получаем 1, 327, то есть значение 3%». Формула хорошо согласуется с экспериментальными результатами. Пример 6-1. It необходимо определить толщину пограничного слоя на расстоянии 100 мм от передней кромки пластины с учетом движения воздуха вдоль поверхности.
Скорость ветра 10 м {с, температура 16°С, давление-Атмосферное давление. Найдите критерии Рейнольдса. 10. 0, 1 ᵥ — / 48. Ю-с — ⁶⁷⁵⁰⁰ — Значение коэффициента кинематической вязкости берется из таблицы приложения. Соотношение толщины пограничного слоя и расстояния от передней кромки пластины И 4. 67 х / 67, 500 — ⁰ ⁰1⁷⁸ ’ Толщина пограничного слоя на расстоянии 100 мм от кромки составляет 1, 8 мм. Эквивалентная толщина пограничного слоя равна b * = 0, 6 мм. Это свидетельствует о том, что при нормальной скорости и расстоянии толщина пограничного слоя достигает примерно 2 мм.
Для турбулентного пограничного слоя определена кривая p a, а кривая скорости имеет гораздо большую кривизну, чем для ламинарной границы layer. An соответствующая аппроксимация фактического распределения скоростей задается уравнением Прандтля. (6-32) Однако, в области непосредственно на поверхности пластины, формула не правильная. Это можно подтвердить, рассчитав напряжение сдвига на поверхности. Градиент скорости Дю. 1. ⁷ ’ То есть она будет бесконечно большой на поверхности пластины (z / = 0). В результате напряжение сдвига на поверхности должно быть бесконечно большим, что физически impossible. In на самом деле, турбулентность всегда исчезает на поверхности.
Фактическое условие состоит в том, что между турбулентным пограничным слоем и поверхностью пластины существует ламинарный поток, скорость которого равна Рис. 6-12. Ламинарные и турбулентные пограничные слои. Он плавится прямо пропорционально изменению координаты y. Вне этого подслоя справедливо выражение (6-32). Расчетная кривая (распределение скоростей сопряжено на границе (подслое, образующем очень малый угол), как показано на рис. 6-12). Здесь напряжение трения на поверхности пластины должно определяться прямым измерением. Если значение критерия Рейнольдса не слишком велико, а поверхность гладкая, то формула Блазиуса дает хороший результат.
- Tст = 0. 0228 п ^ (^-) л /⁴. (6-33) Формула выведена на основе Лаборатория экспериментальных результатов по движению жидкостей и газов в трубе. Шульц-Грунов (l. 48) экспериментально доказал справедливость этого уравнения для движения вдоль плоской пластины до re = ’ 10Для. Для более высоких значений критерия Рейнольдса существует очень сложное уравнение, которое будет рассмотрено ниже. Подставляя значение формулы импульса (6-8), значение формулы (6-32) и формулу (6-32), получаем: / = Р j и (, , -) ) ды = Ри ^ Р) ’^1 — (^j в’ ’] ды = я? ⁸ у’ — О, да. Здесь формула (6-32) справедлива только для y <8, поэтому интегральный верхний предел также следует заменить на 6.
Если y> » 8 и u =uₛ, интегрируемое выражение отсутствует. Подставляя интегральное значение/и уравнение (6-33) в уравнение импульса, получаем дифференциальное уравнение Когда вы изолируете переменную, она выглядит так: После интеграции вы можете: 8 = 0, 376. Константа. (6-34) Некоторые трудности возникают при определении интегральной константы. Из рисунка 6-5 видно, что начальная точка турбулентного пограничного слоя находится на некотором критическом расстоянии xc от ведущего edge. At в этой точке ламинарный поток возникает из пограничного слоя и поэтому уже имеет определенную thickness. At в этот момент оба слоя будут соединены.
Тепловыделение при работе электрического тока. Людмила Фирмаль
Турбулентность и импульс ламинарного потока、 perreidownup. Рис. 6. 13. Ламинарные и турбулентные пограничные слои на плоской пластине. Здесь равные слои равны. Л. Прандтль. 49] (рис. 6-13), при определении толщины турбулентного пограничного слоя формула (6-34) хорошо согласуется с измеренными значениями. Начнем с передней кромки и предположим, что в этом месте толщина равна нулю. Недавние экспериментальные наблюдения показывают, что это не совсем верно, но мы принимаем это упрощенное предположение
. Константа в уравнении (6-34) равна 0, где x представляет собой расстояние от ведущего edge. In эталонная форма, выражение (6-34) принимает вид: б __ 0. 376 _ 0. 376 * (РЕ) 1 ’»• Критерий Рейнольдса, рассчитанный для расстояния x, снова появляется справа от уравнения. Эквивалентная толщина турбулентного пограничного слоя по формуле (6-32) равна 6 * = 3/8, а величина 8 = ^ 8. Если на критическом расстоянии вычисляются как ламинарные, так и турбулентные пограничные слои, то последние будут толще. Бегущий. Важно нельзя сразу увеличивать толщину пограничного слоя. • Происходит переход от ламинарных к турбулентным пограничным слоям.
Переходная зона 6-13 показана на фиг. Переход от ламинарного к турбулентному в пограничном слое начинается с относительно большой длины волны колебаний. В основном, эти колебания имеют ту же природу, как и волны, которые можно наблюдать при обтекании вертикальной пластины в пограничном слое в случае естественной конвекции (рис. 11-11). V. tollim-n [l. 50] и x. schlichting (l. 51), когда толщина пограничного слоя достигает определенного значения, движение пограничного слоя становится неустойчивым при колебаниях определенной длины волны.
Эти колебания всегда присутствуют в потоке за счет действия ряда раздражителей, отличных от внешних в неустойчивой области пограничного слоя, они не затухают, усиливаются в направлении течения жидкости, а волны постепенно приобретают неправильную форму и в конечном итоге полностью трансформируются в спирали. Эта зона очень трудна для изучения, и знания о процессе очень важны. Limited. To районы с установленной турбулентностью. При расчете последующей теплопередачи необходимо знать толщину q ламинарного потока подслоя. По этой причине необходимо быстрее определять скорость u на границе между турбулентным слоем и ламинарным подслоем.
В соответствии с напряжением трения на поверхности пластины происходит увеличение линейной скорости ламинарного течения подслоя. С ДУ Подставляя значение в это уравнение, получаем следующую формулу: решите это уравнение относительно y и имейте в виду, что если # = u = iib, это будет: 1 (в 0. 002281 b и b С другой стороны, если вы используете формулу (6-32), вы можете увидеть: Если мы сравним правую часть последних 2-х равенств, то получим выражение: 1, 878. (Образец:)/- (6-36) ) Здесь критерий Рейнольдса вычисляется по толщине пограничного слоя. Используя формулу (6-35), введем расстояние x.
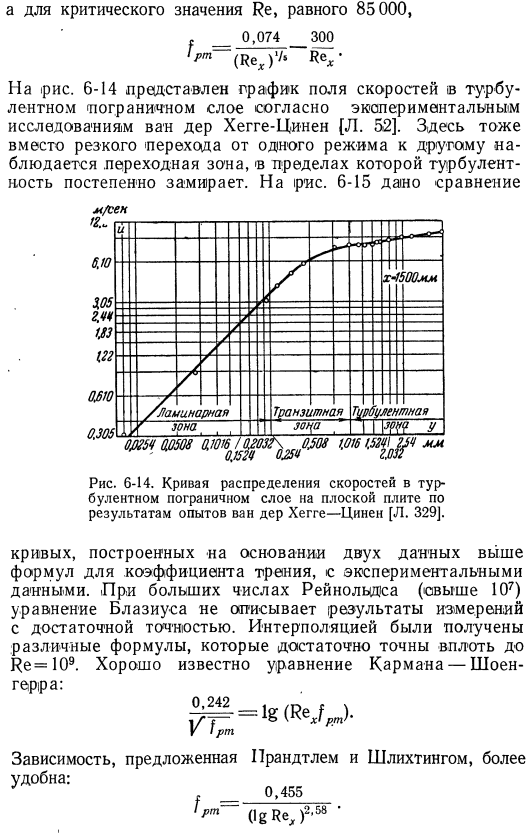
Я буду. 0. 1. (6-37) Толщина слоистого подслоя составляет、 Уравнения (6-38) Напряжение сдвига на поверхности пластины определяется из уравнения Или 0, 0296. (reₓ) °2 Сопротивление течению можно рассчитать по напряжению сдвига в области, где расположен ламинарный пограничный слой, и в области, где расположен турбулентный пограничный слой. Если критическое значение критерия Рейнольдса равно 485000, то этот расчет дает следующие результаты: f _°>⁷1 Если критическое значение re равно 85 000、 — °__3 На рис. 6-14 представлен график полей скоростей в турбулентном пограничном слое, экспериментально исследованный ван дер Хеггге-Зиненом[l. 52].
Здесь тоже вместо резкого перехода от одного режима к другому наблюдается переходная зона. Приведено сравнение рисунков 6-15 м / Сэн Рисунок 6-14. Экспериментальные результаты ван дер Хегге-Зинена показывают, что кривая распределения скорости турбулентного пограничного слоя на плоской пластине[l. 329j. Кривая создана на основе приведенной выше формулы коэффициента трения и 2 данных экспериментальных данных. Если число Рейнольдса велико (10 b и более), то уравнение Блазиуса не описывает результаты измерений с достаточной точностью. Интерполяция дала множество формул, которые были достаточно точными, чтобы re =10⁹. Уравнение кармана-Шена хорошо известно.
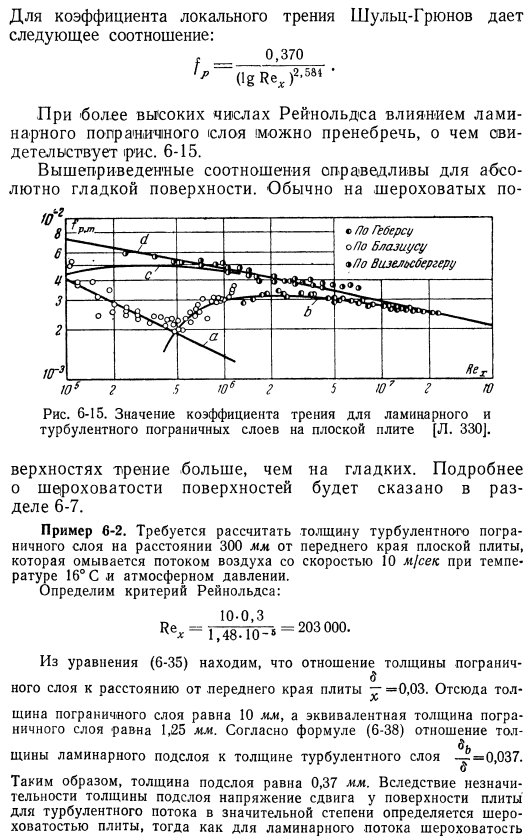
Камбуз:/ 77- » 1е (РЦ ^ м)」 Зависимости, предложенные Прандтлем и Шлихтингом, подробнее 0. 455. Rt ~~ (igrej2’⁵⁸’ Удобный. : ф Относительно локального коэффициента трения Шульц-гурнофф показывает следующее соотношение: 。 _____ 0. 370 ’⁷, _ (igrej2’⁵⁸» При более высоких числах Рейнольдса эффект ламинарного течения пренебрежимо мал. Это доказано в ip-Эс. 6-15. Приведенное выше соотношение справедливо для идеально гладкой поверхности. Обычно грубый Рисунок 6-15. Коэффициент трения ламинарного и турбулентного пограничных слоев на плоской пластине [l. [330]. По hebers о. Блазиус. е * по по wizelsberger ГХ. О * °б 1 — 7 —— 7 овощи Поверхность трения будет больше, чем гладкая.
Более подробно о шероховатости поверхности будет рассказано в разделе 6-7. Пример 6-2. It необходимо рассчитать толщину турбулентного пограничного слоя на расстоянии 300 мм от передней кромки пластины. Эта плоская пластина очищается потоком воздуха при температуре 10 м-сек. Температура 16°c, при атмосферном давлении. Определите критерии Рейнольдса. 10-0. 3-1. 48-10 — » −2⁰3⁰⁰°. Из уравнения (6-35) видно, что соотношение между толщиной пограничного слоя и расстоянием от передней кромки пластины равно= 0. 03. So, толщина пограничного слоя составляет 10 мм, а эквивалентная толщина пограничного слоя-1, 25 мм.
Согласно формуле (6-38), соотношение между толщиной ламинарного побочного слоя и толщиной турбулентного слоя составляет- = 0, 037. О Поэтому толщина подслоя составляет 0, 37 Лея. Поскольку толщина подслоя невелика, напряжение сдвига на поверхности пластины в случае турбулентности в значительной степени определяется шероховатостью пластины. Играют только второстепенные роли. Это можно объяснить тем, что если шероховатость не будет полностью покрыта слоистым подслоем, то напряжение сдвига и сила трения поверхности значительно возрастут.
Точные экспериментальные измерения показали, что сопротивление потоку резко возрастает, когда шероховатость примерно на 3-1 минуту превышает толщину слоя sublayer. In в этом примере поверхность пластины с шероховатостью менее 0, 1 мм можно считать гидравлически гладкой. Толщина побочного слоя ламинарного потока обратно пропорциональна скорости u и незначительно зависит от расстояния от переднего конца plate. At при высоких скоростях движения поверхность пластины следует обрабатывать с большой осторожностью, во избежание значительного увеличения ее сопротивления течению. Формула (6-33) справедлива только для гладких пластин.
Смотрите также:

