Оглавление:


Площади фигур, ограниченных плоскими кривыми
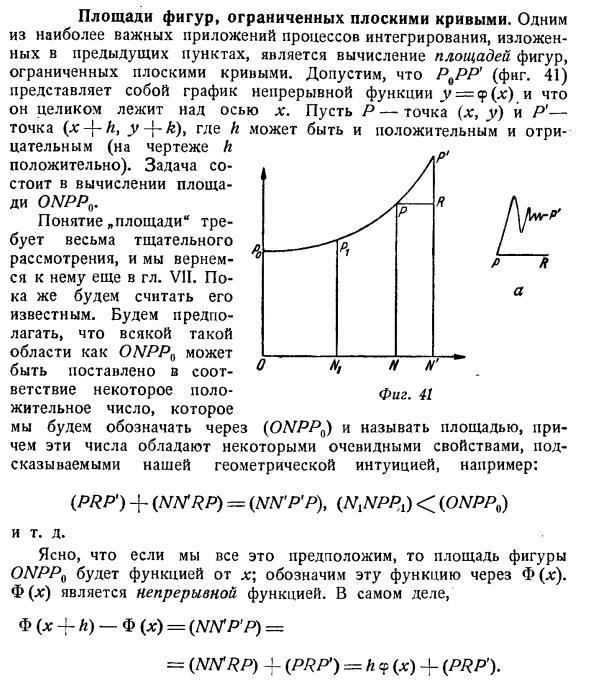
- Квадрат окружен плоской кривой. Одним из наиболее важных применений процесса интеграции, описанного в предыдущем абзаце, является вычисление площади фигуры, окруженной плоской кривой. P9PP ‘(fng.41) представляет собой график непрерывной функции y = y (x) и предполагает, что она полностью находится на оси x. Пусть P — точка (x, y), а P ‘- точка (x — \ — ht y + k) t. Где h является как положительным, так и отрицательным (h p на рисунке, положительный). Задача совместной работы состоит в том, чтобы рассчитать площадь OIRP0.
Предположим, что поле, такое как ONPPn, может быть связано с положительным числом. (ONPPn) указывает на эту область. Эти числа имеют некоторые очевидные характеристики, которые вдохновлены геометрической интуицией. Например: (PRP ‘) + (AJMRP) = (Ш’Р’Р), (N.NPP,) <(ONPP0) такие как Предполагая все это, ясно, что площадь фигуры ONPPq является функцией от x, эта функция обозначается через Φ (:) :). Φ (π) непрерывная функция. на самом деле фильтрат N ‘Рис. 41 Φ (χ + h) -Φ (:) 🙂 = (Р ‘Р)) = = (MVTRP) -f (PRP ‘) = h 9 (x) -f (PRP’)
Понятие «территория» необходимо очень тщательно рассмотреть и обсудить в главе 7, но предполагается, что оно известно в настоящее время. Людмила Фирмаль
| Алгебраические функции | Длины плоских кривых |
| Интегралы, связанные с коническими сечениями | Теоремы о среднем высших порядков |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Из чертежа видно, что площадь PRP меньше hk. Тем не менее, дуга PP не может монотонно увеличиваться или уменьшаться от P к PH, но это не всегда верно, потому что площадь PRP ‘всегда меньше, чем | A | X (/ g), где X (n) указывает максимальное расстояние любой точки дуги PP ‘от PR. С другой стороны, q (x) — непрерывная функция, поэтому она равна X 0 для η-0. Вот так Φ (* + Λ) -FI = / * {? (*) + K *)}.
Где | q (h) | 0. Следовательно, Φ (x) непрерывен. Кроме того, φ ‘(*) = 1nn + Hm {9 (g) + ^ (A)} = 9 (g). H-O P L-O Следовательно, ордината кривой * равна производной площади, а площадь является интегралом от ординаты. Теперь мы можем сформулировать следующие правила для нахождения области ONPP0: Вычислить интеграл от Φ (*) — 9 (x) и выбрать произвольную постоянную так, чтобы Φ (0) = 0. Затем Φ (x) является целевой областью. Если вам нужно вычислить площадь NxNPPlt, вам нужно определить произвольную константу и определить φ (π) =: 0 (x — абсцисса точки Px).
Если кривая находится ниже оси x, Φ (π «) отрицательна, а площадь равна абсолютному значению Φ (x). Людмила Фирмаль

