Оглавление:
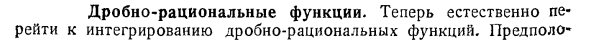



Дробно-рациональные функции
- Дробная рациональная функция. Теперь естественно перейти к интегрированию дробных рациональных функций. вероятно R (x) — дробная рациональная функция, выраженная в форме, рассмотренной в §118, то есть сумма многих Ряд слагаемых в виде слагаемых P (q 🙂 и ^ __ gyp. Вы можете быстро написать полиномиальные интегралы и интегралы для всех других членов, кроме одного с p = 1. на самом деле Независимо от того, является ли а реальным или сложным (см.
Параграф 118). Член с p = 1 довольно сложен. Непосредственно из теоремы (6) в разделе 114: (3) §F \ f (x)} f (x) dx = F {f (x)}. В частности, если взять f (x) для ax + b, a и b являются действительными числами, вместо F (x) пишется 9 (x), а вместо F ‘(x) пишется ^ (x 🙂 Итак, 9 (*) — это интеграл от φ (:) 🙂 J «φ (» * + *) dx = ± <f (ax + b). Например В частности, если а является действительным числом,Таким образом, вы можете видеть интеграл всех членов в R (x;), где p = 1 и a действительны. Есть еще термин, где p = 1, а a — комплексное число.
Чтобы найти интеграл от таких слагаемых, введем дополнительное предположение: предположение, что все коэффициенты действительны. Людмила Фирмаль
В этом случае a = y + B / — короткий маршрут Если уравнение Q (; e) = 0, комплексное сопряжение a = y-Ы также является корнем того же уравнения с той же кратностью. и Простейшая дробь ^ встречается в выражении R (x), тогда А ~ и дроби — тоже встречаются. Здесь A комплексно сопряжено с Ap. Это основано на природе алгебраических операций, с помощью которых можно найти и подробно изучить простые дроби в учебниках алгебры.
| Задача практического интегрирования | Алгебраические функции |
| Многочлены | Интегралы, связанные с коническими сечениями |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Так что, если термин происходит в развертывании Если R (x) входит в простую дробь, также встречается член x. Сумма этих двух слагаемых Эта фракция принадлежит следующему общему формату: Axe + B ax * — + 2bx + c ‘ Где b * ac. Читатель может легко быть уверен, что эти два типа эквивалентны. X, y, b представлены A, B, a, b следующим образом: , A D б? _ JF! K ~ Ta> — • 1-b- «G» » Где A = ac- и D-aB-M Предполагая, что F {f (x) \ равен 1n | f (x 🙂 | J ££ ld * = ln | / (*) |, (5) И предполагая, что f (x;) = (x; -X) 4 + v *, И по уравнению (6) в пункте 131 и (4) в этом пункте, J-281. ,, х-X + ** = AGS Эти два уравнения позволяют интегрировать сумму этих дробей в рассматриваемое разложение R (x;).
Таким образом, вы можете написать интеграл от рациональной функции вещественной дроби, который может разложить дробь на линейные множители. Интеграл такой функции состоит из суммы полиномов, определенного числа дробных рациональных функций вида A _1 _ п-1 (л: -а) п-1 * Если a — комплексное число, мы должны добавить, что указанная рациональная дробная функция, которая является частью интеграла, отображается с аналогичной функцией, где A и a заменяются комплексными сопряженными числами.
Две такие функции являются вещественными дробно-рациональными функциями Людмила Фирмаль

