Оглавление:








Движущиеся источники тепла
- Теплопередача в теле, возникающая при наличии движущегося источника тепла (или стока), имеет большое значение для технологии и широко применяется при упрочнении и охлаждении вращающихся систем С помощью дуговой сварки, поверхностного упрочнения, непрерывной разливки или струйного охлаждения теплоносителя. [l. [43] их анализ основан на представлении о том, что квазистационарное состояние получается, когда источник тепла расположен на достаточно большом объекте, а система находится в стационарном состоянии с точки зрения наблюдателя, движущегося вместе с источником тепла.
Для 3-мерной системы с декартовой системой координат уравнения могут быть применены, когда не учитывается источник тепла. ДТ / ДХ. ДЦ | ДТ-du2 ′ почтовый индекс dg2) ’ Предполагая, что свойства материала постоянны, количество тепла q ’ передается точечным источником света, движущимся вдоль оси с постоянной скоростью u. Предположим, что наблюдатель движется вместе с этим источником тепла и проходит через материал. Если вы дадите наблюдателю движущуюся систему координат, которая является его центром, эта система займет положение, показанное на рисунке. 5-2. Точки z * (x, y, z) неподвижной системы преобразуются в точки p (ξ, 7j, c) движущейся системы, поскольку при движении в направлении x другие координаты y = m) и z-t не изменяются, p (xy, z) = p (t, y). Вам нужно Рисунок 5-2.
Движущийся источник тепла был тщательно исследован Розенталем. Людмила Фирмаль
Система координат источника тепла для перемещения. Выполните преобразование переменной в стационарной системе координат (t = y, r, t). В новом ряду переменных b = x-h1, следовательно dcdx-1, dcdb =-и dx’1dc=. Поэтому преобразование приводит к выражению ДТ__ДТ д $ | ДТ ДТ ДТ ’ ДТ. Dt. D2t_ _ команда dh_, ¥л-d2l-dн _ _ _ _ _ d2l dx2-d ^2 ′ dy2-di? ’dz2~~ ~ d ^2 ’ Если эти замены производятся в Формуле (2-13), то получается формула (5-11). Выражение (5-11) принимает квазистационарный вид, так как величина d ^ db ’равна нулю с точки зрения исходного наблюдателя. ^ −4. -—— д $2 ′ dy2dz2 И dt_ д£ (5-12) Палочка. Рассмотрим стержень, аналогичный описанному в разделе 3-4, с постоянным поперечным сечением. Температура поперечного сечения считается постоянной.
То есть физически означает, что сопротивление теплопотерям с поверхности стержня намного больше, чем внутреннее сопротивление тепловому потоку самого стержня. Такое соотношение сопротивлений позволяет выравнивать температуру в каждой точке за счет высокой теплопроводности проводящего материала по сравнению с низким коэффициентом теплопередачи, регулирующим конвекцию losses. In в этом случае отсутствует температурный градиент dtjdy и dijdz. So, дифференциальное уравнение, соответствующее избыточной температуре, равно c) 2oqr g Тур — ^- = Лу^ — — — — -.
Термин конвекции Предполагается, что теплопотери с поверхности такие же, как§ 3-4, и приведенная выше формула принимает вид: Где m=} / ’ ac / xa. Введите переменную и выполните преобразование. Для квазистационарного состояния, как описано выше, из Формулы (5-13) И d2e24 / с n & = е — {ТТ! 2a* * f (ty, где f ($) должен быть defined. So, если мы дифференцируем выражение o и присваиваем его выражению (5-14), то имеем решение вида: Т (?) — [ (П^Г + ’. ]^) = ° — (5-15) В Формуле (5-15) имеется решение Ф ($) = ае «⁽+ быть〜» Куда? Ад. 」 И поскольку & =£⁽/2а* f (s), выражение для & принимает следующий вид: = = / 1 пп [+[|/ (г+ + КТ-я]! +) +«„₽(-[)/(£) ’+£+£] Я) * < Я6).
Соответствующие граничные условия, которые должны быть применены к формуле (5-16) являются: 0 = 0, £3±yoyo. Решение имеет 2 формы, согласно которым ’= l “ p[+ [] /(-£)’ +£r-yy] 1}£<⁰; ’ = »» p{-[/(£)’ +&+£]!} Если £ > ° — £ = 0, то температура обоих типов раствора равна и определяет максимум temperature. So, a = b = 0. Максимальный. <, -*. .»п {+[|/ (гг + н〜&]££ < ⁰ :=«^ «>> {-[/( с / + г+£]£) !> 0 .(5-17) Теплоту, текущую в каждом направлении от £-0, можно получить путем относительного дифференцирования и подстановки формулы из (5-17) .[/(£)» +> 4-£] k«, что дает следующее: [| /(^) ’+ 8 +] 1> 0-(5-18) Так как суммарная мощность источника тепла должна быть равна сумме положительных и отрицательных потоков.
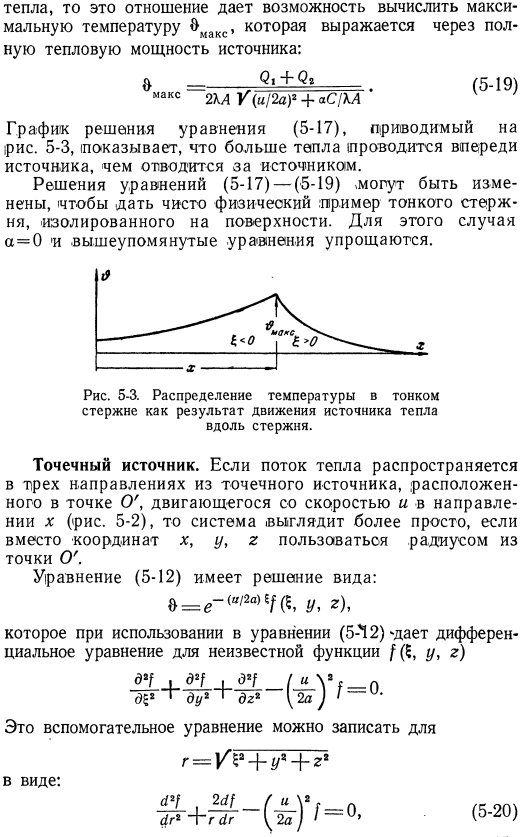
Тепло, то это соотношение позволяет рассчитать максимальную и максимальную температуру, представленную общей тепловой мощностью источника: & ________Ци 4-Qt_ _ _ _ Ф | Макс «2ХДУ (и / 2А) » + ас /ха ’ V’ График решения формулы (5-17) .5-3 доказывает, что перед источником проводится больше тепла, чем удаляется за ним .Необходимо исправить уравнение (5-17) — (5-19) >решение и привести чисто физический пример тонкого стержня, изолированного с помощью surface .In в этом случае a = 0 и приведенные выше уравнения упрощаются .Рисунок 5-3 .Распределение температуры тонкого стержня в результате движения источников тепла вдоль стержня .
- Точечный источник .При распространении теплового потока в 3 направлениях от точечного источника в точке O, движущейся в направлении скорости и x (рис .5-2), координаты x, y, z заменяют точку O’ .Решение в виде формулы (5-12) имеет вид: ⁽=⁽»⁽ дг / 2 ⁾ ⁾ 7 (^у、 Если использовать его в Формуле (5-42), то получим дифференциальное уравнение для неизвестной функции f (t, y, r du2’dz2 .Вспомогательным уравнением является Р = + + В следующем формате:, M_r_G / ₌ ₀dr * trdr 2a] 1⁴ (5-20) ) Поскольку начальная температура и температура поверхности являются изотермическими поверхностями концентрических сфер, то в этих квазистационарных условиях температура зависит только от R . Для этого требуется граничное условие O, удовлетворяющее понятию лучистого теплового потока от источника .
Эти граничные условия являются: О = 0; р — > сы; ДД _ д ’ д-р 4klg .* (5-21) Где q ’ — выход источника тепла .Решение формулы (5-20) равно g = fr [L .44]получим выражение Есть стандартное решение г =⁺ае{и /2А} GbE для〜{У, 2⁾Р⁾ Желательно получить решение & которое является формулой & = JL、 Подобный этому (5-22) Если применить граничное условие (5-21) и решить уравнение (5-22), то в итоге получим: Ох (г + 6) *»4lHg е (5-23) Решение (5-23) показывает распределение температуры вблизи источника движущейся точки в бесконечной среде .Этот результат почти верен для источников, которые движутся вдоль поверхности полубесконечной среды в количестве, где внешняя поверхность теряет тепло .
Поток жидкости течет равномерно в направлении x, а в плоскости X = b проходит через тонкую (тонкую) сетку, которая нагревается электричеством . Людмила Фирмаль
Это важно в сравнении с мощностью источника тепла .Использование этого анализа заключается в рассмотрении движения сварочного электрода вдоль поверхности очень толстой пластины с минимальными потерями .При решении сварочной задачи необходимо сказать: «как тепло (только этажом ниже!) » .Пластина принимается во внимание .Решение (5-23) » следует изменить так, чтобы его можно было описать .___ (г + г 2х е (5-24) Где q-тепло, выделяемое электродом .Вышеуказанные способы применяются в вопросах дуговой сварки, штамповки, упрочнения, отжига и прохождения снарядов по каналу пушки .Задачи 5-1 .Медная проволока пропускается через чертежную доску с постоянной скоростью .
Определите распределение температуры проволоки в зависимости от расстояния от чертежной доски, предполагая, что тепло, выделяемое трением, передается проволоке в плоскости, перпендикулярной оси чертежной доски .5-2 .Определите распределение температуры жидкости .5-3 .Лед образуется на поверхности озера от 0°С до −18°С .water .As слой льда утолщается, тепловое сопротивление уже образовавшегося слоя льда снижает скорость промерзания .
Вы получаете формулу, которая определяет толщину слоя льда как функцию time .As в первом приближении теплоемкость льда пренебрежимо мала .5-4 .При весе 1 361 кг он бежит со скоростью 48, 3 км в час, останавливается на 4 тормозах за 5 секунд, а площадь тормозной полосы составляет 258 .1cm2 .Каждая лента прижимается к стальному цилиндру с одинаковой площадью поверхности .Какое максимальное повышение температуры ожидается в этом случае ?Проанализируйте допущения, сделанные в решении .5-5 .
Если температура поверхности сферы поддерживается на уровне −15, 5°С, то рассмотрим замораживание объема сферы с начальной температурой 15, 5°С .плотность воды и льда одинакова (теплообмен наблюдается только в радиальном направлении .При этих предположениях уравнение теплопроводности сферы может быть преобразовано путем подстановки u ^ tr в уравнение теплопроводности полубесконечного тела для решения .Это так known .Do такое преобразование уравнения и получим решение сферы .Каковы допустимые значения уравнения ?
Когда это будет несправедливо ?Каковы другие методы физического анализа этой проблемы ?5-6 .It необходимо сварить 1, 83 м в длину, 0, 61 м в ширину, 2 стали толщиной 3, 2 м .Локальная температура сварочного электрода составляет 1647°C, а скорость-61 см {мин .Стальная пластина покрыта краской для предотвращения ржавчины .Рассчитайте площадь поверхности, которая будет окрашена снова после welding .Is конвекция с поверхности достаточно полезна ?
Смотрите также:
| Периодический перенос тепла | Различные виды теплообмена |
| Теплопроводность при плавлении или затвердевании | Пограничный слой и турбулентность |

