Оглавление:



Механические приложения
- Механическое применение. Естественно, что все геометрические и механические величины, связанные с распределением масс внутри объекта (V)в пространстве, являются, в принципе, простейшими для
использования принципа этого времени T R o y n y m и интеграла, а также суммы элементов бесконечно малых[ср. Н°204-20208 и 345]. Плотность распределения массы в любой точке Р-тела (V);
это функция координат точки; эту функцию мы всегда принимаем Людмила Фирмаль
непрерывной. Сумма элементов массы at=p Yu=p Ah AU (12) для размера массы целого [Г-жа № 375]. На основе базового статического момента, а^г=х у=ХС АУ, к ГХ=г=г? А Ху-хат-гр АС, (8) 338 [379]] Найдите самые статичные моменты: Тройной интеграл А на них-и координаты
центра тяжести: Шесть. Ч (ИЖ) 1Р не Да2 ‘ 17 g_(г_ _ _ _ т (19) Для D n p d n O G O тело R=SPST легко получается: х (ИЖ Девять. — ч Один» V9 К. (ЮУ В Координатные оси также понятны с первого взгляда. (И (П^ , 4=Щ(Х8+>2) Руй(в) Или относительно координатной плоскости: (11) 1У
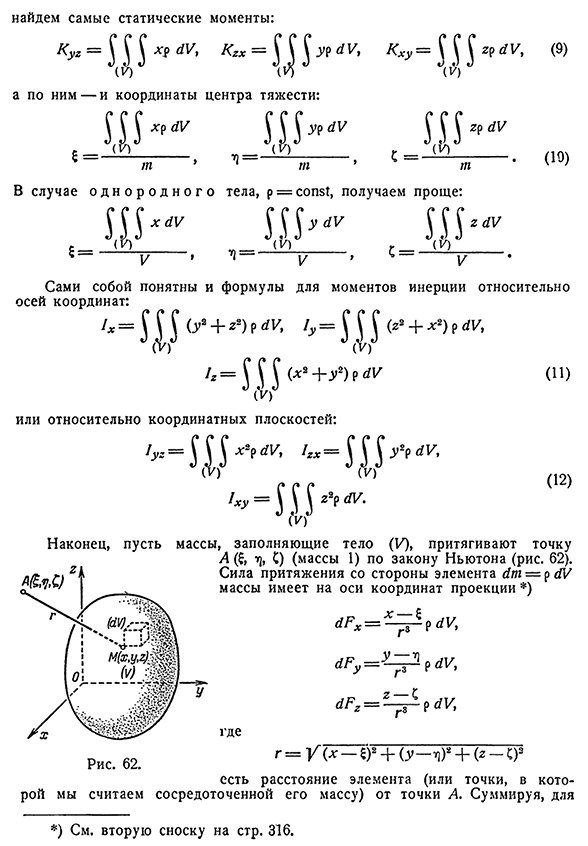
- г=я Р2Р АУ Г=Я тебя!(1А у’ 1х у=(22П и соч. г(V)) (12) Наконец, массы, заполняющие тело (V), притягивают точки A ( & ‘ * ], C) (масса 1) согласно закону Ньютона. 62). Притяжение со стороны элемента c1pg-R (масса 1u проецируется на оси) Arch=^=A? И u, Aru=u -^? в г, арг=г-=^4Г , См. Вторую сноску на стр. 316 (). Куда? Если вы суммируете
расстояние элемента (или точки, в которой, по вашему мнению, будет сосредоточена его масса) от точки А, то for380]§2. Формула Остроградского 339 Проекцию суммарной силы притяжения P на координатные оси получим х-е Г3 Точно так же определяется потенциал нашего тела в этой точке: (14) Если точка а находится вне тела, то все эти интегралы оказываются их собственными. В этом случае на основе соображений, аналогичных тем, которые используются в отношении простого интеграла [p°7]
дифференциального интеграла P7 по одной из переменных C & C, которая находится под знаком интеграла, так что мы получаем его. (B; Людмила Фирмаль
Y ‘ES’G'(15) если сама точка a принадлежит телу (V), то в этой точке g=0, и ее близкие (13) и (14) частичные статистические функции больше не ограничены. Однако эти интегралы существуют как «неуместные», и основные соотношения (15) соблюдаются. Для статического момента однородной цилиндрической балки (p=1) имеем следующее уравнение: ХХ г.х ху ых ю,у у у Г^А-ха-ю.\Р ) Они, конечно, следуют общей формуле (9). Например, г(х, г) К Х U=^у у U2yu=Ул Х У Л у г»г; Но 2 (- V. V) Около Отчет г=г(х, г) г=0 Это приведет к желаемому результату. В N°345 вместо вычисления последнего интеграла было включено рассмотрение из области механики (относительно статического момента базовой колонны).
Смотрите также:
Решение задач по математическому анализу
| Вычисление числа е на ЭВМ | Формула Лейбница для n-й производной произведения двух функций. |
| Локальные свойства непрерывных функций | Некоторые обобщения первого достаточного условия перегиба |

