Оглавление:




Вычисление тройного интеграла
- Вычисление тройного интеграла. И здесь мы переходим к вычислению интеграла N O V T o r n s X, который состоит из наименьшей кратности интегралов. Чем гарантируется наличие всех интегралов, присутствующих ниже, функция n o y в рассматриваемой области/(x, y, x), предполагая p e R s. Во-первых, тело,в котором
функция / (x, y, x)интегрирована, проецируется на плоскость x, где прямоугольник (T)=[a,b -, C,a -, e,/■] является прямоугольником (/?).) =[‘, ми.]/, Тогда, во-первых, b W/(x, y, x) y T=§y x§ / (x, y, x) (Г) Но (5) Заменив двойной Интеграл повторяющимся интегралом, можно в конечном итоге свести вычисление
тройного интеграла к последовательному вычислению простого интеграла: Б/Ш ф(х,г, х)г т=г г г-ых/г/(х,г, х) ых. Людмила Фирмаль
(D) А С Е наоборот, если первые два интеграла объединить в интегралы, то получим U сеть U сеть U’g^в (6) Двойной г, г) АГ,(7) Где: (f)=[a,6;C,y}. Во всех этих случаях, конечно, роли переменных x, y, x могут быть перестроены. Теперь предположим, что тройной интеграл берет на себя тело (V), отличное от прямоугольного параллелепипеда. Включите это тело между плоскостью x=x0 и плоскостью x-X и
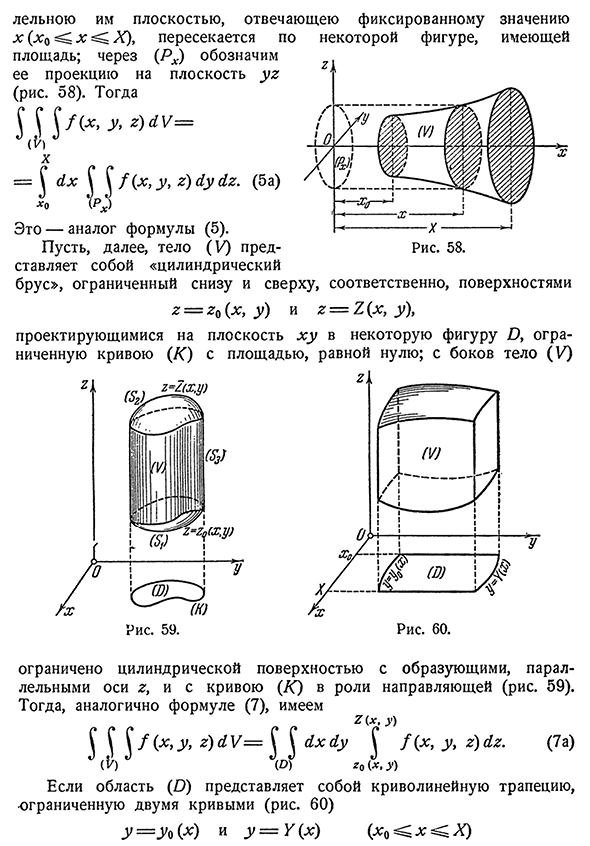
каждым Паралом-378]§1. Тройной интеграл и его вычисление 335 Плоскость, соответствующая фиксированному x (x0x X), пересекает область. 58). Тогда ((/(>у>г)г= Икс = \ <1x\ \ 7(x, y, x) c1us1x. (5A) XO Y является аналогом формулы (5). Пусть, далее, тело (V) ограничено ниже «цилиндрического стержня» и выше, 2=2H(x, y) и 2=X(X, y \ С некоторыми показателями Таким образом, поверхность На
- некоторых диаграммах плоскость проецируется на xy и заключена в кривую (K) с площадью, равной нулю, а тело в поперечном направлении(1/) Райс, 59. Она ограничена цилиндрической поверхностью с генератором, параллельным оси g, и имеет в качестве направляющей кривую (K) (рис. 59). Тогда, подобно формуле (7), мы имеем N? (х,Z>) г х г г Я/(х,г, х) г х. (7а) (Р)G0 и(ч>•) Площадь (если O• — трапеция кривой,ограниченная двумя кривыми (рис. 60) y=Y0 (x) и y=Y (x) (x0x X}336 глава XXIII. тройной интеграл[378 И
прямая линия x=x0, x=X, то тело (V) соответствует обоим вышеперечисленным типам. Замена двойного интеграла — будь то выражение (for) или выражение (7a), повторяется Это выражение обобщает выражение(6). Здесь, в самом простом случае, так оно и было. Рис 61. В приведенной выше формуле мы получаем N из переменных x, y, g. Это место и те перестановки Вверх-вниз-
P Lee MA 1) вычислить Интеграл (1X(12)) ПС(1++.Y+g) 8 ‘ x=0, y=0, 2=0 и распространяется на тетраэдр (K), ограниченный плоскостью Людмила Фирмаль
x+.Y+2=1 (рис. 61). Проекция тела на плоскость XY представляет собой треугольник, образованный прямой линией x=0, y=0 и x+y=1. Ясно, что граница изменения x равна 0 и 1, а в константе x этих границ переменная y изменяется от 0 до 1-X. Если и x, и y фиксированы、 По формуле (6А)、 1 1-х\ — х-у ‘Ч’ ч Максимыч(я++,+.>• 0-0. Зубец Мы последовательно вычисляем Интеграл, начиная с внутренней стороны: YG_1G1(1+x+ ^ + 2)3 _ 2 1(1 + * + ;u) 2 Н А К О Н ЕЦ 2И [(1+х+г) 2 Отчет 1379]§1. Тройной интеграл и его вычисление 337 2) вычислить Интеграл Дирихле предполагая p<7, g^1 (черт. 61). Используя формулу в виде (5A), поставьте интеграл от 2 вместо интеграла от x、: Один.
Заменив переменную, x=(1-2)^,, y=(1-уже известная[n°344,3)] Так что это Г (р)иди у) Г(Р+? +1) Наконец, используя известное выражение функции B[N°311, (12)], G (P)G (<7)G(G) T (p+I+g+)-результат очень похож на результат, полученный в n°344,3). На самом деле, это делается в более общем предположении: p>0,<7>0, g>0. Но когда функция парциальной плотности становится бесконечной (например, в 0<p<1 мы проходим плоскость x=0), Интеграл уже «неуместен» и требует дополнительных маргинальных переходов. Определение такого интеграла строится таким же образом, как и для двойного интеграла[см. n°344,4].
Смотрите также:
Решение задач по математическому анализу
| Упорядочение множества бесконечных десятичных дробей | Принцип локализации |
| Операции над множествами | Существование точных граней |

