Преобразование плоских областей

Оглавление:

Преобразование плоских областей

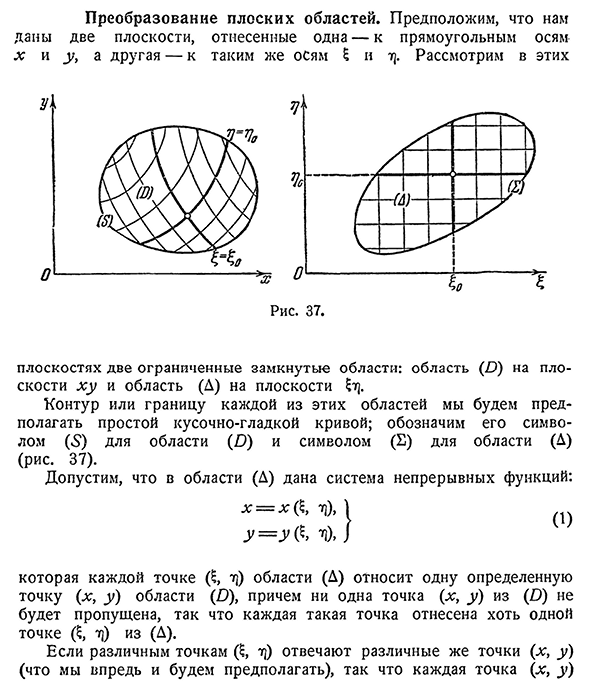
Преобразуйте плоскую область. Один из них присваивается прямоугольным осям x и y,а другой-тем же осям B и T. рассмотрим эти область ( / ) на плоскости x и область (A) на плоскости B]. Предположим, что контуры или границы каждой из этих областей являются простыми кусочно-гладкими кривыми, и обозначим их знаками области ( / ) (5) и знаком области (D) (E). 37). Предположим, что в области (E) задана система непрерывных функций: х=х (6,х),|

г=г&г), ) В какой точке (в какой?}) Области (D) означает определенную точку (x, y) области (O), и точка (x, y) области (O) не пропущена, поэтому каждая такая точка делится по крайней мере на одну точку ( ^ , t) области (D). Для разных точек (^,?}) Встречаются одни и те же различные точки(x, y) (предполагая в будущем), и каждая точка (x, y) 352]§5. Замена переменной в интеграции 275x Назначается только одна точка ($,?}), Уравнение (1)

однозначно разрешимо относительно&и C: переменные 5, t]являются очевидной функцией области (L) x, y) Ч=м),| 7]=7](Х, Y). / (1А) Таким образом, Людмила Фирмаль

устанавливается взаимно однозначное или взаимно однозначное соответствие между областями (Р) и (А). Также сказано, что выражение (1) преобразует домен (a) в домен (P), а выражение (1A) обращает домен (O) в домен (A). Подчеркнем, что необходимо, чтобы точка контура (2) соответствовала точке контура (5), и наоборот. Кроме того, предположим, что функция(1) не только непрерывна, но и (A) имеет непрерывные частные производные первого порядка. И

функциональные детерминанты ДХ у) де я&ч) Дуду}д~д^\ Существует ли непрерывная функция?t] область (A). Поскольку этот определитель всегда отличается от нуля, предположим, что непрерывность имеет постоянный знак. Это предположение играет важную роль в будущем. Если взять простую кусочно-гладкую кривую (A) в области (A), то с помощью преобразования (1) получим аналогичную кривую (L) в области (f). Фактически, мы делаем уравнение кривой (L) следующим образом: ‘1=t) (0(a i p или A P), (3) и (если вы хотите ограничить GL A k и m кусочками кривой), функция C^),?} (0 имеет непрерывной

производной,о б р а Щ Ай Щ и Е СИА о д Н О В Р Е М Е Н О в ноль. Подставляя эти функции в Формулу преобразования (1), получаем параметрическое уравнение (L) для соответствующей кривой): X=X0 (O>7) (^)=X (0 , (4) 276CH. XXT двойной Интеграл[352 Легко видеть, что эти функции также имеют непрерывные производные: /Я(5 ) У( 0 = | * ‘ ( 0 + ^ W Это также не может быть обращено к нулю одновременно, поэтому на кривой(A) нет специальной точки. На самом деле, если не считать неравенства детерминант до нуля, то из(5), в то же время,’=0 и

t’ — 0, что противоречит предположениям. Если точки (5,?}) Описать z на плоскости M K n u T Y-го контура (A), например, в положительном направлении, соответствующая точка(x, u) также объясняет некоторый Zam k-го на том же контуре (a) плоскости этот вопрос, Как видно ниже[n°35,4,1°], зависит от знака функционального матричного уравнения. Задает пару значений переменных. (D) в области [$t]однозначно идентифицирует конкретную точку в поле(/?) В плоскости XY, и наоборот. Это дает основание называть число t] координатами ( / ) точек области.

Кривая, состоящая из точки в области (O), где одна из координат имеет постоянное значение, Людмила Фирмаль

называется координатной линией. Например, предположив в(1)7]=t] 0, получим p a m e t I h S K o p E R e d s t a в координатной линии: х=х($,•%),г=г&^о) (Здесь роль параметров играет). В том же ряду n o e u R a n e N I e, мы можем получить его, предположив 7|=t] 0 уравнения (2): 7](x, y)=^. В связи с тем, что координатные линии становятся, в общем случае, p и b y m, числа B и C называются криволинейными координатами точек, характеризующими положение точек на плоскости XY. Если мы дадим координате t] другое (возможное) постоянное значение, то получим целое семейство координатных линий на плоскости XY. Если вы измените значение координаты 5, вы

получите другое семейство координатных линий. В присутствии один к одному 352]§5. Замена переменных в двойном Интеграле 277 Различные линии одного и того же семейства не пересекаются друг с другом, и одна линия из каждого семейства проходит через любую точку области (I) и рассматривает соответствие между областями. Вся сетка координатных линий на плоскости X-y представляет собой изображение сетки линий$ = sopz1 и t]=sopz81 на плоскости (рис. 37). 1) Самый простой и важный пример криволинейных координат-полярные координаты g, 0. Они имеют четкую геометрическую интерпретацию как полярный радиус-вектор и Полюсный угол, но

могут быть формально введены с помощью известных соотношений: Х = поп г 0,г=G81P0. Если значения G и 0 откладываются вдоль двух осей, перпендикулярных друг другу, например, G-абсцисса, а 0-ордината (правильная ориентация оси), то по указанной формуле вычисляется половина g0. Читатель должен был иметь дело с соответствующими координатными линиями:прямая g=sopzx-это окружность радиуса g с центром в начале и прямая 0=sopz! сигнал, излучаемый с самого начала под углом 0 по оси x(рис. 38). Но гораздо

больше Лучи угол 0 × 2/ГХ(где K является целым числом) не влияют на значения X и Y. Чтобы получить все точки в плоскости XY, достаточно ограничить значения В этом случае Формула преобразования не может быть решена вообще. Каждая точка (x, y), в отличие от первой, соответствует одному значению g>0 и одному значению O в пределах заданного предела. Но непоправимое нарушение единственности соответствия связано с началом координат: точка x=y=0 является отрезком всей оси 0 (или, при необходимости, от 0=0 до 0=2K).） Рассмотрим замкнутый прямоугольник в плоскости

G0[0,/?; 0,2 ТС]или оофу (рис. 39); в плоскости xy легко видеть, что радиус D=OA отвечает замкнутой окружности, нарисованной вокруг начала O. Но весь контур этой окружности соответствует только стороне указанного прямоугольника. Наконец, вся сторона 07 ответа o только точка, здесь явно не соответствует этим в условиях предыдущей задачи!278 главы XXI. двойной Интеграл[353 Однако, если вы сдвинете сторону 07 с небольшим значением p=OEG и сдвинете сторону 7 С e=P0′, вы получите новый прямоугольник 2) иногда это удобно o’AR ‘ 7 ‘отвечает на плоскостную фигуру Xu O ‘AV’, полученную

из окружности путем удаления малого круга радиуса p и сектора центрального угла e, в соответствии со всеми требованиями. При перемещении точки на плоскости отрезки G0 являются’, ru, 7′, 0′, o’A, а соответствующие точки плоскости описываются в порядке XY: неполный круг AB'(радиус/?), Сегменты B\неполный круг C’o'(радиуса p) и сегменты O’a. Обратите внимание, что положительного обхода на плоскости ехать соответствует положительный обход в плоскости XY. Функциональными детерминантами в данном случае являются Р (Х,Y)1 0 поп-G81P0I п(г,0) / 81P00G поп-0 г * Он сохраняет

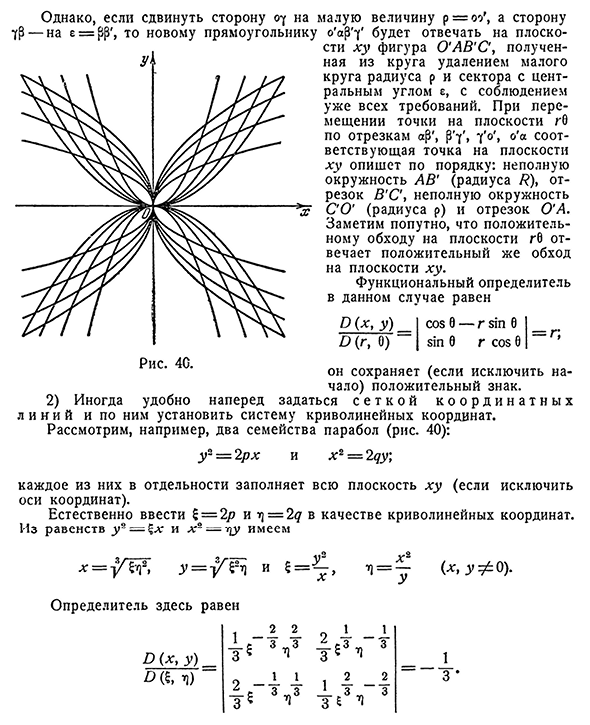
положительный знак (За исключением начала координат), и сначала находит е т К О Й К О Р Д и Н А Т н ы х л н и й, и устанавливает криволинейную систему координат. Рассмотрим, например, два семейства парабол. 40): y2=2px и x2=2du;каждый из них заполняет всю плоскость XY (исключая координатные оси) отдельно. Естественно ввести^=2P и^=2^в качестве криволинейных координат. Уравнение y2=%x и x2=t^имеем (х, udyo). Определяющим здесь является Р(Х, Y) Три. *

Связь с вопросом о точном дифференциале	Выражение площади в криволинейных координатах.
Приложения к физическим задачам	Дополнительные замечания