Оглавление:
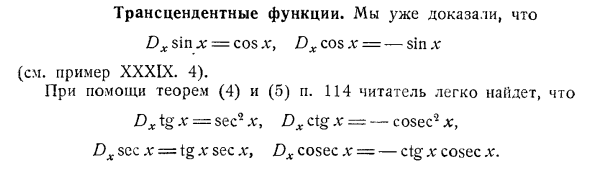

Трансцендентные функции
Трансцендентальная функция. Мы уже доказали это Dx sin l: = cos x, Dx cos x = -sin x (Пример XXXIX, см. 4). Используя теорему (4) и (o) в стихе 114, читатели могут легко найти ее. Dx t g .v = sec2 L ‘, Dx ctg x = -cos it * x, Dx sec x = tg x sec x, Dx cosec x = -ig x cosec x
Теорема (7) позволяет легко найти производную обратной функции циркуляции. Читатель должен проверить следующую формулу: Dx arc sin x = zh. , Dx arc cos l: = 1 ^ arctgArrrry ^, Z) ^ arcctgA: = —j-p ^, D .arc sec * = ± — / * ■ -, Dx arc cosec x X Y ^ X * -1 * * dgu ^ -Г
Это легко вывести из теоремы (6) и (7) в разделе 114. Людмила Фирмаль
| Дробно-рациональные функции | Некоторые общие теоремы, относящиеся к производным |
| Алгебраические функции | Максимумы и минимумы |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Для функций arc sin x и arc cosec x берется знак, соответствующий знаку cos (arc sin x), а для arc cos x и arc sec l * знак совпадает со знаком sin (arc cos x) Я сделаю это Следующее более общее выражение также очень важно: Z ^ arc sin — ===: £ _! =, Dx arctg — == L а х а х * — \ — а **
В первом разделе знак cos (arc sin так Ci как В зависимости от того, положительный он или отрицательный. Наконец, теорема §114 (6) может использоваться для различения комплексных функций, которые состоят как из алгебраических, так и из тригонометрических функций.
Следовательно, вы можете вычислить производную функции, как показано в следующем примере. Людмила Фирмаль

