Оглавление:
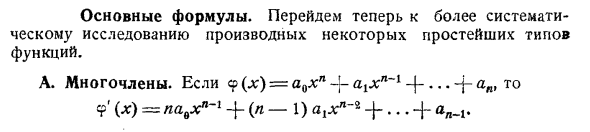

Основные формулы
- Основная формула. Далее мы переходим к более систематическому изучению производных некоторых простейших типов функций. А. Полином. 9 (. *) = A0 * n -j- a ^ x * Если «1-f- •• + ay», 9 ‘(*) = pa, * — * + (n-1) в! * «» «+ … + ay_ |
Может быть более удобным использовать многочлен степени n по x в так называемой биномиальной форме a0x «+ (*) a, *» — + [I) a, * -‘-} -… + a „. B в этом случае = n je ^ — + (l 7 ‘) * + («7’) + — ■ • ■ +} •
Бином 9 (x) часто записывается символически следующим образом *): (A0, al9 …, и 9 ‘(l-) = 1 (a0, I) 71 «1. Людмила Фирмаль
| Производные комплексных функций | Дробно-рациональные функции |
| Обозначения дифференциального исчисления | Алгебраические функции |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- В будущем мы можем видеть, что многочлен y (x) всегда можно выразить как произведение n факторов. 9 (• *) = aQ (x-ar) -a2) …- an) 9 А является реальным или сложным. тогда (■ *) = Luo) ~~ -az) ••• —O »
Кроме того, это сокращение означает, что все возможные продукты формируются из n-1 элементов и добавляются. Этот результат действителен, когда некоторые числа a равны друг другу. Затем некоторые термины справа повторяются.
Читатели легко это устанавливают 9 (x) = a0 (x-a,) из 1 (x -… … (x-av) mv, к 9 ‘(x) = a6U ^ tu (x-a1) Wl «1 (- *» — «» A- •• (* — «v) m *. Людмила Фирмаль

