Переходные процессы теплопередачи

Переходные процессы теплопередачи

• В предыдущей главе рассматривалась такая система, в которой процесс изменения температуры во времени завершается в результате теплопроводности. Теоретически. Требуется значительное количество времени для установления устойчивого теплового потока и устранения эффектов переходных процессов на границе системы. Этот раздел является Процесс j для нагрева или охлаждения объекта, то есть так называемый процесс миграции (₍ ₍ ₎ ₎I process. Сплошной Бесконечно большая теплопроводность. Если есть очень большое тепло риса на теле.

4-1.Равномерная проводимость и низкий коэффициент теплообмена и теплового потока к телу Со стороны тела определяется в основном конвективным сопротивлением, небольшой градиент температуры возникает в теле или полностью отсутствует, то есть тело пространственно Изотермическая, температура меняется только со временем. Некоторые небольшие объекты с ограниченной теплопроводностью отвечают вышеуказанным условиям.

To вызов В зависимости от характеристик системы, она заключается в определении изменения температуры с течением времени. Людмила Фирмаль

Подумайте о маленьком диске (Диаграмма 4-1), температура в форме medium. At в какой-то момент температура была помещена в другую жидкость или газ streams. Запишите уравнение теплового равновесия диска: (4-1) уравнение (4-1) V- Объем диска и L-это площадь поверхности. Соответствующее начальное условие/ = / ₀ равно m = 0.

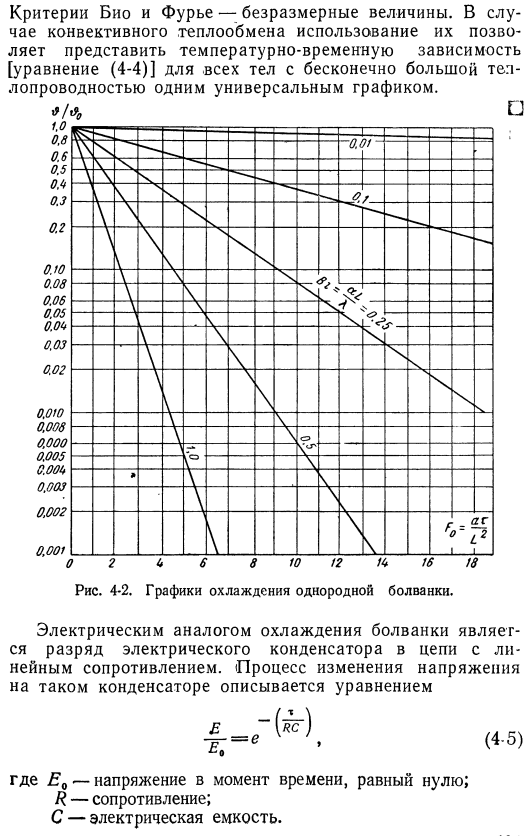
Температура окружающего потока (tf) постоянна. Формула (4-1) Дифференциальное уравнение избыточной температуры, 0 = Z-tf: _ aA b pcV d’z. используем граничное условие m = 0 для получения решения уравнения (4-2): Форма:&_ _ (vL / rgk) tл (4-3) графическое представление уравнения координат 1n & / & ₀ (4-3) от m, aA / pcV Параметры. Формулу (4-3) можно переписать в более удобную форму. Джей- = ₑ-(ал / Х)(У / Л’) (4.4)где е / —это стандарт био. Ayl * — критерий Фурье. — Коэффициент термической диффузии. Соответствующий график в Формуле(4-4) в & & & АЗ [L2 и его зависимость в качестве параметра(рис. 4-2).

Значение L в Критерии био и Фурье представляют собой характеристический размер системы и определяются как отношение объема тела к площади поверхности. Поэтому самая простая геометрия Легко получить значение L в следующем виде: шарик 4 / 3eg§ 3 «цилиндр L 2kg0 / 2 Z Go» куб L-11-1 6/2 6 * Критерии био и Фурье безразмерны quantities. In в случае конвективного теплообмена его использование позволяет выразить зависимость температуры и времени[Формула (4-4）] Для всех объектов с бесконечно большой теплопроводностью в 1 универсальном графе. □Рис. 4-2.График охлаждения однородного диска.

Электрическая реакция на охлаждение дисков Это разряд электрического конденсатора в цепи с линейным сопротивлением. Процесс изменения напряжения на таком конденсаторе описывается формулой£ _ _ («с) (4-5).Здесь.、 Eo-это напряжение в момент времени, равный нулю. R-это сопротивление. C является электрическим capacity. By эта аналогия, цепь R, C、 Моделирование переходного процесса теплообмена. Пример 4-1.При измерении переменных температур с помощью термометров важно знать, как быстро термометр реагирует на изменения Температура. Полупериод — это временной интервал между начальной разницей между истинной температурой и показаниями термометра. Истинные внезапные изменения в temperature. It необходимо определить этот полупериод ртутного термометра в потоке воздуха.

Пусть шарик ртути будет в форме цилиндра Радиус 3 мм. теплопроводность ртути составляет A = 7,45 kcal1m’h-град(см. Приложение).Температуропроводность a = 0.0166 mg1h, сопротивление жары тонкого Проигнорировал стеклянную стену. Коэффициент теплопередачи воздушного потока a = 50 ккал / м2-ч-град. a. L-50-0.003 следовательно, биостандарт — ₇₄₅ > 2 = 0.01. формула для соотношения b (4-4） Если число в индексе равно 0,693, то оно будет равно 0,5.Таким образом, формула для определения периода полураспада становится(axH /L2), следовательно характеристика Размер: 0.693 L2-0.01 „69.3 и пол: y продолжительность: 69 3-9-10“ ⁶X /7⁼-OT66 ^ _ _ SEC ’3⁶⁰333′ SEC SEC ’ показания термометра.

Если это изменение происходит с меньшей скоростью, оно правильно отражает истинное изменение температуры(в случае изменения температуры синусоидальной волны период обнаружения равен 10 Более чем вдвое [Л. 19]).Бесконечно большая жара емкости твердого тела-О. Граничное условие является функцией времени. Рассмотрим диск, показанный на рисунке. 4-1, температура Температура потока изменяется линейно со временем от нуля. То есть температура потока определяется по формуле: (4-6) формула (4-1), если происходит изменение Температура потока: d /. Л. А. . An dv ’ pcV » pcV (4-7) уравнение (4-7) решение принимает вид:/ =(4-8）.

Константа C может быть оценена из начального условия, которое предполагает нулевое начальное значение temperature. So, общее решение принимается следующим образом Вид: t = Bt-B [1 — e — ^ fCV}]. (4-9) уравнение (4-9) показано на рисунке. 4-3.Вы можете видеть, что температура пластины всегда позади Жидкость temperature. As как только явление перехода исчезает, ковер становится постоянным. Это можно сделать из очень емкого уравнения (4-9).Термометр от Используйте пример 4-1 для управления температурой обычного stove. It необходимо рассчитать задержку термометра при нагревании печи со скоростью 204 градуса З / ч коэффициент теплопередачи а = 9.8 ккал / м ^ — ч-град.

В данном случае, ₉cV rQX _ 0.003.7.45 объявление 2размера 2.0.0166-9.8″ •Д / = 0.08-204 = 16.32°C. бесконечно большие плиты. Проблема переходного процесса теплопроводности в системах с пространственным распределением температуры является весьма актуальной Громоздкие и сложные математические расчеты. Фурье. 20]мы разработали известный метод рядов Фурье для решения этой проблемы. «С пластиной толщиной I в направлении x если тепловая конвекция теряется на поверхности x=/, то теплопроводность в отсутствие источника тепла уменьшается до DXA. dh2где & — избыточная температура любой точки тела. Пластина показана на рисунке. 4-4.

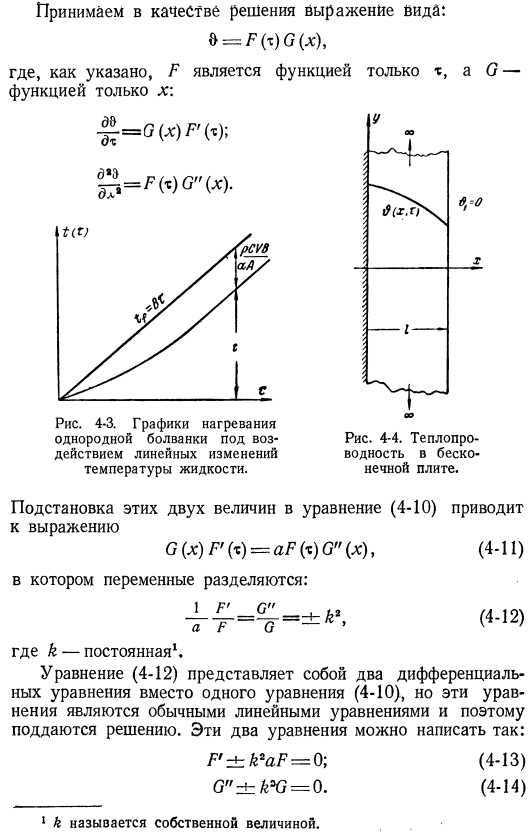
Это уравнение может быть решено для многих граничных условий методом разделения переменных. В качестве(4-I) изо-(4-I) решения уравнения теплопроводности возьмем уравнение следующего вида: O = F (t) G (x), где, как показано, F — функция x \только M, a G — ^ = G (x) f’w; рис.4-3. График, который нагревает однородную свинью под влиянием линейного изменения температуры жидкости. ОО рисунок 4-4.Теплопроводность бесконечных пластин. Эти 2 замены Значение формулы (4-10) приводит к формуле G (x) F ’(t)= aF (t) G «(x), (4-11).Где переменные разделены:(4-12) где k-Константа 1 выражение (4-12） 1. представляет собой 2 дифференциальных уравнения, а не 1 уравнение (4-10), но эти уравнения являются обычными линейными уравнениями, поэтому их можно решить.

Эти двое. Уравнение можно записать так: F’ztfc#aF = 0; G «ztz /e3G=: 0.(4-13) (4-14) 1k называется собственным значением. Решите уравнение (4-13), и вы получите T: F =Cₓe^ ax. Избыточная температура со временем снизится, но примет знак минус. Если вы решите уравнение(4-14) с отрицательным k2, вы получите G =C₂e+ⁱkx+C₃e〜ⁱkx. Конечно, полное решение 0 = 7? (х) г (х), следовательно,& = Е К недорогой(4cos грехов кх кх). (4-15) граничные и начальные условия: g -=°, x = 0; (4-16） £•— * = ’•（4-1 ба)8 = » 0, М =0.(4-166) по существу, 3 константы A, B и k должны быть определены. Следовательно、 3 требования к determination. In формула (4-16), производная db / dx = 0 требуется для x = 0 ^ L = e-k, ax(-i4,^ sin kx — \ — Bkcos kx). (4-17) формула (4-17) из, B.

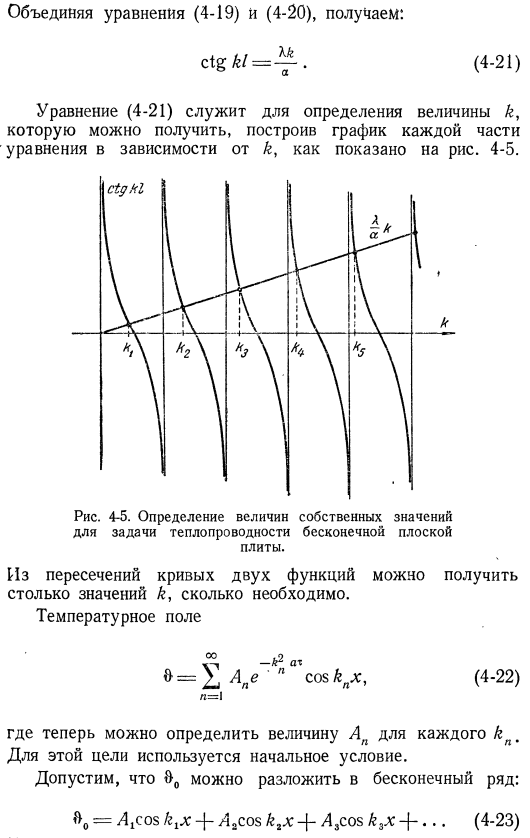
 Он должен быть равен нулю, чтобы градиент температуры (d & / dx) x = O. получим решение H = Ae-k’AX cos kx. (4-18) 2-е граничное условие、 Вы можете использовать формулу(4-16a) для определения K. (4-19) выражение (4-18) из 0 / = Le *2flTcos&/. Если объединить (4-20) формулы (4-19) и(4-20), то получится следующая формула: (4-21) формула (4-21) используется для определения значения k. это может быть получено путем построения каждой части выражения в виде функции k, как показано на рисунке. 4-5.Рис. 4-5.Определите количество Собственное значение задачи теплопроводности бесконечной пластины. Из пересечения кривых 2 функций можно получить значение необходимого числа к. температура Поле COSkₙx(4-22), где можно определить значение AP для каждого K для.

Для этого используются начальные условия. Предположим, что вы можете развернуть его в бесконечном ряду:= / IjCoskₜx4 — / i₂cosk₂x4-4₃cosk₃x4×4〜… Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь обращаться к нам»cos k x cos kx dx = 0, j m n tn 0, если m ^ n. остальное. Значение i J t>₀coskₙxdx= JЛ^ *kₙdx, оо позволяет получить константу an. Таким образом, 29₀ sinkinksnl kₙl+ sinkₙllcoskₙl (4-24) для удобства предположим kₙ= bjl и получим формулу для конечного распределения температуры: (a//) 20ₒsin3ZJcos (dᵣₜx//) ^ + sind » cosdₙ (4-25) теплопотери полубесконечной пластины получены из закона .

Фурье теплопроводности (DX ₌ I V P-B ^ а!、 ’⁾______________ V * L = /1L + sin d » cos8n•, когда Формула (4-26) подставляется в закон теплопроводности Фурье, то Qi _ 2M>. 積分qᵣг-I jzj3ₙ + Sin» » cosaₙ•0 интеграл уравнения n = l (4-27) (на ней показан тепловой поток района Ацута.(4-28)σ, включая характеристический индекс KK(4-21). , 4 = VSV(4-29) можно писать крупно. 8ε=Ε^(ε) уравнение № 4-26), (4-28) и (4-29) решенный результат показывает, что группа функций_ f (ahh\ «» FTJ; kw (±L. a/s） \l’i* ’ y ’Qi_c / ala -qqo» ’A*’ R / эти результаты показывают, что Гребер[L. 21] и Гурни Лу[L. 22], его Лер ом[L. 23.].

Другие за другими. Аналогичное решение получено для большого кольца и шара. Игра бесплатная! Это 3 из 1 из одного решения.4 из большего формата Nomo ragged-6-4-8 Значение переменной. Решение двух-и трехмерных задач problems. In в большинстве случаев задача нестационарной теплопроводности включает прямоугольный параллелепипед или короткий 017.In в этих случаях они не могут применяться непосредственно. А. Б. Ньюман.24.] Решите одномерную задачу, в которой есть решение, в двух-и трехмерной. 2-D метод может быть использован для решения 3-D легко.

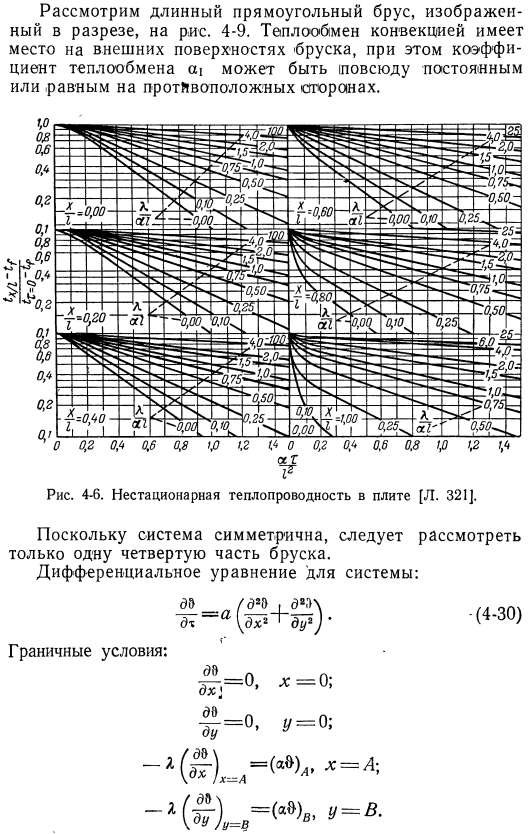
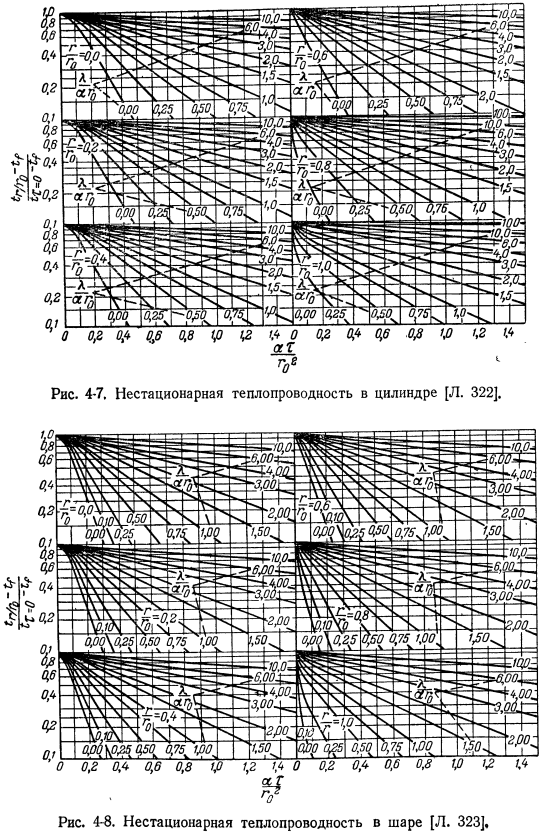
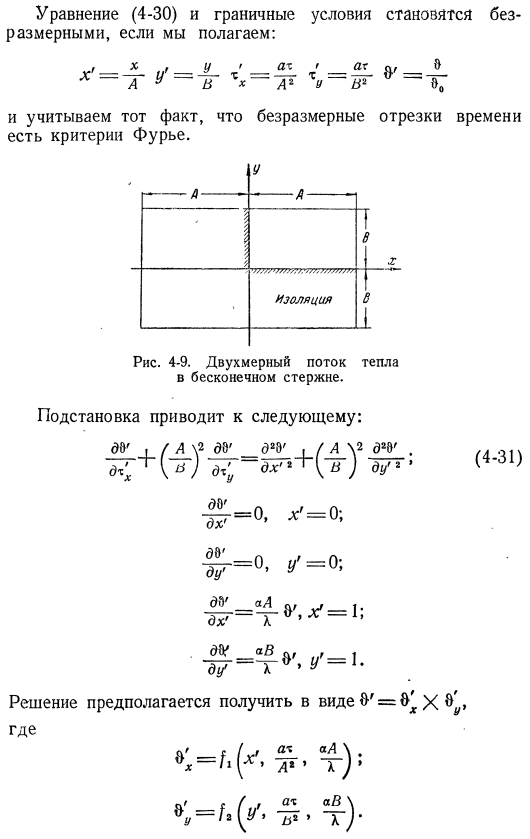
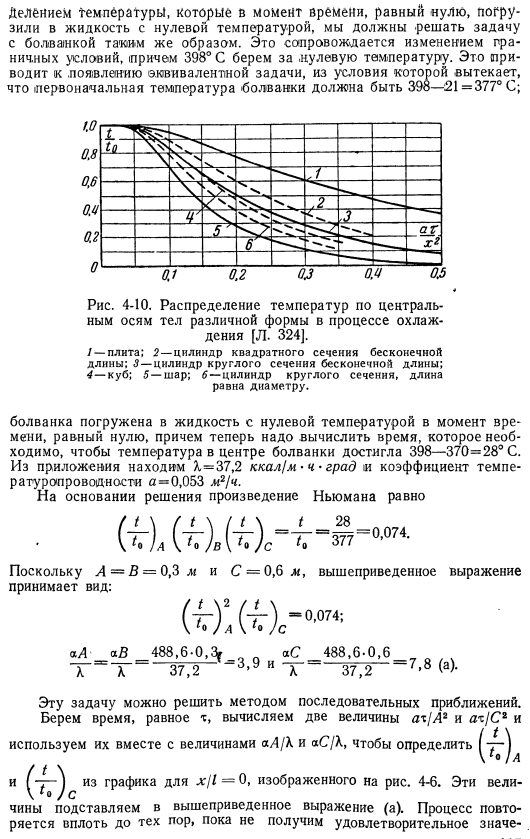
Следующий. Давайте посмотрим на длинный прямоугольный биом, показанный на рисунке. 4-9 конвективный теплообмен осуществляется с обратной стороны, но Термообработанный он может находиться в любом постоянном месте 4-6.[Л. 321].Поскольку система нацелена, она должна быть нацелена только на 4 минуты до 1. 。- Из. 。 Минутное уравнение уравнения системы: y-c. (4-30)4747.017 константа-устойчивый коэффициент теплопередачи в считывателе[L. 322].Рисунок 4-8.Постоянный коэффициент теплопроводности шара [Л. 323].Выражение (4-30) и фраза безразмерны, если вы определяете: X’GBN’、0— ^ = 1 = \ = = = = — есть 9i.

Это хорошая игра.- Что? Л н-л н д — — — — — — — -. \1[¶ Изоляция рис. 4-9.。Поперечный тепловой поток в кус-куспе. Следующее, что вы увидите：00 ’<4 2 00′ 028 ’0х’ 00’_P ДХ’ — о、 00’=0du ’ 00 ′ aA0X’A0O>aH, 0 / X / =1. (4-31) do «’решение должно быть получено в виде 0′ =0 * вставьте описанную форму в Формулу (4-31) 1 / Д2 1д ы — <м о;1DCH’х/Д Х2 1dch0^ДХ ’2В)сделать’2（4-32）（（4-32） （ли FDX по, Х)=ф^(г, м)=0.Есть 2 академические формулы. E ’d’(4-33) метод уравнений(4-33)является бесформенной формой метода уравнений (4-10) и имеет решение, аналогичное решению. Формулы(4-25)и(4-28).Поэтому из области решения бесконечной пластины толщиной 2 » 24 и 2.

B ясно, что решение содержит опорное одно бесконечное поле. 2AX2B. легко предположить, что параллельная плоскость с чтением 24×2bx2c может быть решением для каждой из 3 бесконечных пластин. 24, 2В, 2С. Рис. 4-10 показаны линии объекта с грубой форме. Конечным является температура M>0 в прошлом, » поверхность сразу же сохранялась в r>=0[L. 25].Многие другие решения могут быть найдены в книгах carslow и Jaeger[л. 26] Шнайдер[л.27]и мак-Адамса[л. 28].Пример 4-3.In термообработка в пресс-форме в пресс-форме В случае закона 0. 3×0.3X0.6m необходимо нагреть все части заготовки до 370°C, но температуру любой части заготовки следует считать равной 398°. C.

 To для создания этих условий заготовку с начальной температурой 2°с помещают в печь и циркулируют в инертной атмосфере при температуре 398 ° С. Эд.、 Тепловой коэффициент 788 6ккал↑м2•ч-градуировка. Достигает ли температура заготовки 370℃?Полоскать По существующим условиям решения, применимым только для твердых тел с равномерным начальным распределением, эти 2 величины должны быть равны константе. Просто нажать、 Уравнение должно быть равно постоянному нулю, потому что оно должно быть в отсутствии другого equation. By диспергирование температура должна быть жидкой в момент нуля .

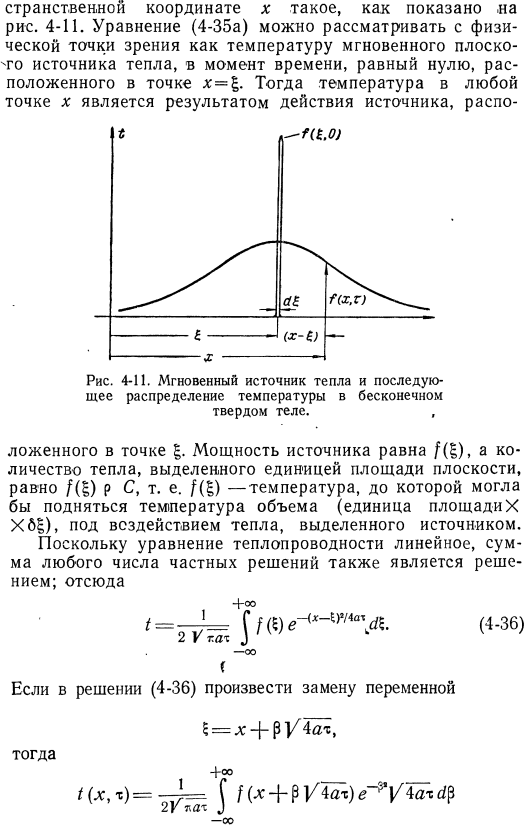
• Если температура Лоло, то диск нужно анализировать точно так же.。 4-10 ″ классификация температуры в контакте с осью в центре целого». [Л. 324]. / — Средний носок; 2-правой формы поперечного сечения необрезной длины. 。 3 -.Вертикальная длина горизонтального сечения. 4-Кук. 5-мяч. 6-галлеандр Sehwan, длина равна прямой линии. Заготовка будет находиться в точке температуры, равной температуре рулона в жидкости Ролло. И вам нужно рассчитать необходимое время. Температура 19398-370=28°C внутри диска сканирования и запаха. Из приложения, X=37,2 ккал}м * ч * 玻 満 и тепловое расширение = 0. 053м2 / ч.

На основе определения Поскольку произведение Ньюмана равно ( ^ ) s≦7G;^(θ°)≦°(t) l (7r)-A=B=0, 3m, C = 0.6 l, приведенная выше формула является aa aB488. 6-0, ЗГ л aC488. 6-0. 6_,. XY 37.2 X-37.2 3⁹ и X⁷⁸ < a «target =» _blank » > — эта задача может быть решена методом последовательного приближения. вычислите время, равное t, вычислите 2 величины dt / D2 и Dt / S2、 Используйте их со значениями/X и A, чтобы подтвердить u^7 ″ ^из графика на рисунке xjl=0. От 4 до 6 (поставить в Формуле (а)выше значения А и. Это позволяет вам очистить вверх. а)Soton. It это здесь, это в твое время, здесь, здесь, здесь, здесь, здесь 370°C.

Тогда точка x температуры источника является результатом поведения твердого тела, которое является источником. Людмила Фирмаль

У нас есть широкий выбор по отличным ценам, чтобы помочь вам получить творческий подход. 。 t определяется как 1,53 часа. П0..053.1.53 0.09 0.225; = 0.125。 0.053-1.53 Рисунок 0.36°4-6for l/ / =0 (фигурные скобки для каждой пластины) применяется значение параметра. Поэтому、（0.302）2（0.805）= 0.0735、то есть время, необходимое для поддержания температуры Внутренняя крышка диска была закончена при Tata=l, нижняя правая установка при 53 часах до 370°C. Если m>0, запросите характер содержания твердого вещества x = 0 в середине, hoehold-это выражение/= / (% ).

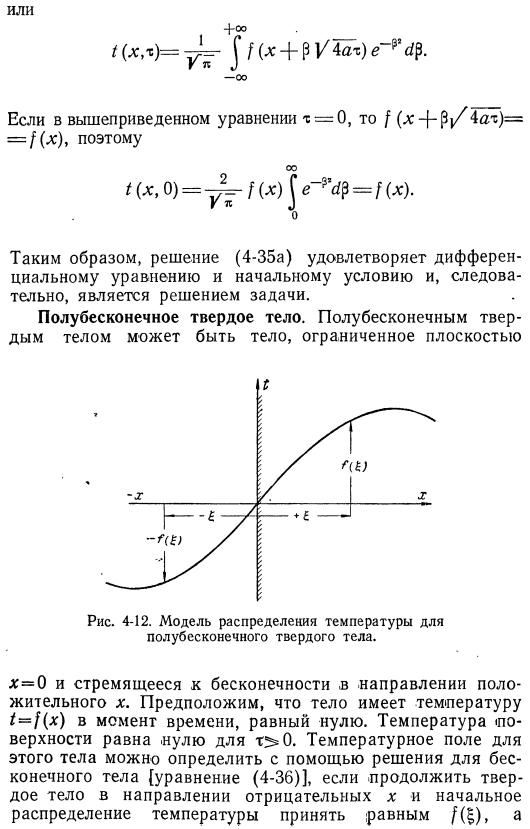
Уравнение-a dx•(4-34) решаемое уравнение классифицируется относительно-x*/4ach>(4-35). 1 x по отношению к 2 раза-не забудьте ввести в Формулу (4-34), чтобы заполнить уравнение полностью. Большой (4-35) (, в небольшой формуле. Это также решение минутного уравнения: t= — pLe — (4-35A), где$ — параметр. Это выражение обладает тем свойством, что теперь оно равно ( * ) в любом месте. поверните случай x=£, Lolo good time (( = )). если увеличить значение m, то температурное поле x будет: Рисунок 4-11.Уравнение (4-35А) , с физической точки зрения, плоскостью мгновенной можно считать температуру источника тепла (в момент, равный нулю, находящегося в определенной точке икс.

Я вижу это в точке g. выход источника равен f ( £ ), количество тепла (F (g) pc), который будет выделен единицей площади G. То есть f(g) — это температура, при которой объемная температура (отношение площадей X6G) повышается под действием продукта тепла. Источник и выделено. Поскольку тепловая формула линейна, она представляет собой набор конкретных решений из числа композиций. Здесь<или < =7Ф（ «） е^ — в WTA\Ди. (4-36)2V Toms J-00 (Если заменяется изменение Tsushin (4-36)τ 4-00___2то пах Джей-00 (Ладу+ОО т(х, р) = р(х+Пи/4^)е^’д^. — 00. Т(х, 0)=г= — Ф (Х)^е-^=ф(х).

И тогда, ((4-35A)было уравнение уравнения. Государство. Один твердый предмет. Полубесконечное твердое тело становится телом животного, заключенным в плоскость. 4-12. Модель распределения температуры бесконечного тела. x=0π, и существует положительное направление x в направлении Бесконечности. Размер (х) 。Хорошее время. для m>0 температура поверхности равна Lolo. Температурное поле этого объекта может быть определено с помощью бесконечного анализа объекта. (4-36)], продолжая твердое тело в направлении X ночью, если принять распределение ночной температуры равным^(g), x=0 редко встречается для 3 при холодных температурах. (Рис. 4-12).(4-36)Т = êtu{ЯФ(5)Ди+J и [- Ф(-{)]Е-^ ’ ^Ди\0■ — ОО — — — — -,-(х-кф/широта системе JDE.(4-37) когда .

Гекту одиннадцать. Решение (4-37) можно украсить, используя B=-x—2ft]|ax вместо 1-го имени 5=x-/ — ar и вместо 2-го имени. Любить специфический продукт решения X/2^xflV ax1j e — ^ — φ3-x-2 / ai (4-38) в таблице, к таблице к дисплею слова. Если выводится определение решения 4-1 (4-38), то решение бесконечного твердого тела Поверхность опирается на нулевой круг, тело объекта рассматривается при температуре γ / / стык. 。 х-<erf-2^топор. Тепловое набухание поверхности ET x=0 определяется следующим образом. решение \ dxjx≧udrop (4-36) может быть применено к корпусу для»сварки металла сварного шва между 2 коронками тяжелого материала».

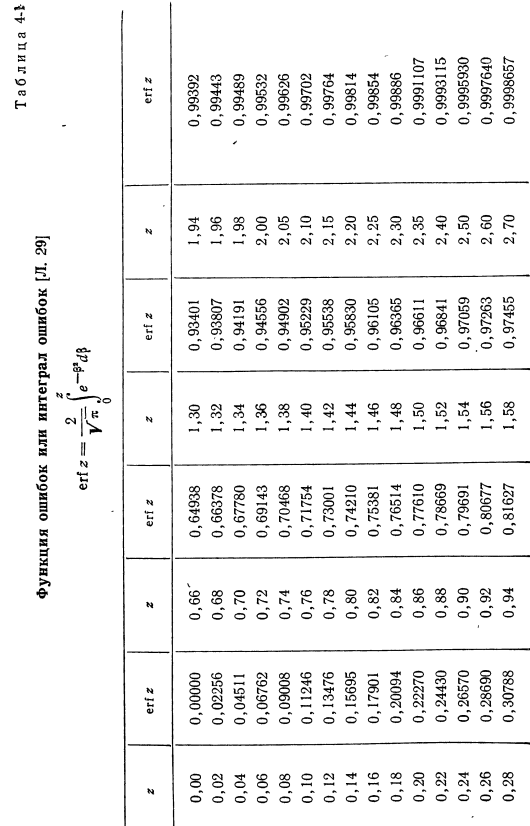
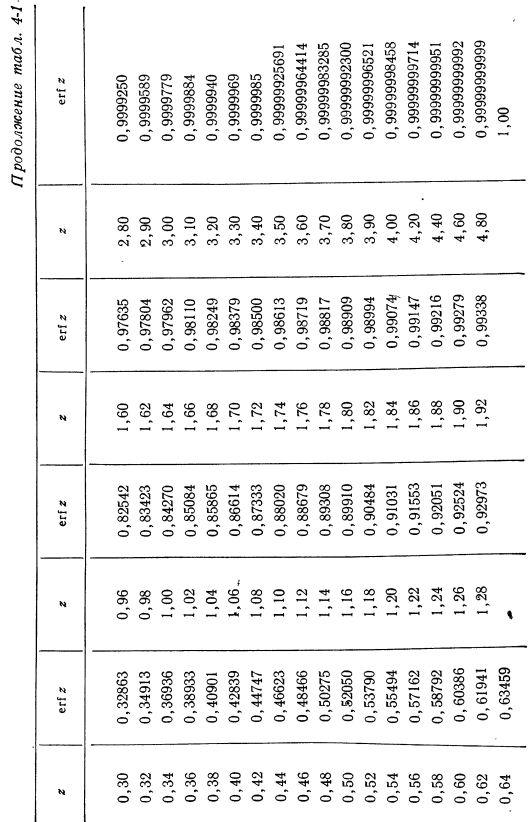
В. темпера — (4-39) (4-40) таблица 4-1. 29] erfz≒vfe.! Е В О З з з з з ФЗО ФЗО ФЗО 0.00 0.00000 0.66″0.64938 1.30 0.93401 1.94 0.99392 0.02 0.02256 0.68 0.66378 1.32 0.93807 1.96 0.99443 0.04 0.04511 0.70 0.67780 1、 34 0.94191 1.98 ’0.99489 0.06 0.06762 0.72 0.69143 1.36 0.94556 2.00 0.99532 0.08 0.09008 0.74 0.70468 1.38 0.94902 2.05 0.99626 0.10 0.11246 0.76 0.71754 1.40 0.95229 2、 10 0.99702 0.12 0.13476 0.78 0.73001 1.42 0.95538 2.15 0.99764 0.14 0.15695 0.80 0.74210 1.44 0.95830 2.20 0.99814 0.16 0.17901 0.82 0.75381 1.46 0.96105 2.25 0.99854 0、 18 0.20094 0.84 0.76514 1.48 0.96365 2.30 0.99886 0.20 0.22270 0.86 0.77610 1.50 0.96611 2.35 0.9991107 0.22 0.24430 0.88 0.78669 1.52 0.96841 2.40 0.9993115 0.24 0.26570 0、 90 0.79691 1.54 0.97059 2.50 0.9995930 0.26 0.28690 ’0.92 0.80677 1.56 0.97263 2.60 0.9997640 0.28 0.30788 0.94 0.81627 1.58 0.97455 2.70 0.9998657.

Таблица 4-1 з з з з з з ФЗО ФЗО ФЗО 0.30 0.32863 0.96 0.82542 1.60 0.97635■2.80 0.9999250 0.32 0.34913 0.98 0.83423 1.62 0.97804 2.90 0.9999589 0.34 0.36936 1.00 0.84270 1.64 0.97962 3.00 0.9999779 0.36 0.38933 1.02 0.85084 1.66 0.98110 3.10 0.9999884 0.38 0.40901 1.04 0.85865 1.68 0.98249 3.20 0.9999940 0.40 0、 42839 1.06。 0.86614 0.98379 1.70 3.30 0.9999969 0.42 0.44747 1.08 0.87333 1.72 0.98500 3.40 0.9999985 0.44 0.46623 1.10 0.88020 1.74 0.98613 3.50 0.99999925691 0、 46 0.48466 м2 0.88679 1.76 0.98719 3.60 0.99999964414 0.48 0.50275 1.14 0.89308 1.78 0.98817 3.70 0.99999983285 0.50 0.52050 1.16 0.89910 1.80 0.98909 3.80 0。 99999992300 0.52 0.53790 1.18 0.90484 1.82 0.98994 3.90 0.99999996521 0.54 0.55494 1.20 0.91031 1.84 0.99074-4.00 0.99999998458 0.56 0.57162 1.22 0.91553 1.86 0.99147 4 、20 0.99999999714 0.58 0.58792 1.24 0.92051 1.88 0.99216 4.40 0.99999999951 0.60 0.60386 1.26 0.92524 1.90 0.99279 4.60 0.99999999992 0.62 0.61941 1.28 0.92973 1.92 0。 99338 4.80 0.99999999999.0.64 0.63459 * 1.00.

При условии, что поверхность листа теряет тепло без каких-либо осложнений из-за изменения фазы Благодаря термической проводимости, задача может быть идеализирована введением t _ l__, так как она намного медленнее, чем тепло, которое течет в металл. t-o g t = 0 X——— 1 ——— J — — — — — — T — — — рисунок 4-13. Начальное распределение температуры во время 2 сварочных операций Лист.4-13 начального распределения температуры, как показано на рисунке. Это температурное поле указывает, что для x Z и x> m/ = 0, t =t₀ для 1 x m. можно записать решение、 Если формула (4-36) частично описана. Интеграл от /до m является единственным разделом, который дает дополнение./ = — (4-41)2 y выполните изменение переменной gro j.

Если вы перепишете функцию ошибки (m-x) J2 Y at = 77 J (/—x)/ 2 Y at или символ, вы получите следующее: 2 VaxJ (4-42) решение(4-42) Подходящее решение, но если η= 0 равноудалено от I и m, то B =(m-Γ) / 2\, то решение (4-42)выражается в терминах b как: (4-43) график Шмидта method. In много случаев Приближенный графический метод Шмидта[л. 30].Уравнение теплопроводности может быть преобразовано следующим образом Деление времени на интервалы Dm, деление толщины стенки(глубины) на интервалы Dx, уравнение конечных разностей с учетом изменения температуры этих интервалов (Рис. 4-14).

Формула для конечных разностей (от 4 до 34) имеет вид: Дт — (дх) 2 (4-44) индекс знака разности Y ’ — это время T или Координата x-разность D / при нахождении переменной. Интервалы между координатами и временем должны быть пронумерованы в order. So например, n (рис. 4-14) можно считать числом Любое расстояние между пластинами. k-число любого мгновения. Исходя из этого, значение D%/можно выразить так: D / = /.,- Т 。 t n, ky и количество ^tt=tₙ^ ^ ^ t-tₙₖ.Формула b2ₓt представляет собой разность между двумя последующими разностями. То есть, \n+.К ^ Н. к.） ^ nk ^ n -\, k)-Ci-H, k ^ n, k + ^ n-lk•если подставить эту формулу в Формулу (4-44), то получим:^ l⁼a » dx2^ l4-1l ^ n, k-V ^ l-i .Что?)- (4-45) i используя это уравнение、 (£- H) .

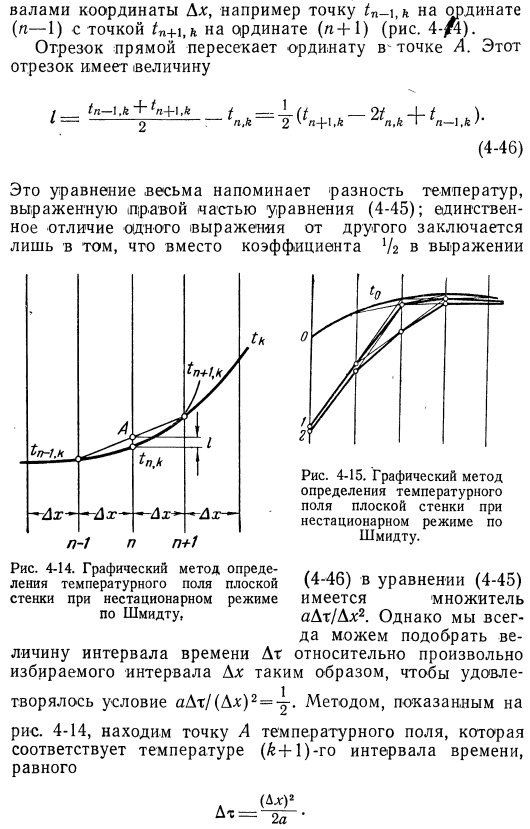
Температурное поле стенки на втором временном интервале (если распределение температуры известно на ( £ ) — ом временном интервале).На основе известного начального распределения температуры、 Применяя это уравнение последовательно, можно постепенно установить изменение температурного поля. Вместо аналитических расчетов можно использовать графические методы решения. Иллюстрированные фотографии. 4-14.На этом рисунке показана кривая распределения температуры для K-n временного интервала.2 точки температурного поля соединены прямой линией, разделенной двумя линиями Вал координат .

ДХ, например, ордината точки ТН -\, к (N-1) и ордината точки ФН + 1, Фе (/Р4-1)(Рис. 4-1).Отрезок линии пересекает ординату в точке A. Этот отрезок Кол-во/ _ _ + / — l_(t -<) / — \ — f——— 2 ———ⁿ ’ k-2 ^» 4-1Л⁴, 1N, k i LN-L, K) * •4-46) эта формула очень похожа на разницу температур. Он представлен правой частью уравнения (4-45).Единственное отличие одного выражения от другого заключается в том, что вместо коэффициентов выражения 4-15.Графический метод В соответствии со Шмидтом, нестационарный режим определяет температурное поле плоской стенки. В Формуле (4-46) (4-45) есть коэффициент яJt /Dx2.Но у нас всегда есть от 4 до 14.В игру очень легко играть.

Как определить температурное поле плоской стенки в нестационарном режиме по Шмидту, да, можно выбрать значение временного интервала Условие aDt /(Dx) 2=-^-DX произвольно выбирается интервалом, так что оно выполняется. Найти точку а температурного поля от 4 до 14 способом, показанным на рисунке. (£4-1) если вы соответствуете температуре второго временного интервала и соединяете другие точки температурной кривой, вы можете получить все точки температуры (k + 1) в поле второго временного интервала. Поэтому только этот метод используется для определения процента общего temperature.

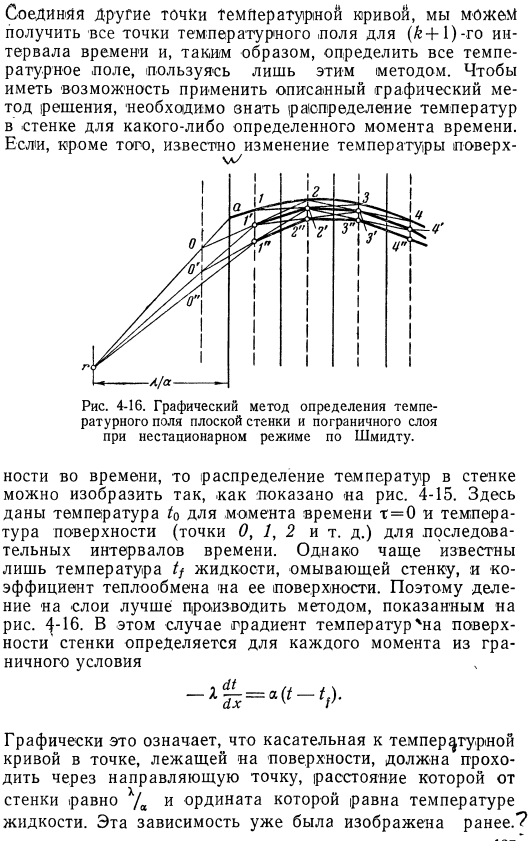
To уметь применять описанные методы графического решения, нужно знать Распределение температуры стены в определенной точке внутри time. In кроме того, если изменение температуры поверхности М / Л / А известно. 4-16.Графический метод Согласно Шмидту, нестационарный режим определяет температурное поле плоской стенки и границы layer. In время, распределение температуры стенок можно представить следующим образом Как показано на рисунке. 4-15.Здесь мы даем температуру для времени t = 0, а температуру поверхности для последовательных интервалов времени (точки 0, 1, 2 и т. д.).

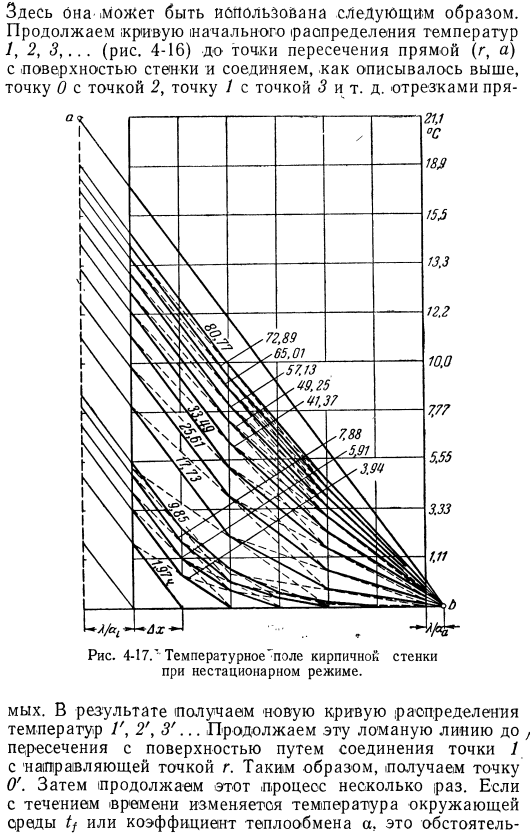
Но чаще всего Известны только температура жидкости, очищающей стенку, и коэффициент теплопередачи ее поверхности. Поэтому лучше разделить его на несколько слоев способом, показанным на рисунке. 4-16.So … В этом случае градиент температуры стенки определяется для каждого момента из граничного условия. Это графически означает касательную кривой температуры в точке Необходимо лечь на поверхность и пройти через направляющие точки, где расстояние от стенки равно х / а, а ордината равна температуре жидкости. Эта зависимость уже есть Предыдущее фото. Здесь вы можете использовать: начальная кривая ip продолжается и температура I, 2, 3,…также определяется до пересечения(рис. 4-16). Соедините линию (d, a) с поверхностью стены, как описано выше, точкой 0 и точкой 2, точкой 1 и точкой 3. 4-17.

«Температура» кирпичной стены пола Нестационарный режим. mykh. As в результате в случае новой кривой Р а также была определена температура 2’.Продолжите пунктирную линию, чтобы соединить пересечение с поверхностью. Точка / уставка r. So ты понял, в чем дело. Затем продолжите этот процесс несколько раз. Когда температура окружающей среды (tf) изменяется со временем Или коэффициент теплопередачи a. эта ситуация важна и может быть легко рассмотрена правильным движением направляющих, то есть вертикальных или горизонтальных точек. Здесь. 

1. простота обработки различных условий на поверхности является одним из преимуществ графического метода по сравнению с аналитическим решением дифференциальных уравнений. — Если граничные условия переменных вызывают математические трудности. Тогда это (этот метод, А. Несси и Л. Однородная система[L. 31].Пример 4-4.Они начинают отапливать гостиную с кирпичной стеной. Температура кирпичной стены изначально равна наружной температуре-1°с Определите период, за который устанавливается определенное распределение температуры в помещении и стенах.

Конечная температура помещения составляет 21°C. Внутренняя поверхность стенки а = 6 ккал / м2 * град -, внешняя АА, коэффициент теплопередачи= 14,5 ккал / м2 * ч * град; коэффициент теплопроводности а = 0,0011 м2 / ч; толщина стенки 0,396 м. распределение температуры стенки в режиме покоя задается прямой линией, соединяющей температуры-1 и 21°С, А и В. Поверхность стены на расстоянии X / a, и X / aa. Предполагая, что теплопередача к внутренней поверхности стены постоянна, в процессе нагрева Внутренний мир не меняется.

Теперь, чтобы начать графическое решение, мы разделим стену на 6 слоев толщиной Dx = 0.066 м. Отсюда мы найдем интервал. Времени (ЛК)* _0.0662 ДТ » — 2а 2-0. 0011-1, ⁹⁷h построение температурной кривой можно увидеть на фиг. 4-17.Как видно из рисунка, для установления стационарного режима необходимо Более 80 часов, то есть более 4 дней. Через 9,85 часа расстояние между координатами увеличилось до 2Dx. В зависимости от этого временной интервал также увеличивался:4X1. 97 = 7,88 Н.

Смотрите также:

• Предмет теплотехника

Подземный кабель	Периодический перенос тепла
Двухмерная стационарная теплопроводность	Теплопроводность при плавлении или затвердевании