Оглавление:




Основное свойство непрерывной функции
- Основные свойства непрерывной функции. С точки зрения здравого смысла, «непрерывная кривая» имеет другую характеристику. Пусть A и B — две точки на графе 9 (x :), координаты x0, φ (* 0), xi 9 (q; -0). Пусть X — прямая y = t). Где 9 (* o) 9 (xi) — утверждение, что граф cp (x 🙂 пересекается с X, Эквивалентно утверждению, что существует значение x 9 (n 🙂 = m] между x0 и xx.
Другими словами, когда x изменяется от x0 до xt, 9 (x) должно получить каждое значение от y0 до y хотя бы один раз. Если φ (π) — непрерывная функция от q, мы фактически обладаем этим свойством в смысле определения §99. Справа от x0 находится определенный интервал для значения x. Фактически, 9 (x <,) и, следовательно, 9 (x) намеренно меньше, чем если бы абсолютное значение y (x) -9 (log) было меньше, чем h.
Поэтому мы заключаем, что непрерывная функция φ (*) требует следующих свойств: А для v0 <- /) <> существует значение x между 9 (a 🙂 = yj между x0 и xx. Людмила Фирмаль
W непрерывен при x = x0, Это условие выполняется, если x достаточно близко к xn. Аналогично, слева от xt находится фиксированный интервал значений x, и в этом случае рp (x)> η |. Разделите все значения x между x0 и x1 на два класса L и R следующим образом: (1) Присвойте все значения переменной x классу L. Таким образом, φ есть л * = $ и все значения х от х0 (2) Для класса R любое другое значение x, т. Е. Φ () <τ) или x0 Тогда ясно, что эти два класса удовлетворяют всем условиям, наложенным на класс Lt Rn в разделе 17, и, таким образом, определяют разделы в вещественной области. £ 0 — это число, соответствующее этому разделу.
Предположим, что £ 0 принадлежит первому В высшем классе φ (0 0) = + k. Тогда IKO ^ 7), поэтому Это противоречит условию непрерывности для jc = E0 для всех значений Γ, меньших £ 0. Если 9 (S0) = -rj-, то I ‘- Вы можете найти любое число больше £ 0, затем любое Между числами, такими как £ 0 и qp (£ «) ^ f). В каждом случае вы можете найти любое близкое число, что соответствующее значение cp (x) отличается более чем на k. (Π) adj; = £ 0. В результате cp (£ 0) = -d) и теорема доказана. Обратите внимание, что мы доказали больше, чем явно указано в теореме.
| Символы, порядок малости и порядок роста | Системы интервалов на прямой. Теорема Гейне — Бореля |
| Непрерывные функции действительного переменного | Колебание непрерывной функции |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Фактически оно оказалось минимальным значением x для φ (η 🙂 = 7). С другой стороны, совершенно не очевидно, что минимум значений x, для которых функция принимает определенное значение, и это, как правило, неправильно. Однако, как мы видели, это относится к непрерывным функциям. Легко видеть, что доказанная обратная теорема неверна. Например, функция, график которой изображен на фиг. Каждое значение между (* 0) и <p (x:,) принимается как минимум один раз и является прерывистым в одно и то же время. И функция <р (х)
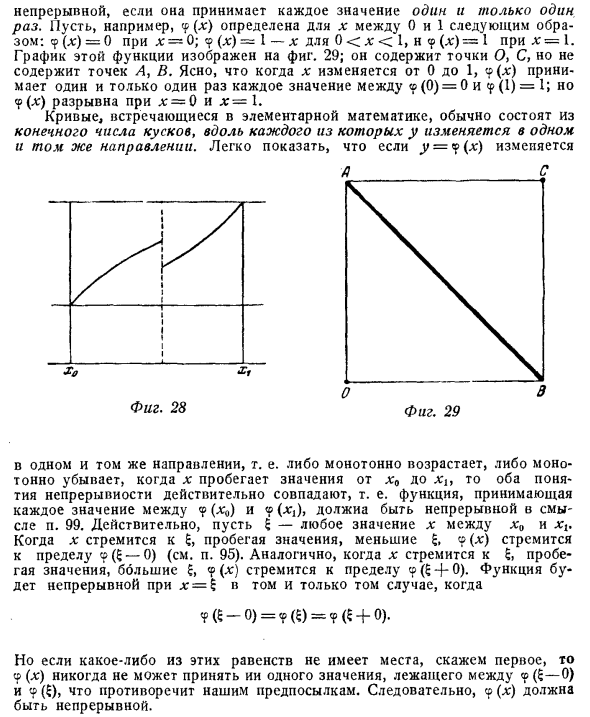
Например, предположим, что вы определяете b (x) для x между 0 и 1 следующим образом: <p () = 0η = 0; (X) = 1-0 ) = 1 прил .: = 1. График этой функции показан на фиг. 29; Включает точки O и C, но не включает точки A и B. Он изменяется от 0 до 1. <p (lg) принимает только одно значение от φ (0) = 0 до <p (1) = I. Однако φ (a) разрывно при x = 0 и x — 1. Кривые, найденные в элементарной математике, обычно состоят из конечного числа частей, причем y изменяется на единицу вдоль каждой Когда x проходит через значения в одном и том же направлении, то есть от x0 до x, он монотонно увеличивается или уменьшается монотонно, и оба понятия непрерывности фактически совпадают, то есть φ (x <,) и φ (*, )
Если каждое значение получено только один раз, оно является непрерывным Людмила Фирмаль
Должен быть последовательным в смысле §99. На самом деле, пусть $ будет значением x между x0 и xt. Если x имеет тенденцию превышать значение, малое o (ar) ограничивается 9 (6-0) (см. §95). Аналогично, если x имеет тенденцию превышать значение, большее 6, (X) стремится к пределу φ (£ + 0). Однако, если какое-либо из этих уравнений не выполняется, например, в первом случае, 9 (n;) не может принимать одно значение между φ (6-0) и 9 ($). Следовательно, φ (a ‘) должно быть непрерывным.
<P «-0) = <p (5) = <p (5 + 0). Однако, если одно из этих уравнений, например, первое, не выполняется, 9 (;;) не может принимать одно значение между «($ -0) и 9 ($). Не согласуется с предположением, поэтому φ (a ‘) должен быть непрерывным.

