Теплообмен при свободном движении жидкости

Теплообмен при свободном движении жидкости

• Теплообмен со свободным движением жидкости Свободное движение или конвективная передача тепла в свободном потоке происходит из-за изменений плотности жидкости из-за нагревания. Свободная конвекция происходит в стенках печного отопления, трубопроводах, батареях центрального отопления, холодильниках охлаждения продукта и так далее. Этот тип теплопередачи играет важную роль

как в промышленности, так и в повседневной жизни. Свободный теплообмен происходит в неравномерно нагретых газах или жидкостях как в ограниченном, так и в бесконечном пространстве. Когда температура тела выше, чем окружающий Chred, слой жидкости, нагретый от тела, становится легче и поднимается из-за создаваемого подъема, и холодный слой выходит из окружающего пространства. Поэтому есть свободное движение. Крупномасштабное

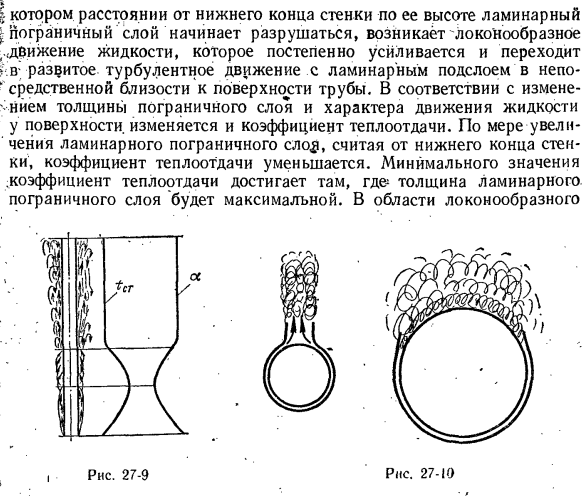
глубокое экспериментальное исследование теплопередачи в свободном потоке выполнено ученым М.В. Кирпичевым, М.А. Дирижируют Михеев и его ученики. Рассмотрите возможность свободного теплообмена в неограниченном пространстве возле вертикальной пластины или трубы. является ламинарным или турбулентным. Характер движения жидкости в основном зависит от температуры напора Дt-tcr- / f. Где / ст —

Результирующее свободное движение жидкости в вертикальной плоскости Людмила Фирмаль

температура нагреваемой поверхности. / f — температура неподвижной жидкости вдали от поверхности. При низких значениях температуры напора по всей поверхности наблюдается ламинарное движение жидкости. При высоких давлениях турбулентный режим движения является доминирующим. Форма тела играет второстепенную роль в развитии свободного движения.

Наиболее важным фактором для свободного движения жидкости является длина поверхности, на которой происходит теплообмен. «Аналитические решения проблемы определения теплообмена при свободном ламинарном и турбулентном движении были реализованы с некоторыми упрощенными допущениями, поэтому эти решения были не очень практичными. Большая работа была проделана по передаче тепла в свободном потоке жидкости с

использованием горизонтальных и вертикальных плюсов, проводов, труб, пластин и шариков. Эксперименты проводились с использованием воздуха, водорода, углекислого газа, воды, масла и различных органических жидкостей. В результате обобщения экспериментальных данных получено эмпирическое уравнение подобия. Чтобы определить средний коэффициент теплопередачи для свободного ламинарного потока вдоль вертикальной стенки, можно

• использовать следующее уравнение: at / st = const ‘* Nuj = 0,63 (Gr / -Pr) 0,25; ‘(27-30) <7CT-Const m) Ht I = 0,75 (Gr, Kl gRG) ° ’25 (PrG / Yst) 0’25. , (27-31) В этих уравнениях температура жидкости вдали от нагретой поверхности считается определенной температурой, а длина поверхности, измеренная от начала теплопередачи, считается определенной величиной. Формула была получена для теплоносителя с числом Прандтля 0,7-3 и 103, 103 1-Prz> 6 • 1010, предлагается

следующее уравнение: *:» •• * ••% ■ N1 ^ = 0,15 (Crz.,; Prz) 0.zz (pr> k / pGst) 0,25 В (27-32) Определенная температура и линейный размер такие же, как в уравнении (27-31). Для 10® 25 (Prz I Prz) ° 25. (27-33) В этой формуле температура капли или газа вдали от трубы используется в качестве температуры измерения, а диаметр трубы используется в качестве размера измерения. Рядом с горизонтально нагретой поверхностью движение жидкости обладает особыми свойствами и зависит от положения и размера пластины (см.

Литературу по этому вопросу). Однако формула (27-33) рекомендуется для приблизительного определения коэффициента теплопередачи в горизонтальной плоскости. теплопередачи, рассчитанный по уравнению (27-33), увеличится на 30%. Когда поверхность обращена вниз, коэффициент теплопередачи уменьшается на 30%. В этих случаях меньшее из пластин считается установленным размером.

Кроме того, если поверхность нагрева обращена вверх, коэффициент Людмила Фирмаль

Теплообмен в ограниченном пространстве со свободным движением жидкости является более сложным процессом, и количественные законы отличаются. Примерные расчеты для наиболее важных случаев описаны в специализированной литературе. Контрольные вопросы и примеры в главе XXVII 1. Какова средняя температура жидкости? 2. Как определяется средняя температура жидкости? 3. Как определяется средняя скорость жидкости? 4. Как определяется эквивалентный диаметр некруглого канала? 5. Может ли поток

жидкости до числа Рейнольдса перейти из режима ламинарного потока в режим турбулентного потока? 6. Как свободная конвекция во время движения ламинарной жидкости влияет на теплообмен? 7. Какое уравнение подобия рекомендуется для ламинарного движения жидкости? , 8. Какое уравнение подобия рекомендуется для турбулентного движения жидкости? 9. Какая разница в теплопередаче в катушке? 10. Какое уравнение подобия

рекомендуется для перемещения жидкости вдоль пластины? 11. Чем отличается однотрубный процесс теплообмена при боковом движении жидкости? — 12. Какое уравнение подобия рекомендуется для одной трубы при боковом движении жидкости? 13. Какой пучок труб используется в технологии? • 14. Объясните подробно характер очистки трубных пучков при боковом движении жидкости. 15. Какое

уравнение подобия рекомендуется для пучка боковых движений жидкости? •% — 16. Как определяется средний коэффициент теплопередачи пучка труб? е 17. Характеристики теплопередачи жидкого металла. 18. Аналогичные уравнения для жидкометаллического теплообмена. LY. Теплообмен на высокой скорости. 20. Какова температура тормоза? 21. Каковы особенности числа Маха? 22. Что? Какая у вас температура? 23. Какова скорость восстановления? 24. Какое уравнение подобия определяет теплопередачу при высоких скоростях жидкости? 25. Пожалуйста,

объясните механизм свободного потока. 26. Объясните характерную картину свободного движения жидкости вблизи вертикальной стенки. 27. Какое уравнение подобия определяет теплопередачу свободного движения жидкости? в Пример 27-1. Определить коэффициент теплопередачи и количество тепла, передаваемого в поток воды в горизонтальной трубе диаметром d = 0,008 м и длиной I-6 м, если скорость w = 0,1 м / с \ температура воды / w = 80 ° C вы.

Температура стенки трубы tCT = 20 ° C At / f = 80 ° C t K (= 0,675 Вт! (М • град), v) K = 0,365 X Х 10 «6 мг / с \ рж 6,32 • 10-4 * (градус Рж = 2,21). • Gst = 293 ° К, Rgst = 7,02. Используйте эти количественные значения, чтобы получить: Re, K> d = wd / v = (0,1 • 0,008 • 106) / 0,365 = 2190; Re «, 3d = 13,2; WG 43 = 1,4; (Pr> k / Prst) ° ’25 = 0; 75. Температура головы / л = / ст = 60 °. Грассхоф число n gd * ¥> AT 9,81 ‘0,0083-6,32’ 10-4-60, .Q 1 HP ‘7- (0,365.U-0) ® — 1-43,10; Grα, ld = 4,12. Используя уравнение (27-6) -N ~ u „<) d == 0,15 Re ° ‘3S • Pr £ £ 43 O ^ (Prz / Prst) 0’25; Nu = 0,15,13, ​​2,1, 4,4, 12,0,75 = 8,56, v a = Nuw „- = 3,56–0,675 ^ y24 Вт / (м * град). Wt <1 д 0,008

Не вводите коррекцию длины трубы, потому что ltd> 50. Количество тепла, передаваемого по всей трубе Q = ndla (t} K- / St) = 3,14 • 0,008. 6 • 724. 60 = 6540 Вт. Пример 27-2. Коэффициент теплопередачи воздуха, протекающего со скоростью w-10 м / с, определяет стенку прямой трубы диаметром d-0,1 м и длиной f = 2 м. Средняя температура / f = 120 ° C. Когда f = 1 20 ° C, Xl = 0,0334 Вт ‘(м • град) \ vw =’ 25,45 x X 10 «6 м2 / с .-! • В этих условиях Rem xl = 1,306 • 10» мУсек. ■■ •, •• В этих

условиях. % Яеж = wdh = (2-0,03-10е) / 1306 = 46000; Re ° = 630; Rgh = 9,52; Rgo. 38 = 2,35; PrCT = 2,2 л; (Prg / Prst) 0,2b ^ (9,52 / 2,21) 0,25 = 1,44. , Подстановка всех величин в уравнении (27-16) дает: Nuw, d = 0,25 Re £. ВРГМ ”(Ргж / Ргст) ° ‘** =. = 0,25,630,2,35,1,44 = 534, Откуда a = NuWid ^ = 534’575 = 10,200 Вт / (м2 градусов). д 0,03 Согласно графику, учитывая угол атаки, 27-3 определяет поправочный коэффициент e ‘= 0,87. Таким образом, , Ад = Yu200 • 0,87 = 8880 Вт / (м2’дег). , Тепло,

передаваемое в трубу, Q = ndlan AT = 3, f4 • 0,03-5 • 8880 • 70 = 292 * 000 em = == 292 квгп. Пример 27-5. Средний коэффициент теплопередачи определяется конвекцией из поперечного потока дымовых газов с составом H20 = 11%. Стенка 8-рядного трубного пучка с CQ2 = 13% и N = 76%. Трубы диаметром d = 60 мм расположены в шахматном порядке. Средняя скорость газа в самой узкой части балки составляет w = 10 м / с ‘. Температура газа перед пучком составляет Tmtl = 1473 ° К, а за пучком Tl> 2 = = 1073 ° К. Угол атаки 50 °. Не учитывайте загрязнение

лучевой трубки. Давление пара внутри трубы составляет 100 бар, а температура поверхности трубы 7СХ = 584 ° К. В то же время для сравнения производится расчет размещения коридора трубного пучка. -. _ • Расчет теплообмена при поперечном обтекании трубы выполняется для третьей линии балки по следующему уравнению: Коридор расположения труб по формуле (27-19): Nu) 11 (d = 0,26 ReO. «PrO-33 (PriK / PrCT) O.». «По шахматному расположению труб — Формула (27-20): Nu, Kd = 0,41 Re» — *, • Pro. «(Прж / Прст) °. ‘\ Диаметр

трубы принимается за определенный размер, а средняя температура жидкости определяется температурой ^ — Tm = 0,5 (7 \ Kfl + Gl> 2) = 1273 ° К- час Tl = 1273SK * v) значение физического параметра K = 174,3 x X 10-6 мсек \} K = • 0,109 Вт / (м • град) \ Prz = 0,58; Rgh = 0,652; Pr ^ sz = 0, 580,33 = 0,835; «(Prg / Prst) 0’26 = 0,892e’26 = 0,97. В этих условиях Rf (d = wd / v = (10-0,06,10 «> / 174,3 = 3450; Reo.65 = 200; = 3450 ° -6 = 133. Для размещения в коридоре трубы подставьте все значения количества в

уравнение (27-19). NuK = 0,26 • 200. 0,835 • 0,97 = 42,1; см. Уравнение (27-20) для размещения на шахматной доске: Nuln = 0,41 • 133 • 0,835-0,97 = 44,2. Коэффициент теплопередачи в третьем ряду решетчатого коридора «.3-NuB ^ = 42,1 ° J ° 9 -76,7 Вт / (м2 град); 0, Обь Для размещения шахматных лучей a = Nu, u — ^ — = 44,2-0,109 = 8Q3 (W). Вт, 3 Вт д 0 06 ‘ Коэффициент теплопередачи для первого ряда обеих балок: acl = 0,6 ак 3 = 76,7 • 0,6 = 46,0 Вт / (м2. Град) \ al1 = 0,6ash, 3 = 80,3 • 0,6 = 48,2 Вт / (м2-град) , Для второй трубы в связке: aK (2 = 0,9 ak s = 0,9. 76,7 = 69,0 Вт / (м2-град); ‘ash.2 = °> 7 <*, «,» = ° «7 • 80,3 = 56,2 Вт / (м3-град.) ). На

той же поверхности ряда средний коэффициент теплопередачи: Для размещения в коридоре 46,0 + 69,0 + 6,76,7 n „2 ак = — • — = 71,9 Вт ((м2-град) \ 8 Для размещения шахматных лучей 48,2 + 56,2 + 6,80,3 -0. „, ^ Серый = —— = 73,4 Вт / (м2-град). 8 При тех же условиях теплопередача в шахматном порядке выше, чем в коридоре, примерно на 3% больше в этой задаче. Пример 27-6. Определяет теплопередачу при естественной конвекции от вертикального оголенного трубопровода

метром d = 120 мм и высотой h = 6 м к воздуху. Температура стенки Tst = 523 ° К, температура Тл = 293 ° К Найти физическую величину при температуре окружающей среды GJ = 293 ° К. • = 0,026 Вт / (м • град); PrWtd = 0,703; Prz / Prst = I; l> l = 15,06 • 10 дюймов mUsek. Грассхоф номер , 0 ГДж <-W _ 63,9,81. 230. C «= Ht’d v2 293-15, Ob2 Grm> d PrG (d = 7,34 • 1012 0,703 = 5,16 • 10 ‘. В этих условиях движение воздуха является турбулентным, и коэффициент теплопередачи определяется из уравнения (27-32). Nu) Ktd = 0,15 (гр. Пр) ^ 3d3о, 15 (5.16.1012) ° 33 = 2320. Следовательно, коэффициент теплопередачи „= NuiK, ^ H (= 2320 0,026 = ωош / (м> _ град) ч ■ -6 Потери тепла из-за трубопровода Q ^ aF (Гст-7 \ к) = 10. 3,14 • 0,12 • 6 230 = 5200 Вт.

Смотрите также:

Решение задач по термодинамике

Теплообмен при поперечном омывании одиночной трубы	Теплообмен при кипении жидкости
Теплообмен жидких металлов	Теплообмен при конденсации пара