Существование и свойства неявной функции

Оглавление:

Существование и свойства неявной функции

Существование и свойства неявных функций. Здесь мы рассматриваем не только существование единственного n e I в функции y=f (x), но и существование последней характеристики непрерывности и Дифференцируемости. Теорема 1. 1) если предположить, что функция P (x, y) определена и непрерывна, то вместе с ее подфункциями Px ‘и Ru’ точка L40 (x0, y0); 2) P (x, y) будет равна нулю в этой точке: p (XY, y o)=O, наоборот, она будет равна 3.） Тогда в некоторой окрестности a)§=(x o-x o-g.UO-uo»B&’)points7I0

(x0,y0)уравнение (1) определяет y как уникальную функцию x: _y=/(x); b) для x=x y эта функция принимает значение y:/(x0)=_u0;C) интервал А) пусть Ru'(x0, z>0)0. Производная от 1) R>эта производная положительна P’u{x, _u)>0 и в достаточно малой окрестности точки (x0, _u0))Возьмем, например, одно неравенство 1Ru (■ * ■. Х) — р ‘ У (0>У О)|<ру (0. У О) — 182Ч. Неявная функция. Функциональные детерминанты z A m K n u t y Y прямоугольник&=K o-3’, x0+V ‘ z u. — x+Y], лежащий полностью в этой окрестности, записанное неравенство выполняется во всех отношениях. Таким образом,сразу следует,что для любой константы x из интервала[XO-o’,

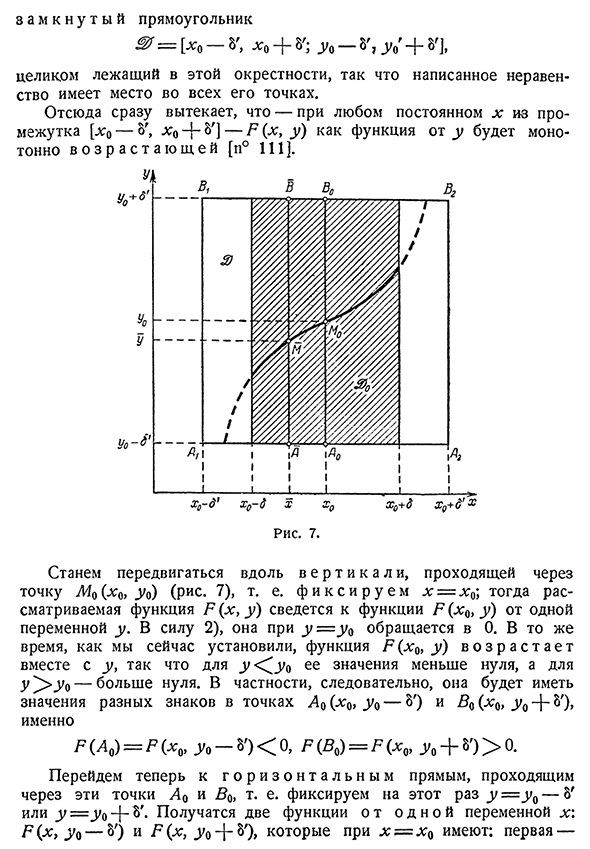
x0+&’]-P(x, y), как функция y, c t a y Sch e y[n°111]. Рис 7. Мы проходим через точки m o Людмила Фирмаль

Ko, _uo и движемся вдоль e R t и l I. 7), t-e-f и K s и R u E m x-x0; рассматриваемая функция P (x, y) сводится от одной переменной y к функции P (x%, y). Благодаря 2), что из y=y B изменяется на 0. В то же время, как мы теперь установили, значение y<^y^^меньше нуля, а в случае y ^ >_u0 больше нуля, отношение o z p A C t A e t вместе с y, в частности, Ko, y (-8′) имеет другое знаковое значение в предыдущей точке, а значение P (Vo)=P (x0, l+8′)>0. Теперь изменим прямую, проходящую через эти точки, на g O R и z o n t a l n s m и исправим y-y y-8’or=_u0-|-8′. P (x, y-8′) и P (x, _uo+8′), который имеет x=x^:

первый-3151§I. неявная функция 183 Отрицательные значения, а вторые-положительные. Однако, поскольку условие 1) эти функции непрерывны), существует окрестность (x0—B, x0-4-y) точки x o (O<^8^8′), и обе функции содержат) z, n*AK, так что x0-8<^x0 & ( * ) Предполагается непрерывность функции P (x, y)относительно множества переменных x, y.**) это следует из N°37, 2), ср. Сноска на стр. 181. П(х, у, Z/о — &’ — <0,р (х, z/0+в’)>0. Другими словами, в нижнем и верхнем основаниях D1D2 и XB%, учитывая, что вдоль отрезков длины 28, точки исходного прямоугольника имеют центры AO и B§. Рассмотрим вертикальный отрезок, соединяющий точку A (x, UY-In’) и s/0+^, фиксируя значение x=x(x0—b,x0) со значением x=x (x,UY-In’) и S /

0+ ^ -вместе с ним наша функция снова возвращает переменную y 0,v () =v (x y z>0 + 8′)>0,тогда из теоремы вольцано-Корси[n-68]. значения y = у, z>0-В а У0 ‘в’, эта функция V (х, г) исчезает: G (x, z/)=0. И здесь, исходя из монотонности функции y^§^y, можно сказать, что (x, 3/) при 5=50, y будет иметь значение y в интервале (y0-z>0 8′), e в e n o e будет иметь E d и n s t. каждый вертикальный отрезок AB имеет только точку M(x, Y), которая обнуляет левую часть уравнения. Следовательно, ОК Р Е С т н ы й=ОО-x0-R8;_u0-8′,z/0 8′)Т О Ч К И Л 40(x0,3/0)у Р А В Н Е Н И Е(1),Д Е Й с Т В и Т Е Л Ь Н О,О П Е Д это,исходя из того, что в(x0, Uo)=0 e, z>0 есть (U0-z’o+y, x=x0 вместе с уравнением (1) 184chap. Неявная функция. Функциональные детерминанты В) переходим к доказательству утверждения С) и г), точно понимаем

неявную функцию y=p (x), которая определяется формулой (1) по y и удовлетворяет ей таким же образом. Увеличенное значение X — (- D x соответствует 4-4U=/(x и уравнение, удовлетворяющее ему (1): P(x&x, y+A_u)=0. Очевидно, что приращение AT7 (x, y)=P (X Ah, y4-D_u)-p (x, y)=0. Здесь мы преобразуем это уравнение, используя формулу конечного приращения[n°102]: 0=P(x4-x&x,y Du) — P(x,_u)==[G(x4~Ah, z / +Du) — P (x, z/Du)]4- А-[Р^У+^ — Р^У)}= =Р ‘х(Х4 — ^х, У4″ Ду• * к Х4-ру(х, У4-61a_u)•A_u(0<6Д<1), Откуда ______Do _7?х(х+0Dh,у+ду) D x-R ‘ y^y+^y)во-первых, давайте убедимся, что Ah->0 имеет a_u->0, то есть функция y-R(x)непрерывна. У нас есть Du, / / M x+e D x, y+Du) / DX ru (x, Y+#Y)

, но непрерывная функция b& / Px ‘ / ограничена сверху конечным числом Людмила Фирмаль

7I[n°137]] 1^-1^м , И в то же время, П О Л О В и т е л ь я непрерывная функция R>, имеющая наименьшее значение/n[n°137], также положительная, ограничена ею снизу: Ру т0. Теперь это легко получить баллы Я делаю свой M|DH I t Или / Г г|^1М Оттуда следует необходимое предложение.316]§1. Неявная функция 185 d) Если вы вернетесь к эквиваленту (3), скажем, x равно 0. Так как мы уже знаем, что одновременно и p’u->0, то рассмотрим непрерывность функций P’X и P’U и тот факт, что P’U0 находится справа от полученного нами предела. Р’х у) Р У(,У)’ Таким будет предел левой части уравнения (3), поэтому существует производная y по x: L (x)=Y^=NT_ _ R’X ( * , Y) ~Р у (, у)’ (4) Если вы назначаете/(x) вместо Y, вы получаете /'() = ^(Х,/(Х ) ) P y (, /()) ‘так как числитель и знаменатель имеют непрерывные

функции и знаменатель не исчезает, то ясно, что/'(x)также является непрерывной функцией. Теорема прекрасно доказана. Таким образом, по характеристикам функции/(x, y), заданным непосредственно нам, мы можем определить характеристики функции _y=/(x), которая не имеет непосредственной работы! Мы уже упоминали в пункте 314 геометрическую интерпретацию вопросов, которые мы здесь изучили. Если кривая задана «неявным» уравнением (1) и ее потоком P\, 0, то в окрестности этой точки кривая может быть представлена»явным»уравнением вида следующего, конечно, x и y могут поменяться ролями: если в какой-то точке в окрестности P’x0 кривая может быть представлена тем же»явным»уравнением только в[210] (как P’x=0, так и p’u=0), то наша теорема не находит применения. 316 Неа

Исторические замечания о перестановке двух предельных операций	Неявная функция от нескольких переменных
Понятие неявной функции от одной переменной.	Определение неявных функций из системы уравнений