Оглавление:


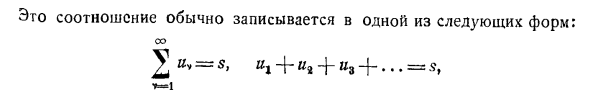

Предел n(х— 1)
- Я Кроме того, с первым неравенством (7). 74 с — ф полож L Следовательно, 1 —> 0. Итак, для «> я»: но Ит! ) = F (α), л-оо Где f (a)> 0. но L л (‘W — 1) — * IV * -1) • Пределом является n (от V до x-1). Положите r = _ в начале неравенства §74 (3). , S = — • Тогда получи. Я если e> 1. Следовательно, если 0 Таким образом, если £ = — <1, то „(UT-1) — / (а). N Наконец, если g = 1, (| / n-1) = 0 для всех значений n. Таким образом, вы получите следующие результаты: llmn (\ fx— ) Определите функцию x для всех положительных значений x. Эта функция f (x) имеет следующие свойства: = — / ()> / (1) = 0 Положительный, если q> 1, и отрицательный, если x <1.
Пример. Докажите, что f (xy) / (x) + f (y). [Используйте соотношение f (xy) = lim / r (\ Gx-1) = лира [n (\ Gx- )} Gu + n (fry-1)}. ) 76. Бесконечные линии. Предположим, что u (x) является функцией от n, определенной для всех значений r. Добавление значения и (v) для v = 1, 2, i, другой функции i, т.е. 5 () = «0) + K (2) + … +» («)> Он также определен для всех значений n. Здесь полезно немного изменить обозначения и написать последнее уравнение на форме. = «! +» * + • ..- Mi. Или, короче говоря, L Но я (] » » -1) — / (а) и (см. Пример XXVII.10) Соотношения обычно записываются в одном из следующих форматов и V = + + +. = Y = 1
Ниже мы видим, что эта функция соответствует натуральному логарифму x. Людмила Фирмаль
Точка также указывает, что последовательность для термина us является бесконечной. Вообще говоря, смысл этих уравнений состоит в том, что сумма возрастающего числа слагаемых в u постепенно уменьшает разность от предела s. Точнее, если указано. Для любого небольшого положительного числа S вы можете найти π0 (8) так, чтобы сумма первых π0 (8) или более высоких членов находилась между 5-8 и s-j-S. я ^ 10 (§). Эти условия называют серией Сходитесь к бесконечному ряду и скажите, что 5 — сумма ряда или сумма всех кленов в ряду.
| Предел | Общие теоремы о бесконечных рядах |
| Несколько алгебраических лемм | Бесконечная геометрическая прогрессия |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Поэтому, когда эти ряды — {- и.2-f -… сходятся, чтобы иметь сумму s, или сходятся к сумме s, или просто сходятся к s, сумма = + + Первые n членов ряда, как правило, ограничены 5 я-ω, поэтому такие соображения бесконечного ряда, за исключением концепций, которые читатель уже знает в первом абзаце этой главы, Нет необходимости вводить новые концепции. На самом деле сумма — это просто функция 9 (n), выраженная особым образом. Функция 9 (i) может быть выражена так: Это значит 9 (i) = 9 (1) + {9 (2) -9 (0} + … + {9 H; Поэтому удобно сказать, что φ (π) сходится к пределу / из π-ω (вместо стремится).
В случае sn— ~ j-oo или sn — * — oo мы говорим, что ряд ui ui ••• разветвляется или lr + oo разветвляется или k-co соответственно. Эти термины могут быть применены к любой функции 9 (ей). Следовательно, если 9 (i) — * — {- ω, то можно сказать, что 9 (i) расходится. Если sn не является конечным пределом, Если ни k — [- co, ни k-co, sn колеблется с границами или неограниченно.
В этом случае говорят, что ряд колеблется с границами или неограниченно 1). Людмила Фирмаль

