Оглавление:





Резонансное рассеяние заряженных частиц
- Резонансное рассеяние заряженных частиц Рассеяние заряженных ядерных частиц (например, Протонный звук), ядра ближнего действия Есть также сила, кулон, который медленно уменьшается Сотрудничество. Теория резонансного рассеяния встроена в это Случаи так же, как описано в § 133. разница Волновая функция Регионы за пределами ядерной энергетической зоны (га).
- Вместо решения уравнений свободного движения (133.2) Точное общее решение кулоновского уравнения Шредингера Поле. Соотношение между 1 / к А длина переменного подвесного устройства = H2 / (r a Z i ^ e 2) (ш Данная масса сталкивающихся частиц произвольна Ним 1). 2 G i 1 1 я 4 г. 4 г. ~ 9, р , sin4 $ cos4 $ sin2 $ cos2 $ (137,9) 1) Теория, объясненная ниже, — Л. Д. Ландау и Я. Разработано А. Смородиным. Ким (1944).
В этом случае скорость частицы все еще предполагается Достаточно маленький, чтобы fc a <1. Людмила Фирмаль
При движении с I = 0 в силовом поле кулоновского поля, уравнение Радиальная функция Уравнение Шредингера% = ri? о X «+ (k 2-1) x = 0 (138,1) (Подвесной блок используется здесь). § 36 нет Учитывая решение этого уравнения, оно следует конечным требованиям х = г для г = 0. Это решение показано здесь. Существует формат через Fq (см. (36.27), (36.28)) F0 = Aeikrk r F ^ + 1,2, -2 ik r), A 2 = (138,2)
Асимптотическая формула этой функции на большом расстоянии Есть Fo «sin kr- ^ ln (2kr) + 5 бочек, 5 бочек = argT ^ l + (138,3) Первый член разложения малых r (kr <1, r <1) F0 = Akr (l + r + …). (138,4) Однако, если вы измените граничные условия, Функция на нуле не важна и обязательна Общее решение уравнения (138.1), которое является линейным Сочетание двух независимых интегралов.
Параметры вырожденной гипергеометрической функции (138.2) выглядит следующим образом (целочисленное значение параметра 7 = 2) Математически случай аналогичен случаю, указанному в конце §d. Добавлен. По инструкции там Получить второй интеграл уравнения (138.1) Функция F в (138.2) с другими линейными комбинациями Согласно (d.14), два члена, чье общее количество вырождено Гипергеометрическая функция.
Такой выбор Сочетая эти терминологические различия, второй независимый form1) (138,1) (представлен Go) G «= 2Im-1-4 ‘-N (Функция Fq является реальной частью стоящего здесь Expression). Асимптотическая форма на большом расстоянии Gq ~ cos (кг- ^ В 2кр + <*> оУЛ ^? (138,6) 1) Функции Fo и Go (и функции, определенные аналогичным образом) Fi и Gi s / f 0) называются нормальным и нерегулярным кулоном соответственно.
Новая функцияПервый член малого расширения r (138,7) Где C = 0,577 … постоянная Эйлера, а h (k) обозначает функцию камыш (Где φ (r) = Γ ‘(z) / Γ (z) — логарифмическая производная функции Γ )) 1). Запишите общий интеграл уравнения (138.1) в виде суммы Где ctg 5o является константой. Эта постоянная спецификация выбрана Следовательно, асимптотическая форма этого решения.
Так что 5 ° — это дополнительный сдвиг фазы волны Функция с ближней мощностью. мы Должен быть связан с постоянной появлением на границе Условие (x ‘/ x) | m — const, рассмотрим замену Волновые функции в области ядерных сил. но С учетом расходимости логарифмических производных (таких как В г) х ‘/ х для г ~ ^ 0, не относитесь к этому условию.
- Ноль, но сколь угодно маленький, но конечный Значение г = р. Расчет (с использованием формул (138.4) и (138.7)) Эквивалентен производной x ′ (p) / x (p) и константе, Форма граничных условий Левая часть уравнения не зависит от k Константа 21п2р + 4 (7; включите их в const и покажите позже Это использует -k.
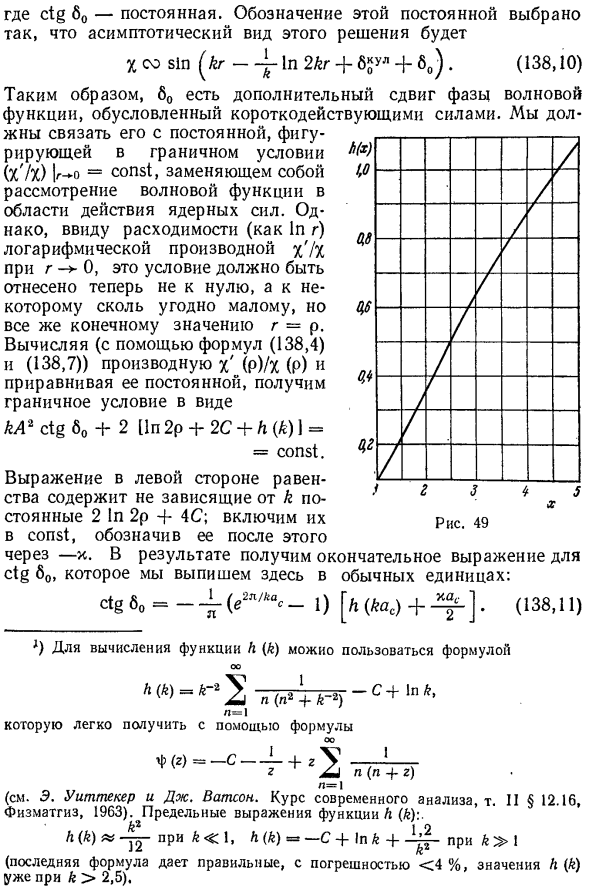
d) Расширение (138.7) взято из (138.5) с использованием расширения (d.17). В этом случае известны отношения (Это легко получить из Γ (z + 1) = zF (z)) и значений φ (1) = -C, φ (2) = = -C + 1. (138,8) X = const i Fo ctg + G0) (138,9) X и грех kr- ^ ln (2kr) + SqYJI + <пл. (138,10) kA2 ctg > 0, то есть при переходе на незаряженную часть Цам, формула (138.11) относится к ctg ^ o-— x / k Матчи (133,6). На рисунке 49 показан график функции h (x) 1).
Результатом является окончательная формула Для ctg ^ cb напишите здесь в нормальных единицах. Людмила Фирмаль
Поэтому в присутствии кулона «Постоянная» взаимодействия Следующее значение: ч (х) 1,0 27rctg (5o, 2, ч ч -z-n ————— n \ cas) = -k. а (е / с-1) АВС> (138.12) о, 8 0.6 0, 4 0.2 / / г / / / / / / / /! / / г / 4, 5 Слово «константа» Потому что отскок представляет к На самом деле, первый период расширения В небольшом количестве стая функций, которые зависят от коротких свойств Исполнимые.
Малый резонанс Энергия соответствует § 133, для необычно малых значений Константа к. Учти это и улучшай Для точности следует также рассмотреть следующий (^ k2) член в разложении Коэффициенты, включая «нормальные» коэффициенты порядка Ранг, т. Е. (138.12), следует заменить на А2) -to o + \ rok2- Как показано, это может быть связано с наличием резонанса.
В § 133 как истинное, так и виртуальное существование 2 секунды Рисунок 49 г) Для вычисления функции h (k) можно использовать следующее уравнение: ~ 1 h (k) = k 2 ^ 2 ^ n (n 2 + k 2) Легко получить с помощью формулы -C + l н / с, z n (nn = 1 V + z) ‘ (См. Э. Уиттакер и Дж. Уотсон. Курс современного анализа. Т.II, §12.16. М. : Физматгиз, 1963).
Ограничивает выражение функции h (k). K2 h (k) & -k «1, если h (k) = -C + In k + для k» 1 к (Последняя формула дает значение h (k) правильно с ошибкой менее 4% Уже к> 2,5). 2) Указывает значение констант рассеяния протонов a = 1 / x o и ro На протонах: а = —7,8 • 10–13, го = 2,8 • 10–13 см (длина кулоновского блока 2Н2 / т re2 = 57,6 • 10-13 см).
Эти значения относятся к парам антипротонов и протонов Параллельное вращение (параллельное вращение, система из двух протонов, Из-за принципа Паули, вы никогда не можете быть в состоянии S).
Дискретное связанное состояние системы. Вы можете посмотреть 1) Уровень правды или виртуальность уровня по-прежнему Постоянный символ k. Полный фазовый сдвиг волновой функции (138.10) равно сумме ^ кул + 5 /. Следовательно, сечение рассеяния о / (C) = ^ J ^ (2 1 + 1) [exp (2i8fyjl + 2i5t) -1] P; (cos6 »). (138,13) 1 1 = 0 Разница в квадратных скобках выражается как exp (2r ^ kul + 2idi) -1 = [exp (2r ^ kul) -1] + + [exp (2r ^ kul) (e2yr-1)]. (138,14)
Кулоновская фаза SfyJ1 вводит тот же размер Вклад во все / амплитуды рассеяния. Этап 5 / связанный Когда сила ближнего расстояния и I f 0 мала (мала) Energy). Следовательно, заменив (138.14) на (138.13) Оставьте скобки для всех членов суммы. Всего этих участников Амплитуда кулоновского рассеяния (135,9) f ™ (0) = lnsin 2 + 2 AND D) ■ (138Л5)
Вторая скобка (138.14) хранится только в члене I = 0. Следовательно, полная амплитуда рассеяния в f (0) = / kul (0) + ^ (e2r6 ° -1) exp (2r <^ ul). (138.16) Второе слагаемое в этой формуле можно назвать амплитудой Ядерное рассеяние. Тем не менее, необходимо подчеркнуть такие вещи Условное разделение: с учетом определения в (138.11)
Существование кулоновского взаимодействия сильно влияет Этот термин совершенно другой Что происходит с той же силой ближнего действия Заряженные частицы. Специально для Кас 0, фаза А Весь второй член (138.16) имеет тенденцию быть экспоненциальным ( exp (-27t / kas)) до нуля, т.е. ядерное рассеяние — это полностью маска Подвеска отталкивания. г) Л. Д. Ландау, Я. См. А. Смородинский // Ж. Э.
Ф. 1944. В. 14. С. 269 В сечении рассеяния обе части амплитуды мешают друг другу. Друг другу: Da sin4 (0/2) — ,, sm4ka. , / 2, .to cos-m sm- + in, sin2 (61/2) \ ka c 2 So) + 4 (fcacy sin d0 (138.17) Здесь мы предполагаем, что сталкивающиеся частицы разные. Для той же частицы амплитуда рассеяния равна До квадратной априорной симметрии Вызывается (см. § 137).
Смотрите также:
| Система волновых функций непрерывного спектра | Упругие столкновения быстрых электронов с атомами |
| Столкновение одинаковых частиц | Рассеяние при спин-орбитальном взаимодействии |

