Оглавление:




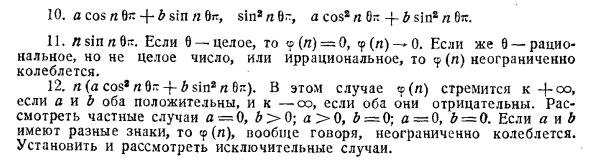

Колеблющиеся функции
- Функция вибрации. Если определение 9 (s) является конечным пределом, k-J-co и k-co оба стремятся к co, cp (l) говорит, что n стремится к co. Функция 9 (l), вероятно, будет колебаться, когда ее значение образует конечное число периодически повторяющихся систем, как в последнем примере. Но конечно
Определение функции вибрации основано на отрицании. Функция вибрирует, если не работает по-другому. Простейшим примером функции колебаний является 9 (л) = (-1) «, Он равен -f-1, если l четно, и -1, если l нечетно. В этом случае значение периодически повторяется. Но посмотрим 9 («) = (-1)» + ±, Его значение -1 + 1,1 + 1, -i + i, i + {, -1 + J …… Ясно, что если l большое, каждое значение приблизительно равно -f-1 или -1, и 9 (l) не является конечным пределом, также. -оо, так поэтому.
Вам не принадлежит это специальное свойство, поскольку оно может колебаться. Людмила Фирмаль
Однако значение не повторяется периодически. В этом случае каждое значение 9 (л) Ниже модуля <P (*) = (-!) «Yo -f-iip Колебание вы. Если l большое, каждое значение почти 100 или -100. Максимальное абсолютное значение составляет 900 (при l = 1). <p (x) = (-1) n, значение -1,2 -3, 4, -5, …. Эта функция вибрирует, потому что нет тенденции к бесконечному пределу, -f-syu, -o. В этом случае, однако, невозможно указать границу, где модуль значения не увеличивается. От разницы между двумя примерами перейдем к следующему определению.
Определение Когда 9 (n), где n имеет тенденцию быть oo, вибрирует, 9 (n) ограничен в зависимости от того, существует ли число K такое, что все значения 9 (n) существуют по модулю Или скажем, чтобы колебаться неограниченно, меньше, чем K, m, то есть 19 (n)] <K для всех значений n. Эти определения и определения содержатся в абзаце. Рисунки 58 и 60 показаны в следующем примере. Пример XXIV. Рассмотрим n вариантов поведения, которые, как правило, используют следующие функции: 1. (-If, 5 + 3 (-1Д10 °% 000 + (-!) «, 1 ООО» (-If -f ™. 2. (-1 ф / г, 1 000 000 Н — л. 3. За 1 000 000-л, (- (1000 000-р).
| Поведение функции от n когда n стремится к бесконечности | Функции от n, монотонно возрастающие вместе с n |
| Определение предела | Другое доказательство теоремы Вейерштрасса |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- i {1 -f (- / *) «} • В этом случае значение > 1 + Vk + 1, поэтому <(я) — * 4- ° Обратите внимание, что в этом случае рp (2A + 1) всегда меньше значения (2k), потому что функция бесконечна и имеет тенденцию к увеличению или уменьшению, но это понятие По нашему определению, она не он. 6. l * {1-b (-1) n}; (-1) ln2 + n; l * + (-1) nl2. 7. грех b ?? Если 0 рационально, но не равно целому числу, уже наблюдалось, что y (n) колеблется в ограниченном диапазоне (например, XXIII.9). В этом последнем случае 0.
Это явно невозможно, потому что 0 является константой и находится между 0 и 1. Если 0 ng — четное целое число, аналогичным образом мы докажем, что cos i колеблется на границе. 8. Когда 0 не является целым числом, невозможно, чтобы sin / r 0- и cosnft- были приблизительно равными для всех больших i, тогда одно из двух значений a и b. (Это можно продемонстрировать с помощью аналогичных рассуждений, но это немного сложнее, чем рассуждения, показанные в примере 7.] 9. sin l 0- -f i, sin l 0- -f-, (-1) n sin n 0 tt.
Таким образом, 0 == kn-kn-, + e „-en -1 = ln + Tln, / „Является целым числом, ^ — • 0. Людмила Фирмаль
10.a cos l 0- 4-b sin n 0n, sin8 l 0t, a cos * n 0- b sin8 l 11. L sin l O *. Если 8 — целое число, л (л) = 0, 0. a> 0, ξ = 0; a = 0, b = 0. Если a и b имеют разные знаки, вообще говоря, cp (l) колеблется бесконечно. Определите и рассмотрите исключительные случаи.Грех. Если 9 имеет разумное значение-л! 0 это <7 Целое число для всех значений l больше или равно q. В результате 9 (n) — * 0. Если 9 нерационально, для его рассмотрения необходимы более сложные вспомогательные инструменты. 14. an- [bn], (-1) n (an- [bn]). 15. Наименьший простой множитель n. Если l простое число, <p (l) = 2, если <f (l) = n′l четно. Следовательно, <p (l) изменяется бесконечно. 16. Наибольший простой фактор р. 17. Количество дней в пятом году н. е.

