Оглавление:


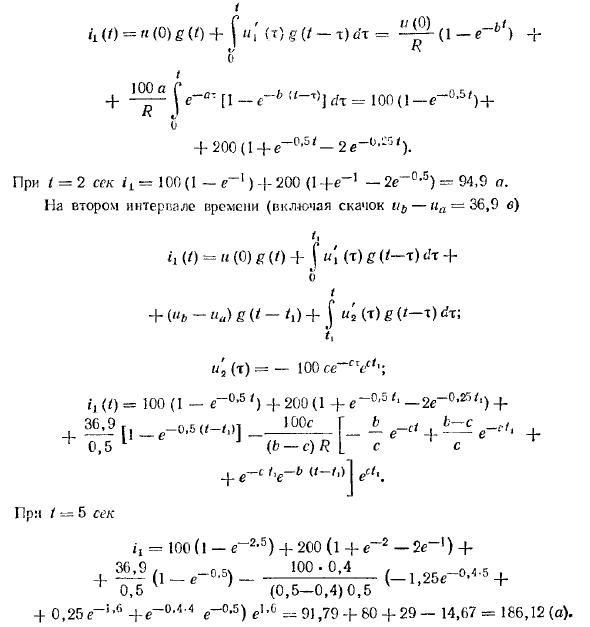

Применение интеграла Дюамеля при сложной форме напряжения
Применение интеграла Дюамеля со сложным напряжением формы. Заставьте напряжение u (r) меняться со временем, но, например, следуйте сложному закону в соответствии с рис. 328 б.
- Начальное напряжение равно n (0). В интервале от m-0 до m = Z2 напряжение плавно увеличивается, и
закон изменения в этом временном интервале равен ux (t). Людмила Фирмаль
В момент m = Zj он внезапно меняется с ua на uht, а затем снова плавно изменяется, но следует закону s2 (m), отличному от первого интервала. Когда m = Z2, напряжение быстро уменьшается от значения до нуля.
Вам нужно найти ток на каждом из трех временных интервалов. Первый интервал означает интервал времени от m = 0 до m = Zj (скачок напряжения от ui до nL не включен).
- Второй интервал от tx до Z2, который включает в себя переходы от un, но не включает переходы от e до нуля. Третий интервал для m> Z2 и включает скачки с нуля.
Продолжите интеграцию по t и в определенный момент поймете, когда вам нужно найти ток. Ток / ток в любой момент определяется действием всех напряжений, активированных до момента Л начального интервала / Г (/) = «(0) g (0 Вт g (t-т) dx (■ 2-й интервал i (Z) = u (0) g (0 4-j «/ (t) g (tt) dx 4- (b-ua) g — I-От + J» 2 ‘ W g (/ -T) t / t.
Термин («* -G) обусловлен скачком напряжения Людмила Фирмаль
от ua к u в момент времени третьего интервала / g.» (0 = U (0) g (0 4-j и / (g) g (t-r) dx 4 — («6-а») gkt-t ^ -r CC + Ju2 ‘(r) g (/ -m) dx 4- ( 0-t) g (t- / 2)
Пример 149. В электрической цепи на рисунке 328 переключатель замыкается в этой точке, и напряжение и (1) изменяются в соответствии с рисунком 328.6; m (0) = 50 дюймов. в первый временной интервал от t = 0 до / 4 секунд, uk (t) -150-100 e ~ at, где a = * 0,25 sel1.
Второй временной интервал от 11a / => 4 секунд = / ,, = 6 секунд a (f) = 50 50-г100 e ~ s, где c = 0,4 секунды ~ 1. Параметры схемы на рисунке 328: / ^ == 0 Lk = »1 gn (вторичная цепь разомкнута), найти закон изменения тока по времени в обоих временных интервалах и значение тока в / = 2 секунды и / = 5 секунд.
Решение I (0 = «7Γ (1- & = — = 0,5 сект»). В первом интервале er. (X) -1G0 и h (f) = «(0) g (0 + fU) g ( / -t) Λ = (1-et ‘) z zA около 100 (1-е до 0,5’) 4-b 200 (1 4-2 e «0’25 ‘) ./ = 2 с 100 (1-c ”1) — | -200 (l -fe» 1-2e «0’5) = 94,9 a.
Па второго временного интервала (включая скачок и? -, Hrt = 36,9 b) ((/) (( 0) ((/) + J «1 (м) г (/ -м) 4 4-0 / + (« »-« J s U-)) + [», CO g 1) L; r, s ‘ (T) = -100 aG «/ ‘1; r, (t) = 100 (1-e-0,5’) 4-200 (1 4-e до 0, s ‘■ -ge-0-25’-) 4-4_ [I е-0.5 (/ — /,)] _, 00 сГ ± ed, -н, +0,5 1 Дж (мс) R [с + s 6 + 4-е до с, ‘е до б до 0) |
ee <|. Prm / -5 л? l * ij = 100 (т. е. «2,5») 4–200 (1–4–2–2e ») 4–1 36,9 /] —os \ 100 ■ 0,4 (–1, 25e— ° ‘4’5 4- 0,5 ‘C} (0,5-0,4) 0,5 4-0,25 е-5’6 4-е «0’4-4 е» 0’5) eh0 = 91,79 4-80 4-29-14,67 = 186,12 (а)
Смотрите также:
| Интеграл Дюамеля. | Сравнение различных методов расчета переходных процессов. |
| Последовательность расчета при помощи интеграла Дюамеля. | Простейшее электрическое дифференцирующее устройство. |

