Оглавление:







Классификация молекулярных колебаний
- Классификация молекулярных колебаний Предварительная теория применяется к многоатомным молекулам Скорее всего, решить проблему электронной классификации смолы MOV, уровень энергии данного расположения ядер. Они Классификация по неприводимому точечному представлению Симметричные группы, принадлежащие рассматриваемому конфу Зарождение.
- Однако в этом случае необходимо подчеркнуть очевидное. Тот факт, что полученные таким образом классификации связаны между собой В этом конкретном расположении ядер, Когда они смещены, вообще говоря, симметрия конфигурации Это рухнуло. Это обычно правильное место Положение ядерного равновесия. В этом случае классификация Даже небольшая ядерная вибрация должна иметь особое значение.
Но, конечно, это не имеет смысла, если вы не можете учитывать вибрацию Как мало. Людмила Фирмаль
С двухатомными молекулами этой проблемы не возникало. Конечно, из-за его осевой симметрии, Ся, с ядерным движением. Есть похожая ситуация Место для трехатомных молекул. Всегда найди 3 ядра В одной плоскости плоскость симметрии молекулы LY. Поэтому классификация электронных терминов является трехатомной Молекулы на этой плоскости (симметрия или Волновых функций по отношению к отражению воды Самолет) всегда возможно.
В нормальных электронных терминах, многоатомные родинки Круто, согласно этому есть эмпирическое правило Большинство молекул с нормальными волновыми функциями Электронное состояние имеет полную симметрию ( В двухатомных молекулах это правило уже упоминалось в § 78). PhD Другими словами, он неизменен по отношению ко всем элементам.
Относится к симметричной группе молекул, то есть единице Неприводимое представление группы. Применение методов теории групп особенно важно Молекулярно-вибрационные исследования (Э. Вигнер, 1930). Требуется квантово-механическое исследование этой проблемы Предлагаю чисто классический вид вибрации Молекулы, с которыми взаимодействует определенное количество систем Частица (ядро).
Система N cha, как известно из механики (см. I, §23, 24) ститы (не по одной прямой) 3Н — 6 КО Легкая степень свободы, из 3N градусов 3 свободы соответствуют переводу и 3 ротации Непрерывное движение всей системы 1). Системная энергия Может писать маленькие вибрирующие частицы Следующим образом: Е = — ^ ^ тарщик + — ^ ^ (100,1) я, я, я.
Где rriik и kik являются постоянными коэффициентами, а u является компонентом Вектор смещения частиц из положения равновесия ( Палубы g, k нумеруют как векторные компоненты, так и числа Частицы). Соответствующее линейное преобразование Ранг u можно исключить из координат, соответствующих (100.1) Для перевода и ротации системы Выберите координаты, чтобы оба были квадратами (100.1) десятичный формат изменен на сумму квадратов.
Нормализуйте эти координаты, чтобы инвертировать все коэффициенты. Entei в представлении кинетической энергии на единицу, получим Форма вибрации энергии E = \ E ■ Qli + \ E ‘»>» E’ Qli- (100-2) г,%% Координаты вибрации Цая называются нормальными. IoA-соответствующая независимая частота колебаний. Некоторые нормальные координаты Та же частота соответствует (для этого Несколько);
Нормальный индекс координат Частота номера и индекс r = 1,2. , , , /, И номер регулировки Относится к той же частоте (/ a-кратность Frequency). Формула молекулярной энергии (100.2) Вариант симметричного преобразования. Это Для всех преобразований, связанных с точками Группа симметрии молекулы, стандартные координаты Qai, r = 1, 2. , , , / A (каждый данные a) преобразуется в линейный г).
Если все частицы находятся на одной линии, количество осцилляторов 3 N-5 степеней свободы (в этом случае вращение Разговор о вращении линейной молекулы, потому что это всего лишь две координаты Там нет смысла вокруг этой оси). Так как они общаются друг с другом, сумма квадратов Это не изменится.
- То есть нормальная настройка Вы связаны с определенной естественной частотой Выполните любую неприводимую, любую молекулу. Установить группу симметрии. Кратность частоты определяется Размерность выражения. Неснижаемый это то же самое Соображения для решений §96 Уравнение Шредингера. Соответствующая частота Два разных неприводимых выражения Случайно.
В этом случае вы должны сделать это снова Отказ от ответственности: Физические нормальные координаты Суть в реальном количестве, Далее два комплексных сопряженных представления соответствуют Одна собственная частота в два раза больше. Часть естественной вибрации молекул Решить сложную проблему конкретного определения нормального Координаты.
Эти соображения позволяют классифицировать. Людмила Фирмаль
Для этого сначала нужно найти (обсуждается ниже Способ) Производительность, сразу же реализованная всеми Координировать (говорить о нем как пол Вибрационная презентация) Эта презентация Разобрать Димо и его на неприводимые части. Определяет множественность собственной частоты и свойства симметрии 3 соответствующих вибрации.
Может получиться Такое же неприводимое выражение выходит на пол Несколько раз, это означает, что нет Несколько разных частот одинаковой кратности с вибрацией Та же симметрия. Чтобы найти полное представление вибрации Мы исходим из того факта, что буквы выражения являются неизменными Относительно линейного преобразования базисных функций.
Так может использоваться как функция для их расчета Основа не нормальная координата, а просто компонент U вектор смещения ядер из положения равновесия. Во-первых, при расчете персонажа, Единственный элемент облака точек G, (Точнее — его положение равновесия) Используйте это симметричное преобразование, чтобы остаться на месте.
День конечно, если под рассмотренным поворотом или размышлением NII G, Core 1 перешел на новую должность, ранее Если было еще одно то же ядро 2, это значит Смещение ядра 1 радиоприемника G переводится как смещение ядра 2. Другими словами, соответствующее ядро (т.е. В любом случае строки матрицы G ^ Диагональный элемент.
Компоненты одного и того же вектора смещения сердечника, Положение равновесия не зависит от операции G. Потому что они обращены только друг к другу, Посмотрите независимо от вектора смещения оставшихся ядер. Сначала рассмотрим вращение C (cf) на угол cp. Вторая ось симметрии.
Пусть они будут ui, uz компонент вектора Смещение конкретного ядра в верхнее положение равновесия Поскольку он движется по самой оси, он не подвержен вращению. При вращении эти компоненты не только преобразуются, У вас есть формула (ось 2 Совпадает с осью симметрии) v! x = их cos (p + uy sin <£, уфу = — укс син ip + уй cos ip, uz = uz.
Характер, сумма диагональных членов матрицы преобразования 1 + 2 cos (p. Если все находится на этой оси Тем не менее, для ядра N c, общий характер N c (l + 2 cos i p). (100,3) Тем не менее, этот символ совместим со всеми преобразованиями 3N Поэтому необходимо отделить соответствующие части Поступательное движение и формирование поступательного движения go) Вся молекула.
Поступательное движение определяется Вектор смещения U центра инерции молекулы. По словам Следовательно, действительная часть символа равна 1 + 2, потому что ср. по Ворота всей молекулы определяются вектором угла Sfl Вращение 1). Вектор Sfl является осевым вектором. Но относительно Вектор оси затвора системы координат работает следующим образом То же, что и полюсный вектор.
Следовательно, вектор Sfl равен 1 + 2 cos (p. Всего, поэтому мы Вам нужно вычесть значение 2 (1 + 2cos ^) из (100.3). так Сразу найти букву х (G) для вращения C ( Полная вибрационная производительность: X (C) = (Nc-2) (1 + 2 cos ^). (100,4) Природа единичного элемента Е, очевидно, только пол Количество степеней свободы вибрации: x {U — 6 (Если N c = N, cp = 0, оно также берется из (100.4)). х)
Насколько известно, малые углы поворота можно рассматривать как века Тора (Ш, абсолютное значение, равное углу поворота, ориентация Вдоль оси вращения в направлении, определяемом законом винта. Opure Следовательно, вектор расщепления 5 (1 явно аксиальный. Аналогично рассчитайте свойства зеркала Преобразование компании S (cp) (поворот угла cp вокруг оси 2) И отражение в плоскости ху).
В этом преобразовании вектор Конвертировать по формуле ux = cos cp + uy sin ip, ufy = —ux sin (p + uy cos cp, u’z = -u z, Соответствует символу, равному (-1 + 2cos ^). так Характер представления, выполняемого всеми смещениями 3N mi u невероятно похож на n h _. N s (-1 + 2 cos (p), (100,5) N s — операция S ((p) (это Число, очевидно, будет либо 0, либо 1.) вектор ru L центр инерции соответствует характеру (-1 + 2 cos cp). Вектор <W — осевое направление.
Он не изменяется при инвертировании вектора или системы координат. С другой стороны, преобразование вращения зеркала S (cp) Может быть представлен как S (<p) = C (cp) ah = C (<p) C2I = C (tr + <p) 1 То есть как вращение угла r + cp, так и последующая инверсия. Следовательно, характер преобразования S ((p) относится к вектору p <W, равный характеру примененного преобразования C (tr + cp)
Нормальный вектор, т.е. 1 + 2 cos (равен 7r + (p) = 1-2 cos, ср. Сумма) Поскольку ma (−1 + 2 cos (y9) + (1–2 coscp) = 0, результат достигнут. Татуировка или выражение (100,5) прямо равно тому, что вы хотите Преобразование вращения зеркала S буква x (S) ((p) в Полная вибрационная производительность: X (S) = Ns (-1 + 2 cos ip). (100,6) В частности, характер отражения на плоскости (cp = 0) x (cr) = Nv, а обратный символ (cp = mr) равен% (f) = -3Nj.
Как только персонаж решен, завершите осциллятор Презентация остается только разобрать Десятичное представление выполняется по формуле (94.16) Используйте таблицу символов, описанную в § 95 ( К этому пункту). Нет необходимости классифицировать колебания линейных молекул Необходимость полагаться на теорию групп. Общий генератор Степень свободы 3N-5.
В вибрации необходимо следующее. Противодействовать атомам, которые остаются в прямой линии 1) так что это не сделано. Количество степеней свободы Если движение N частиц по прямой равно N, то одна из них Соответствует поступательному движению молекул Логотип. Следовательно, число нормальных координат вибрации Атом на прямой является N-1.
Они соответствуют Как правило, N-1 отличается естественными частотами. Остальное (3N-5) — (N-1) = 2N-4, включая стандартные координаты Для колебаний, которые нарушают прямолинейность молекулы. Для них N-2 совместим с двумя разными двойными частотами (каждая Частота Две одинаковые вибрации, перпендикулярные друг другу Самолет) 2). Z a z h 1.
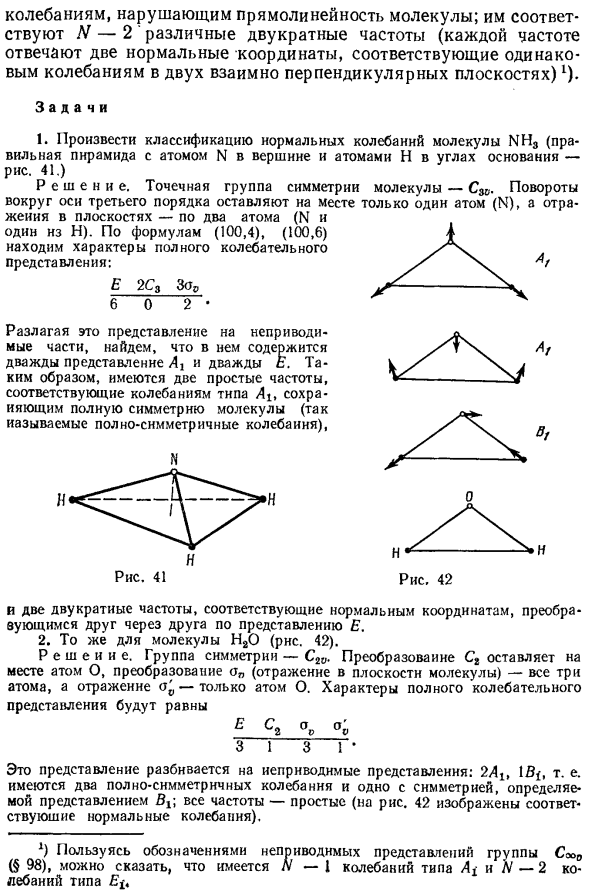
Классифицировать нормальные колебания молекул NH 2 (Нормальная пирамида с атомом N на вершине и атомом H в нижнем углу (Рисунок 41.) Облако симметричных точек определяющей молекулы — СЗУ. Превратите Только один атом (N) остается вокруг третичной оси. И отражение на плоскости — два атома каждый (N и 1 Из Н).
Найти персонажа по формуле (100.4), (100.6) N хвост с полным выражением вибрации: E 2S3 3crv Развернуть это выражение до неприводимого .gis. 4 Вы можете видеть, что первое и второе включены Установите A \ и E дважды. Таким образом, Две простые частоты, соответствующие вибрации типа A i Полная симметрия молекул (так называемая идеальная симметрия) баны), и две двойные частоты, соответствующие нормальным координатам.
Они конвертируются друг в друга по выражениям нац и е. 2. То же самое относится и к молекуле H2O (рис. 42). Рисунок 42 Решающая группа симметрии — C 2v C 2 трансформационный лист Предопределенный атом O, конверсия crv (отражение на молекулярной плоскости) — Все три атома, а отражение cf ‘- это только О. Строгое подчинение будет равным E C2 & V & V 3 1 3 1 1)
Отображается, если молекула симметрична относительно своего центра Вибрация имеет еще одну дополнительную характеристику. Смотрите задачу 10 в этом параграфе. 2) Используйте неприводимое представление группы CooV (§98), вы можете сказать, что существует вибрация N-1 типа A \ n iV-2. E Enter . Это представление делится на неприводимые представления: 2A \, 1B \.
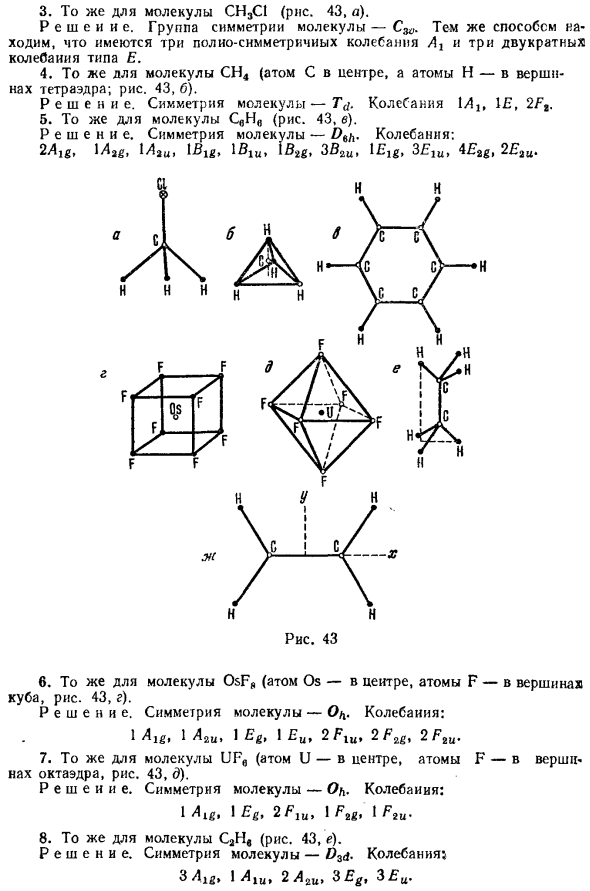
Другими словами, есть две совершенно симметричные вибрации и одна симметричная вибрация, Все частоты определяются представлением (рисунок 42) Соответствующая нормальная вибрация отображается). 3. То же самое относится и к молекулам CH 3 Cl (рис. 43а). Группа симметрии определяющей молекулы — C 3 W.
Таким же образом Вы можете видеть, что есть три совершенно симметричные колебания A i и три двойных колебания Тип Е. Вибрация н н н н F f F / Мистер Мале о , / F. Рисунок 43 4. То же самое для молекулы CGC (центральный атом C, верхний атом H Тетраэдр; Рисунок 43 5). Определить молекулярную симметрию -Тd-вибрации 1А \, IE, 2F2. 5.
То же самое относится и к молекуле SbNb (рис. 43в). Определение молекулярной симметрии — D qh — Вибрация: 2A lg, lA2g, 1A2u, lBig, lBiu, 1B2g, 3B2u, lEig, 3Elu, 4E2g, 2E2u. 6. То же самое для молекул OsFs (атом Os находится в центре, атом F находится в вершине) Куб, рисунок 43 г). Определение симметрии молекулы по вибрации: 1Aig, 1А2и, 1Ее, 1Еи, 2Fiu, 2F2g, 2F2u.
То же самое относится и к молекуле Т U F 6 (атом U находится в центре, а атом F — в вершине) Октаэдр, рисунок 43 (9). 488 M N O G T ATO M N Y E M O L EK U L S CH XIII Определить молекулярную симметрию при вибрации: 1 мкг, 1 Эг, 2Фиу, 1Ф2г, 1Ф2у. 8. е для молекулы C2Hb (рис. 43e). Определяем молекулярную симметрию-Dsd-вибрации: SAlg, l A lu, 2 A 2u, SE g, S E u. 9.
То же самое верно для молекулы C 2 H4 (рис. 43 e / s; все атомы находятся в одной плоскости). Определить молекулярную симметрию -D 2ч • колебания: 3 ^ 4ig, lA-iu, 2 Big, 2Вз, и l £> 2g, 2.8 8 2 ^ (Оси координат выбраны, как показано на рисунке). 10. То же самое для линейных молекул с симметричными атомами азота В середине. Рассматривается ли классификация вибрации решения в тексте?
Нелинейные молекулы участвуют в классификации в соответствии с относительным поведением Однако разворот является центральным. Необходимо различать, является ли N четным или нечетным. Если N четное число (N = 2 p), в центре молекулы нет атома. дать р Половина молекул имеет независимые смещения по прямой р для других атомов — равные и противоположные смещения, р Вибрации, которые оставляют атомы на прямой линии.
Центр и отдых (2 р-1) -р = р-один вибрации этого типа анти-шим Метрика о центре. Кроме того, атом p имеет 2 степени свободы p Для движений, где атомы не удерживаются по прямой линии. Дай сим Равные и противоположные смещения атомно расположенных атомов, 2 р симметричная вибрация получается.
Однако этот номер Нарисуйте две молекулы, соответствующие вращению. так p-1 кратная частота колебаний, удаляя прямо симметричные атомы Слишком много е ((2 р-2) — (р-1) = р-1) — Антисимметричный. Используйте неприводимые обозначения Можно сказать, что существует вибрация группы D ^ h (см. §98 конец), р По (р-1) вибрации типа A \ g и типа A \ u, Eig, E \ u. Аналогичные соображения даются, когда N нечетно (N = 2 p + 1). Вибрация типа p: вибрация A \ g, A ± u, E ± u и (p-1) типа E \ g.
Смотрите также:
| Непрерывные группы | Колебательные уровни энергии |
| Двузначные представления конечных точечных групп | Устойчивость симметричных конфигураций молекулы |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

