Точечные группы

Точечные группы

• Точка группы Преобразование, которое является частью группы симметрии тела Конечный размер (особенно молекула) Так что хотя бы одна точка на теле остается нестабильной Его можно переместить при применении одного из этих преобразований. PhD Другими словами, все оси и плоскости симметрии молекулы Существует по крайней мере одно общее пересечение.

• акт На самом деле непрерывное вращение тела вокруг двух, которые не пересекаются. Отражение на осях сожаления или непересекающихся плоскостях Это приводит к поступательному движению тела. Видимо, вы не можете объединить это с собой. Сим группа Терии с этим свойством называются точками В группах. Прежде чем приступить к созданию возможных типов, Группа представляет простой геометрический метод. Легко распределить элементы группы по Класс.

O a — некоторая ось, а элемент A — Поверните определенный угол вокруг этой оси. Людмила Фирмаль

Кроме того, G Существует преобразование (вращение или отражение) из той же группы. Это относится к самой оси Oa и преобразуется следующим образом Layout. Тогда это показывает, что элемент B = GAG ~ 1 Вращаться вокруг оси О3 под тем же углом, что и элемент Тогда обойдите ИЛИ. Конечно, пожалуйста, подумайте Конвертация ОГ Оси GAG-1. преобразование G -1 является противоположностью G и преобразует ось O в положение Oa.

Следующий ход А оставляет ее в этом положении. в конце концов G возвращается в исходное положение. Вот так B вращается, поскольку ось b остается на месте в результате Вокруг этой оси. А и В относятся к одному классу Следовательно, порядок этих элементов одинаков. Это означает, что они Поворот под тем же углом. Таким образом, результат 2 поворота достигнут.

Если числа совпадают, они принадлежат одному и тому же классу под тем же углом Элементы группы имеют преобразования Одна ось вращения может быть объединена с другой осью вращения. Именно так Точно так же два разных отражения Самолеты принадлежат к тому же классу, если таковые имеются Групповое развитие переводит один самолет в другой. О нас 442 Т Е Р И Й С И М М ЭТРИ И ГЛ. XII Ось или плоскость симметрии, направление Говорят, эквивалентно сочетаться друг с другом.

Требуются некоторые дополнительные комментарии Чай, когда оба поворота делаются примерно одинаково Ось. Элемент, противоположный вращению Ck (k = 1, 2, …, n-1) Круг оси симметрии n-го порядка является элементом C ~ k = C ™ ~ k. То есть вращаться в том же направлении на угол (n — k) (2 тг / н), или Это то же самое, поворачивая 2kt / pv в противоположном направлении.

если При групповом преобразовании происходит поворот на угол Круг, перпендикулярный оси (это вращение меняет направление) Противоположная ось), то по доку Согласно общим правилам чередование Ck и C ~ Один класс. Отражение на плоскости, перпендикулярной Ось и направление также меняются местами. Тем не менее, Имейте в виду, что отражения также меняют направление вращения.

Следовательно, существование не сопрягает элементы Ck и C ~ k Отражение σ ^ на плоскости, проходящей через ось Измените направление оси, но измените направление вращения. C ~ k = crvCk (jv при наличии такой плоскости Симметрии Ck и C ~ k принадлежат одному классу. Когда скручены Вокруг оси под тем же углом в противоположном направлении Сопряженная, то ось называется обеими сторонами.

Во многих случаях легче определить классы точечной группы. Следующее правило. G не группа, Держать инверсию /, и C {группа из двух элементов: I и E. Далее, прямым произведением G x Ci является группа, содержащая: Содержит вдвое больше элементов, чем G, половина из них соответствует Имеет элементы группы G, остальное умножение Я ем последний.

Потому что я коммутирую с другими людьми Преобразование облака точек, группа G x Ci Включает в себя в два раза больше классов, чем G. Каждая группа класса А Число G соответствует двум классам A и A I в группе G x Cj. В В частности, инверсия I всегда составляет сам класс. Затем перейдите к списку всех возможных точек Группа. Начни с самого простого и добавь Добавьте новые симметричные элементы к ним.

Точка группы Подходящие жирные латинские буквы Индекс. I. G r u p p a S p Самый простой тип симметрии включает только одну ось симуляции. n метрика Есть группа из группы C n витков ось n Эта группа явно периодическая. каждый Из n элементов они сами образуют класс. Группа С \ Включает только идентичные преобразования Ему не хватает симметрии.

II. Группа S2n Это группа вращений вокруг оси вращения зеркала. Заказ 2р. Содержит 2n элементов, Видимо периодический. В частности, группа S 2 включает в себя все. Перейти к двум элементам E и /. Также указано C {. знак И если порядок группы является числом вида 2n = = 4 ^ 9 + 2, в этом элементе есть инверсия. по-видимому что (5,4p + 2) 2p + 1 = CW / i = 1- Прямые товары: £ 4 ^ + 2 = С2р + \ x См.

Обозначено Также через C 2p + i, iIII. Группа Cnh Эта группа получается присоединением к pth Порядок плоскости симметрии, перпендикулярной ей. организация na C nh содержит 2n элементов. N витков группы C n и n Зеркальное преобразование вращения C ^ a ^ (k = 1, 2, 3, …, n) (Включая отражение C ^ a ^ = a ^). все элементы ком мутативная, т. е. абелева группа, число классов равно числу элей Милиционер.

Если n четное (n = 2p), группа включает в себя центр Метрика (потому что C2pd = C2an = /). Простейшая группа C \ h Е и А содержат только два элемента Рез Cs. Внутривенно Группа C nv При присоединении к оси симметрии n-го порядка Автоматически после прохождения через плоскость симметрии Похоже, другая (n-1) плоскость пересекается Друг друга вдоль оси под углом 7 г / н (это следует непосредственно Из геометрической теоремы (91.7) 1)).

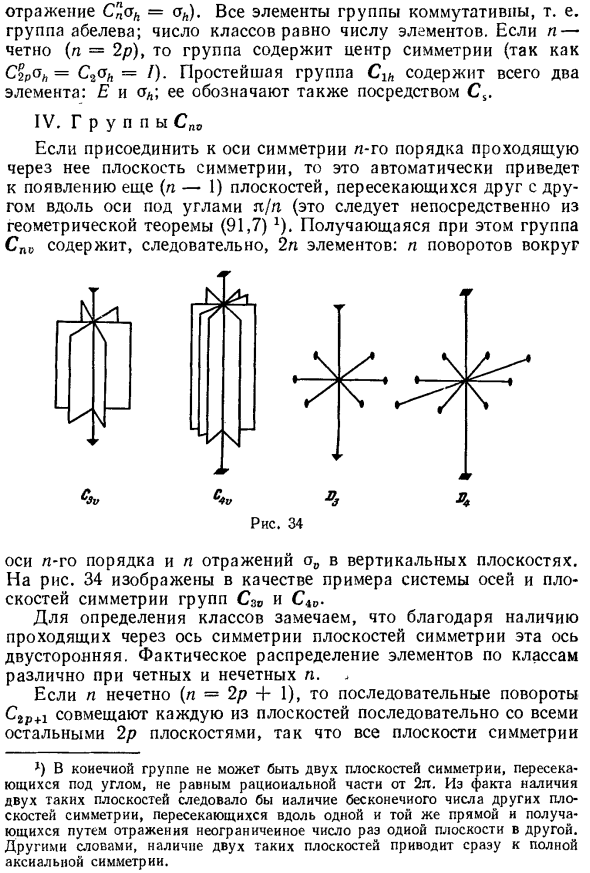
• В результате Таким образом, группа C nv содержит 2n элементов. N Вращение вокруг n-й оси и вертикальное отражение Стальной самолет. 34 показан в качестве примера. Оси и плоские системы систем симметрии в группах C% v и C4V. Определить класс Проходит через ось симметрии плоскости симметрии этой оси х) В конечной группе не может быть двух симметричных плоскостей, пересечений Под углом не равным рациональному числу 27г.

Из факта наличия После этих двух планов существует бесконечное количество других планов. Симметричные плоскости, которые пересекаются по одной прямой Неограниченное количество самолетов, излучаемых отражением Еще один. Другими словами, существование двух таких плоскостей непосредственно связано Для завершения осесимметричный. Между двух стран.

Фактическое распределение элементов по классам. Людмила Фирмаль

Это отличается для четного n и нечетного n. Szu S4 -U Рисунок 34 Если n нечетно (n = 2p + 1), то последовательно Предприятие C * 2p + i присоединяется к каждой последующей плоскости Но во всех остальных плоскостях 2р все плоско Симметрия эквивалентна, и их отражения включены в один Класс.

Во вращении вокруг оси происходит операция 2p. Отличается от парных идентичностей hom, каждый из которых образует два элемента p-класса (C ^ + i и C ^ _ 1? k = 1 2, .. , P); кроме того, E представляет собой другой другой класс. Поэтому только р + 2 класс. Если n четное (n = 2p), непрерывное вращение C2P можно комбинировать попеременно только через один Самолет, две соседние плоскости не могут быть выровнены Друг другу Таким образом, есть два набора, соответствующих р.

Плоскость ленты и, следовательно, два класса p элементов (Отражение) каждый. Для вращения вокруг оси, = E и C% p = C2 каждый составляет класс сам по себе Оставшиеся 2p — 2 хода являются парными, давая еще один p ​​-1 Двухэлементные классы. Все группы C 2P, V являются следователями Но р + 3 класс. V. Группа Д н Когда перпендикуляр прикреплен к n-й оси симметрии.

Вторичная ось, это приводит к Существует еще один (n -1) на той же оси, и, следовательно, всего n по горизонтали Вторичные оси, которые пересекаются под углом м / н. пол Ростовая группа D n содержит 2n элементов. n вращений под углом 7 ° вокруг круга и горизонта n-й оси Согласитесь указать последний в общей оси (C / 2, остальные Вив обозначение С2 для поворота на угол tg вокруг вертикальной линии Ось). Рисунок 34 показан в качестве примера системы координат Группы Z> 3 и Z> 4.

Совершенно похоже на предыдущий случай, но мы уверены, n-я ось с обеих сторон, горизонтальная Если n нечетно, все вторичные оси эквивалентны. или Если n четное, оно образует два неравных множества. Suredoba В частности, группа D 2p имеет следующие p + 3 класса: E, 2 класса Каждый р-ход U2, ход C2 и (p-1) класс 2 поворота вокруг вертикальной оси. Группа D 2P + я p + 2 класс: E, 2p + 1 ход U2, p класс 2 хода Вокруг вертикальной оси.

Важным частным случаем является группа Z> 2. Система Ось состоит из трех взаимно перпендикулярных осей ВТО Роговой порядок. Эта группа также обозначена буквой V. VI. Группа Д нх При добавлении в систему координат группы D горизонталь Плоскость симметрии через вторичную ось n ка, то автоматически отображаются n вертикальных плоскостей Каждая кость проходит через вертикальную ось Одна из горизонтальных осей.

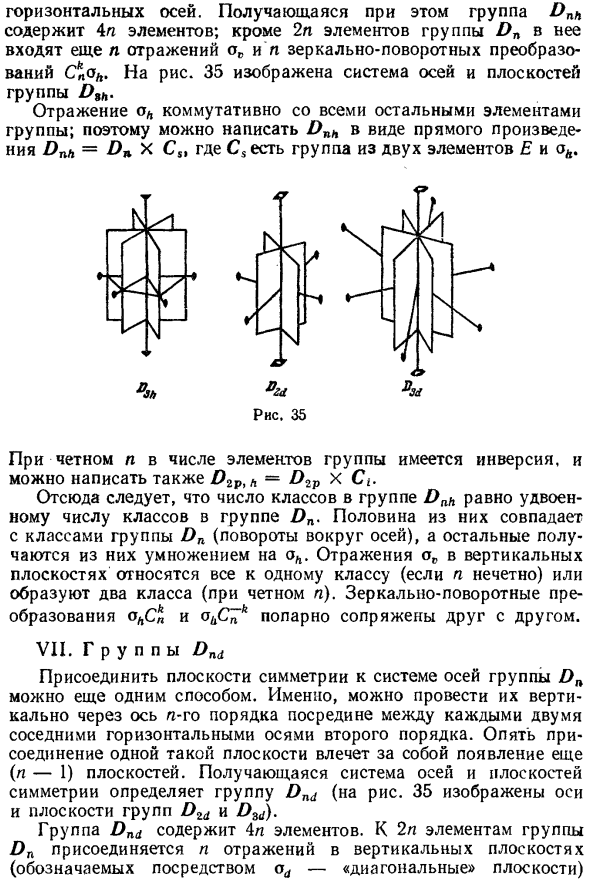
Группа результатов na D nh содержит 4n элементов. Исключить 2n элементов группы D n Также включает в себя n отражений ov и n поворотов зеркал Формация 35 показывает систему осей и плоскостей Группа D кость ^. / • ♦ & Д 2 д Рисунок 35 Отражение взаимозаменяемо со всеми другими элементами mi group, поэтому D nh можно записать непосредственно как производную Ссылка D nh —D n x C s, где C s — группа из двух элементов E И че Даже п, инверсия является одним из элементов группы, Вы также можете написать -D 2P x Ci.

Следовательно, число классов в группе D nh удваивается. Количество классов в группе D n • Половина матчей 446 Т Е Р И Й С И М М ЭТРИ И ГЛ. XII Имеет класс группы D n (вращение вокруг оси), остальные Излучается от них путем умножения отражений по вертикали Все плоскости принадлежат одному классу (если n нечетно) Или сформировать два класса (даже n). флип Различные преобразования σ ^ 1 C1 ^ и ahC ~ k Друзья. VII.

Группа D Прикрепите плоскость симметрии к системе групповых осей Py D n может быть другим. Т.е. ты можешь держать их Проходит вертикально через n-ю ось посередине между каждым Вторичные две смежные горизонтальные оси. Опять же, чтобы установить такой самолет, Более (n-1) внешний вид лица. Результирующая система координат Плоскость симметрии определяет группу D nd (рис. 35).

Оси и плоскости групп D 2d и- ^ 3Co * отображаются Группа D nd содержит 4n элементов. 2 p Для группировки элемента Py D n объединяет n отражений в вертикальной плоскости (Обозначается «диагональным» лицом) и n предварительно Форма формирования G = U2 (Jd- для выяснения природы Обратите внимание, что в последнем случае U2 может вращаться в соответствии с (91.6). Используйте формат U2 =.

Где av — вертикальное отражение. Плоскость, которая проходит через указанную вторичную ось. Тогда G = cr ^ crg (преобразование ов, само становится чи После групповых элементов, конечно, нет). Так как самолет Отражения av и пересекаются друг с другом вдоль n-й оси Формируем порядок, угол (tg / 2 n) (2 k + 1) (k = 1). , , , (N-1) (по Здесь угол между соседними плоскостями равен 7g / 2n) Далее, согласно (91.6), 2 n®d- & d & h ‘~ / 2 n®d- & h & d’ ~ / 2 n®d- & h ‘-‘ 2 n- ^ 2 n

Применяя эти соображения к группе D 2p, d-> Следующие 2p + 3 класса включены: E, ось p- Далее два сопряженных класса вращения вокруг (р-1) Коаксиальный, класс 2р C / 2 виток, класс 2р отражение и р Два класса преобразования вращения зеркала. Если группа имеет нечетное число n (n = 2p + 1) Инверсия (это Ось в этом случае перпендикулярна вертикальной плоскости).

Так что если мы напишем D 2p + 1, d-> 2p + 1 x, группа D 2p + i, d содержит 2p + 4 класса, полученные непосредственно Из класса p + 2 группы D 2p + iVIII. Группа Т (Группа Терратра Эдра) Эта система групповых осей является системой осей симметрии тет Reidora. Его можно получить, добавив в систему координат.

Группа V 4 наклона Третичная ось, вращение Вокруг него 3 оси Второй порядок друг другу. Эта система осей удобна Твист рисует 3 оси второй Приказ пройти Центр противоположной поверхности Куб и кубическая ось Как пространственная диагональ Этого куба На рисунке 36 показано расположение этих осей в кубе. И тетраэдр (одна ось каждого типа). Вторичные три оси эквивалентны друг другу. ось Третий порядок конвертируется таким же образом.

Другие поворачивают C2, но они не двухосные. 12 элементов группы T будут распределены 4 класса: E, 3 хода C2, 4 хода C3 и 4 оборота с . IX. Группа d T d В эту группу входят все тетрасимметричные преобразования. Edora. Система осей и плоскостей может быть получена путем добавления: Ось группы T плоскости симметрии, каждая Он проходит через вторую ось и третьи две оси.

в Эта вторичная ось вращает зеркало Четвертичная ось (как это происходит) Группа D 2d) — полезно представить эту систему Ось вращения через центр 4 кубических оси, похожих на противоположную сторону куба; Его пространственная диагональ, 6 плоскостей симметрии C3 C3 С2 С2 Рисунок 36 448 Т Е Р И Й С И М М ЭТРИ И ГЛ. XII Sz ? 4 _ Пройдите через каждую пару противоположных краев (верх Рисунок 37 показывает одну ось каждого типа и является плоской Стиль).

Плоскость симметрии На третичной оси последняя является двусторонней Ось. Все оси и плоскости каждого эквивалентного типа Это было записано. Таким образом, распределение 24 групповых элементов Дается в пяти классах: E, 8 в Воротов С.З. и С. |, шесть отражений в плоскости, 6 S4 зеркальных преобразований И S4, 3 витка C2 = S . X. Г р п р а т ч Эта группа Т Центр симметрии T ^ = T x C {.

В результате Они выглядят три перпендикулярно друг другу Плоскости симметрии, проходящие через каждый Ось 2-го порядка и ось 3-го порядка Ряд становится зеркальной осью вращения 6-й порядок (рисунок 38 показывает Из этих осей и плоскостей). Группа содержит 24 элемента и распространяется 8 классов, прямой прием Группа Т класс Ся Xi. G p u p p O O (g p p o o k t e d r a) Эта группа систем координат является системой координат.

Куб Rii: три четвертичных оси проходят через центр Лицом к лицу, 4-й оси 3-го порядка — через Противоположная вершина и 6 вторичных осей Разрез в центре противоположного ребра (рис. 39). Sz С2 Я Vj. / с. 9 носок Рис. 38 Рис. 39 Легко видеть, что все оси в одном и том же порядке эквивалентны Каждый из нас двусторонний.

Поэтому 24 элемента кружева Разделены на 5 классов: E, 8 витков C3 и C |, 6 Витки С4 и С |, 3 витка С \ и 6 витков Сч- XII. О группе Это группа всех симметричных преобразований куба 1). Это получается путем добавления центра симметрии к группе O. Oh = O x C i. Третичная ось группы О-поворот С другой стороны, ось вращения зеркала шестого порядка (около Странная диагональ куба);

6 плоскостей симметрии через каждую пару Противоположный край и три плоскости, параллельные грани Куб (рисунок 40). В этой группе 48 предметов 10 классов, которые можно получить напрямую Из группы О класс. То есть 5 соответствует классу группы. Пи О, и другие: /; Восемь Зеркало Преобразование Sq и 5 |; 6 зеркальных поворотных преобразований C C ^ CThi C \ & h вокруг четвертой оси, три голоса Ab в плоскости, параллельной оси 4-й порядок;

6 отражений в плоскости ov, верт По отношению к этим осям. XIII, XIV. Gruppy Y, Y h (группа, которую я представляю) Эти группы по сути работают как сим-группы. Молекулярная метрика только в исключительных случаях. Поэтому мы Ограничить показ, что Y — группа из 60 ходов.

Товарищи вокруг оси симметрии икосаэдра (обычно 20 Треугольник никнейм) или пятиугольник додекагон эдра (12 правильных пентаэдров), 5-й порядок 6 осей, 3-й порядок 10 осей, 2-й порядок 15 осей Горн. Группа Y h получается путем добавления центра симметрии. Y h = Y x C, представляющий полную группу преобразований Симметрия этих многогранников.

Это исчерпывает все возможные типы групп точек, Содержит конечное количество элементов. В дополнение к ним Рассмотрим так называемое непрерывное облако точек Py, содержащая бесконечное количество элементов. концы 8 98.

Смотрите также:

• Решение задач по физике

Преобразования симметрии	Представления групп
Группы преобразований	Неприводимые представления точечных групп

Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.