Энтропия

Энтропия

• Энтропия Далее обратимся к математической формулировке второго закона. Во-первых, мы устанавливаем эффективность 1 вспомогательный statement. By обменивающ жару с множественными резервуарами с температурой Tv T2, несколько систем обеспечивают что процесс c циркуляции завершен. Соответствующее количество тепла Qv Q2,…Согласитесь, что

система Qn заменит резервуар алгебраической величиной и рассмотрит положительное и отрицательное тепло, которое поглощает система. Докажем справедливость следующей зависимости. +(2.26) ’ 1 ′ 2 * P С этой целью бак телевидение Т2%…. Рассмотрим другой процесс, Cob*\, который состоит из N обратимых процессов Карно, которые происходят между новым баком Tn

и температурой TQ, и этот 2-й процесс возвращает тепло Qv Q2 и Qn в бак Tv T2. Поэтому в результате сложного процесса C-f-Co6p состояние всех N резервуаров не изменяется. Между тем, нагрейте N часть Qq …, Qq0, или всего (2.2 7） •- 2Вт я-1 Кроме того, поскольку процесс СОБР обратим, все Q(01) определяется соотношением. (2.28） (2.29） Ци _ Т { <То время’ Итак, согласно (2.27)и (2.28)、 Деньги. — о J• Это Конечным результатом является то, что определенное количество

Однако, согласно 2-му закону (формулировка Кельвина), это значение может быть только отрицательным： Людмила Фирмаль

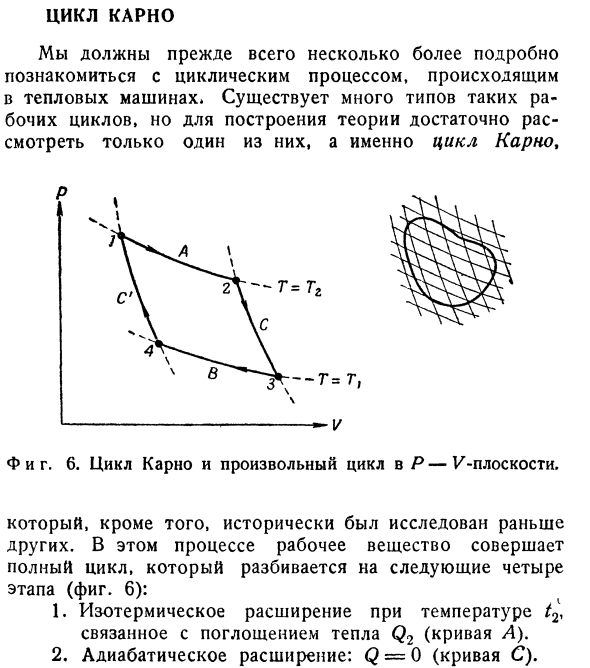
тепла Q0 извлекается из 1 бака при температуре T0. (2.30） Если вам нужно доказать. Равенство (2.30)относится к случаю, когда процесс C также обратим. В приведенном выше доказательстве мы использовали отдельный набор резервуаров, но на рисунке 1, Рисунок 6 показывает, как

настроить любой круговой процесс в цикле Карно. Если температура изменяется непрерывно, то можно представить, что процесс осуществляется с помощью непрерывной серии тепловых резервуаров, причем из каждого резервуара система поглощает небольшое количество тепла dQ. Тогда соотношение(2.30) принимает вид: (2.31） Где φ обозначает Интеграл всего цикла. Равный cst

относится к обратимым процессам. Это соотношение позволяет вводить новые государственные функции и entropy. To подтвердив это, рассмотрим обратимый циклический процесс, показанный на диаграмме P-Y. И фигура тоже. 7.Согласно теореме (2.31)、 ДЖЕЙ ДЖЕЙ ^ =(2.32） Я 2 (по) (по б） То есть, Интеграл Два 1 ^^ 5（2）-5（1）（2.33） 1. Таким образом, для каждой точки На диаграмме состояния

• мы определили значение функции S-S (Pt V), называемой энтропией. Энтропия определяется до того П. С. Два (2.34） (2.35） И фигура тоже. 7. Это константа, но эта константа, очевидно, может быть найдена путем выбора некоторого состояния (P0V0) в качестве начального состояния. Если 1 процесса, например 1 — > 2 необратим, то вместо соотношения (2.32) возникает неравенство(2.31). /«+/„£<0.1 2 Или J в ^ Ф „<$ 2-1 Физический смысл этого неравенства особенно

ясен в случае процесса изоляции (dQ = 0).И затем… 52> 5г(2.36） Другими словами, если процесс 1 — > 2 происходит спонтанно, то энтропия конечного состояния 2 должна быть больше энтропии начального состояния. В этом смысл утверждения Клаузиуса о том, что “ энтропия Вселенной стремится к максимуму.„Спонтанные изменения в адиабатически замкнутых системах всегда происходят

в сторону увеличения энтропии. В“ открытой “ системе энтропия также может уменьшаться, но в этом случае такие изменения всегда происходят в окружающих объектах, что приводит к увеличению общей энтропии системы

Важно помнить, что формулировка второго закона термодинамики как закона увеличения энтропии применима только к адиабатически замкнутым системам в таком виде. Людмила Фирмаль

и окружающих объектов. 1.Неравенства Клаузиуса здесь рассматривается система теплового контакта с термостатом-это типичная схема, используемая в thermodynamics. In в этом случае взаимодействие системы с окружающими объектами характеризуется температурой Твнеш и давлением Явнеш. Константа

на поверхности системы. Из (2.35) следует, что в процессе поглощения системой количества тепла AQ от термостата изменение энтропии происходит следующим образом: Д(2.37） 1 пример Кроме того, согласно первому закону, если процесс предполагается спонтанным、 БК = бу + РВ » embV(2.38） Независимо от того, является ли это

обратимым процессом или not. So мы можем написать ^ ext. AS> в / + Летеш (2-39） Это знаменитое неравенство Клаузиуса. Если процесс обратим, то в (2.39) необходимо использовать равенство sign. In в этом случае система должна всегда находиться в равновесии при заданных внешних температуре и давлении. Однако если требуется задать (2.39) Tvnesh = T, то в случае знака равенства Yaviesh = I, а затем вывести

уравнение, связанное с параметрами состояния системы, приращение должно быть бесконечно малым. Полученное уравнение (2.40)） TdS = dU + PdV Конечно, это всего лишь определение энтропии, описанное в дифференциальной форме(2.33).Формула (2.40) называется

термодинамическим тождеством (1).Это основное уравнение, которое так или иначе охватывает как первый, так и второй законы термодинамики. Заметим, что из термодинамического тождества для частных производных можно получить следующее соотношение: При выводе последнего соотношения мы использовали формулу (1.19).

Смотрите также:

Предмет термодинамика

Примеры	Формулировки второго закона
Энтропия и вероятность	Цикл Карно