Оглавление:




Обработка результатов нескольких серий измерений
- Иногда множественные измерения одного и того же постоянного размера проводятся разными людьми, в разных условиях, в разных местах, в разное время и на разных этапах. Результат такого измерения определяется серией полученных значений, которые могут иметь разные статистические характеристики в разных ситуациях. Ряд называется однородным, если он состоит из значений, которые подчиняются одному и тому же закону распределения вероятностей.
В противном случае ряд считается гетерогенным. Проверка однородности необходима при выборе метода для совместной обработки нескольких наборов результатов измерений. Обычно организуется на уровне эмпирических моментов. Среднее арифметическое и оценка дисперсии для каждой серии сравниваются.
Если посадка не связана с системой отверстий или системой валов, отверстие должно иметь больший допуск, если допуски отверстий и валов не совпадают. Людмила Фирмаль
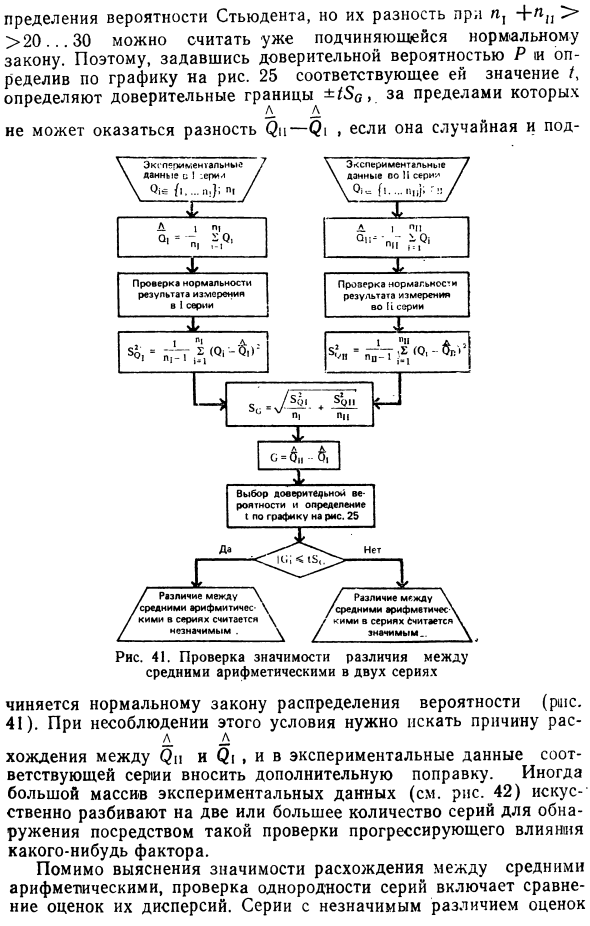
Разница между средним арифметическим R и pH двух разных серий может иметь среднее значение нуля и случайную дисперсию. o2 = — + в Zn- P * Если экспериментальные данные каждой серии следуют нормальному закону распределения вероятностей, среднее арифметическое ( 1 и He и его разность 6 = Pn — 0 нормальный закон) для многих из них (так называемые> 20 … 30).
Если в серии имеется небольшое количество экспериментальных данных, среднее арифметическое 0 и 11 следуют следующему закону: Распределение вероятностей студентов, но разность n1 + >> 20 … 30 можно рассматривать как следование нормальному закону, поэтому мы дали доверительную вероятность Рm, определенную согласно графику на рис. 5. 25 определяется соответствующее значение I, доверительный интервал, за пределами которого разность C — C не является случайной, Рисунок 41. Подтверждение важности среднего арифметического В двух сериях Следуйте нормальному закону распределения вероятностей (RSC. 41).
Если это условие не выполняется, вы должны найти причину несоответствия между C и 2 . И далее модифицируем экспериментальные данные для соответствующих серий. Большой массив экспериментальных данных (см. Рис. 42) искусственно разделен на две или более серии для обнаружения путем изучения прогрессивного воздействия какого-либо фактора. Помимо выяснения важности расхождений между средними арифметическими, проверка однородности рядов включает сравнение оценок их дисперсий. Серия с небольшими различиями в оценке Дисперсия называется эквидистантной и имеет большую разницу — не равную.
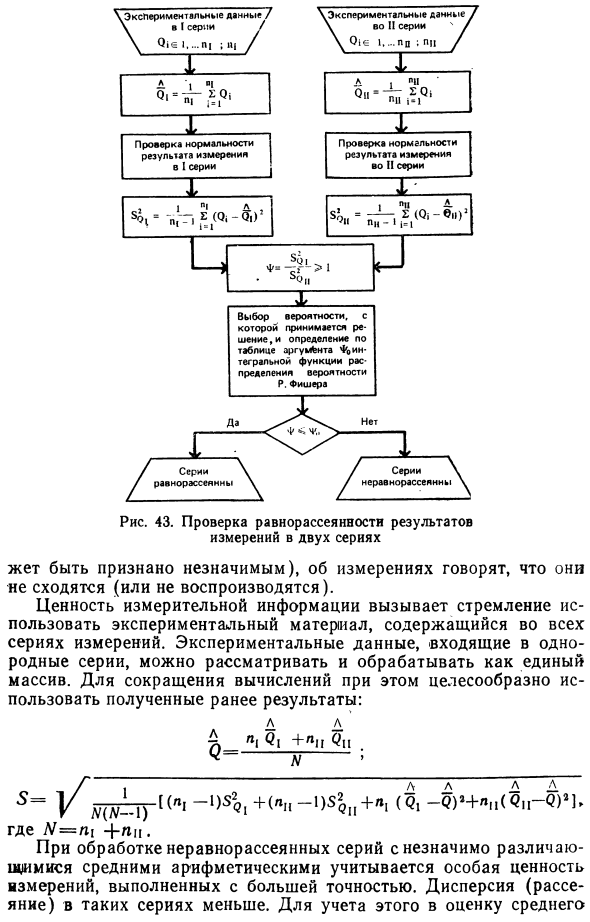
- Значимость различия между двумя сериями оценок дисперсии, которые измеряются в соответствии с нормальным законом распределения вероятностей, проверяется в указанном порядке. Здесь начальная операция соответствует операции, показанной на рисунке 43. 41 Следовательно, это выполняется один раз при проверке однородности ряда. В ходе расчета формируется соотношение и его вероятность больше 1. R, если это число случайное. A. Следуйте распространению Фишера. Следовательно, Р.
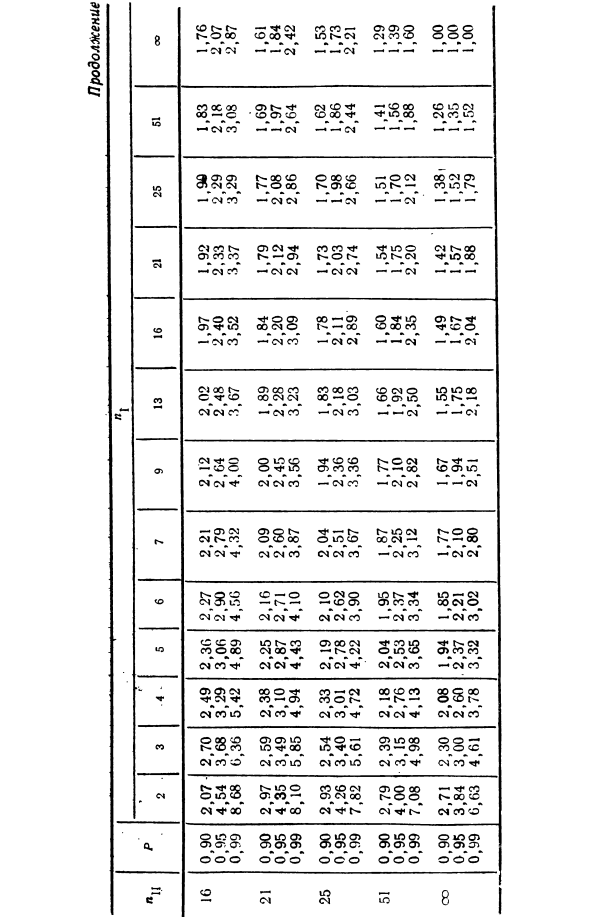
Предположим, что с выбранной вероятностью P гипотеза о равной дисперсии ряда согласуется с результатами критерия Р. А. Фишера. В противном случае эта гипотеза должна быть отвергнута. Значения аргументов интегральной функции распределения вероятности Р. А. Фишера приведены в таблице. 14. Равномерно разбросанные серии с небольшими различиями арифметических средних считаются однородными. Если содержащиеся в них экспериментальные результаты получены при одинаковых условиях, это свидетельствует о сходимости измеренных значений и воспроизводимости при разных условиях.
Относительное измерение-это измерение того же значения, которое играет роль единицы измерения, или значение отношения к измерению, которое связано с тем же значением, принятым для оригинала. Людмила Фирмаль
Сходимость означает измерение качества, которое отражает близость, воспроизводимость и различные местоположения (разные местоположения, разное время, разные методы и средства) результатов, выполненных в одних и тех же условиях. Если ряд неоднороден (неравномерно разбросано или среднее арифметическое различие Рисунок 43. Подтверждение равномерной дисперсии двух серий результатов измерений Это может считаться незначительным), и считается, что измерения не сходятся (или не воспроизводятся). Ценность информации об измерениях проистекает из желания использовать экспериментальный материал, включенный во все серии измерений.
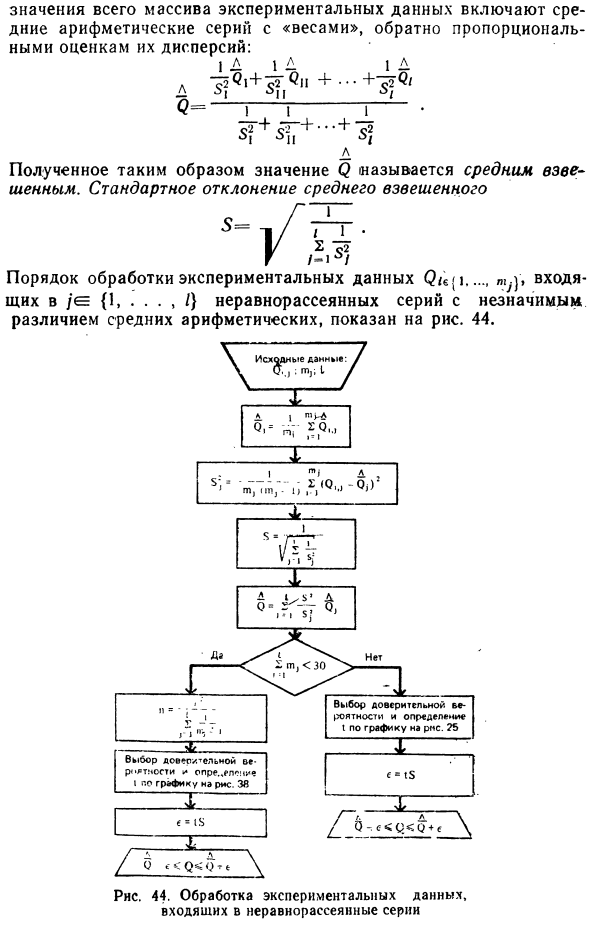
Экспериментальные данные, содержащиеся в однородных сериях, можно рассматривать как единый массив. Мы рекомендуем использовать ранее полученные результаты для сокращения расчетов. т. I 0, + 5 (1 N 5 = N (N-1) (I -1> 5 1+ nn- ) 5Cn + 1 31- ) + (5ts-5) b Где ^ = n ^ + шт. При обработке неравномерно распределенных рядов с немного отличающимися средними арифметическими значениями учитываются специальные значения для измерений, выполненных с более высокой точностью. Такая серия имеет небольшую дисперсию (рассеяние). Чтобы объяснить это в среднем Таблица 14.
Значение всего массива экспериментальных данных включает в себя среднее арифметическое число с весом , который обратно пропорционален оценке дисперсии. Полученное таким образом значение С называется средневзвешенным. Средневзвешенное стандартное отклонение Порядок обработки экспериментальных данных …….. тд, ввод- в / е 1 ,. , На рис. 1 показан неравномерно распределенный ряд с небольшим различием среднего арифметического. 44. \ Them 7 -… Рисунок 44. Обработка экспериментальных данных. Включено в Неоднородная серия Это можно считать незначительным , и считается, что измерения не сходятся (или не воспроизводятся).
Смотрите также:
| Однократное измерение | Воспроизведение единиц физических величин |
| Многократное измерение | Передача информации о размерах единиц средствам измерений |

