Оглавление:











Атом водорода в электрическом поле
- Атом водорода в электрическом поле В отличие от других уровней атомов, уровень атомов водорода мов, в однородном электрическом поле они испытывают раскол Пропорционально силе поля (линейный эффект Затвор). Это связано с присутствием водорода Денатурация чая в зависимости от различных условий Значение I (заданное главное квантовое число n) Дайте ту же энергию.
- Дипольный матричный элемент. Между этими состояниями никогда не бывает момента перехода Равно нулю, но секулярное уравнение уже первое Приблизительное значение — ненулевой сдвиг уровня1). Для расчета полезно выбрать волну без возмущений. Матрица возмущений Диагональные линии для каждой группы вырождаются друг в друга Государство.
Это оказывается сделано квантовым Атом водорода в параболических координатах. Людмила Фирмаль
Волна стационарная функция vviin2ra атомов водорода в воде Параболические координаты определяются по уравнению (37.15). (37.16). 1) Следующий расчет не учитывает тонкую структуру Сильный уровень. Так что поле не сильное, Применимость теории возмущений), но в то же время Расщепление Кобо было отличным по сравнению с микроструктурой.
Если нет — см. Вопрос 1, §52 тома IV. 356 ATOM GL X Оператор возмущения (энергия электрона S поля) Sz = £ (£ -7 7) / 2 (поле направлено положительно, действие Сила, действующая на электроны, находится в отрицательном направлении Ось z) 1). Я заинтересован в переходных матричных элементах \ \ П2 — п ^ пп ^ тт при которой энергия (т.е. Число n) не меняется.
Легко увидеть, что произойдет. Ненулевые диагональные матричные элементы ОО ОО 27G j ^ | V; nin2m | S z d V = —J ^ jj * (£ Tf) \ FTn2Gn \ dt; drj = 0 0 0 00 00 = f / f fnim (pi) fn2m (p2) (pi-p ) dPl dp2 (77,1) 0 0 (Использовалась замена £ = npi, r] = np 2). О ци Диагональ исследуемой матрицы ясна. какие Число n \, P2, то по диагонали о них Из взаимной ортогональности разных функций То же самое, что и nn (см. Ниже).
Интеграция DPI (77.1) отделены dp2. Интеграция результата Дано как математическое дополнение к f (целое число (f.6)). позже Простой расчет, полученный в результате первой модификации Приближение уровня энергии 2) E i1) — ^ Sn (ni-P2) (77,2) Или в нормальных единицах = -n (n i-P2) | e | £ -> Ц. 2 их Два крайних компонента уровня разделения n \ = n-1, P2 = 0 и n \ = 0, P2 = n-1.
Расстояние между ними Согласно (77.2) два крайних уровня 3Sn (n-1), То есть общее деление уровней под влиянием Тарка примерно Это пропорционально n2. Увеличение резки из-за основного кванта Натуральное число: чем дальше от ядра, тем больше электричества Трон, атомный дипольный момент велик. х) В этом разделе используются атомные единицы.
2) Этот результат основан на старой квантовой теории и Паули Используя Шредингера (1926) квантовая механика. Наличие линейных эффектов означает Атомные состояния имеют дипольный момент со средним значением Читать Это согласуется с тем, что в состоянии, определяемом Параболическое квантовое число, распределение заряда Атом не симметричен относительно плоскости z = 0 (см. § 37).
Поэтому, когда η> P2, электроны в основном 100 Роне положительный 2, так что дипольный момент атома Противоположная сторона внешнего электрического поля (заряд электрона отрицателен!). В предыдущем абзаце вы Рождение однородного электрического поля Завершено — остается как минимум вдвое больше денатурации Состояние с другим знаком проекции момента в направлении.
Поле (в этом случае мгновенная проекция указывает состояние, Равен = б). Однако из уравнения (77.2) линейная Даже с этим устранением вырождения, эффект Штарка водорода Не достигнуто, сдвиг уровня (когда заданы n и n \ -P2) Нет зависимости от га и P2-дальнейшее устранение вырождения Происходит с эффектом второго приближения. Рассчитайте это Это особенно эффективно n \ = P2 линейного эффекта тартарка обычно нет.
Неудобно использовать для подсчета вторичных эффектов Чтобы использовать нормальную теорию возмущений, Вам нужно обработать бесконечную сумму сложных форм. Вместо этого используйте следующее с небольшой модификацией По-новому. Уравнение Шредингера для однородных атомов водорода Электрическое поле имеет следующую форму.
Разрешить разделение переменных, как в уравнении £ = 0 В параболических координатах. Та же перестановка (37,7) §37 приводит к двум уравнениям (77,3) (77,4) В отличие от (37,8), наличие членов с £. рассматривать Эти уравнения определяют энергию E в качестве параметра. Значение определения и количество /? х, /? 2- как собственное значение 358 ATOM GL X Значение соответствующего оператора (который легко проверить Эти операторы являются самостоятельными).
Эти величины определены При решении уравнения как функции E и £, тогда Состояние /? 1 + /? 2 = 1 определяет энергию как внешнюю функцию Поле. В приближенном решении уравнения (77.4) Возьмем член, содержащий поле £, как небольшое возмущение. В нуле Приближенное (£ = 0) уравнение шения / i = \ D / m r (k), h = y / sfn 2m (v £), (77,5)
Где функция f nirn такая же, как (37.16), вместо энергии параметры £ = y / -2 E. (77,6) /? Я /? Соответствующее значение 2 ( n необходимо заменить на 1 / е (37.12) <= („, + H ± i) e, = („ 2 + M ± i) £. (77,7) Функция с разными значениями n \ для конкретного e inter / 1 Но оно ортогонально, так как все самостоятельные собственные функции Жена оператора (мы уже используем этот факт Нормализуется (77.5) при рассмотрении линейных эффектов);
Наши условия Oh Oh Oh J ф? d £ = 1, J f l d -j = 1. 0 0 (3 \ и /? 2 определяется первая поправка приближения Диагональный матричный элемент возмущения Oh Oh Oh p p = f / £ 2 / i число = -f / V2f l d V. Ах ах расчет / 3 ^ = — ^ — (6n \ + 6 ni \ m \ + m 2 + 6ni + 3 | m | + 2). (3 ^ выражение отличается от замены n \ с P2 и переменной Войти.
Во втором приближении, согласно общей формуле: Теория возмущений, n (2) _ 8 2 l «2) m„ i | 2 1 «16 2 ^ ^ 0) (n i) — ^ 0) K)’ Интегральный элемент матрицы (^ 2) П1П’1, рассчитан Они находятся в математическом дополнении §f. Только ненулевой элемент (£ 2) r c, ni -1 = (£ 2) n i-i, n i = — ^ (2 u + \ m ) ^ / ni (ni + \ m ), (£ 2) n i, n i-2 = (£ 2) n i-2, n i = ~ ^ V n i (n i-l) (m + \ m ) (ni + \ m \ -1).
Стоя в знаменателе разность равна / 3i ° V i) — / 5i0) K) = e (ni-ni). Результатом расчета является / 3 ^ = — ^ rm (1sh 1 + + l) [4m 2 + 17 (2 | m | ni +) I-2px I- |? P | I-2? Т / ч) Н-18] ((32 выражения меняются путем замены n \ на n 2) Относительное выражение / 3 \ + (32 = 1, Получить уравнение en- ^ r [17n2 + 51 (ni-n2) 2-9m2 + 19] + — £ ^ (n1-n2) = 1.
Решение по последовательному приближению дает ВТО В приближении энергии E = –e2 / 2 формула E = — + + -пn (n \ -n 2) — n4 [17n2-3 (ni-n 2) 2-9m 2 +19]. 2р 2 16 (77,8) Второй член линейный Абсолютный эффект. Третий — желаемый вторичный эффект. (Г. Венцель, И. Уоллер, П. Эпштейн, 1926). Это Порядок всегда отрицательный, то есть из-за вторичного эффекта Терминология всегда смещается вниз.
- Средний диполь Производная момента получается путем дифференцирования (77.8) по полю. В состоянии n \ = n 2 оно равно dz = (n4 / 8) (17n2-9 t2 + 19) 5. (77,9) Следовательно, поляризуемость атомов водорода в нормальных условиях (N = 1, m = 0) равно 9/2 (см. Также вопрос 4 в §76). Абсолютное значение энергии водородного члена быстро Увеличивая главное квантовое число n, Старк Раскол увеличивается.
В этом отношении интересно Эффекта Штарка на сильно возбужденных уровнях Очень мощное поле, разделение, которое они создали 360 ATOM GL. X Энергия самого уровня и, следовательно, такая же величина, как в теории Помехи не применяются 1). замена f i = X i / ^ A, f2 = X2 / yfn (77.10) Уравнение (77.4) д xi. (E 01 t-1 £ L _ W (2 + J ~ ^ ~ i 4 xi-0 ‘ + L на C | + A _ m! ^ я £ \ „ V 2G) 4P 4 7 (77.11) др] V 2 г] ат]
Это можно сделать с помощью Квазиклассическое состояние с большим значением n. Людмила Фирмаль
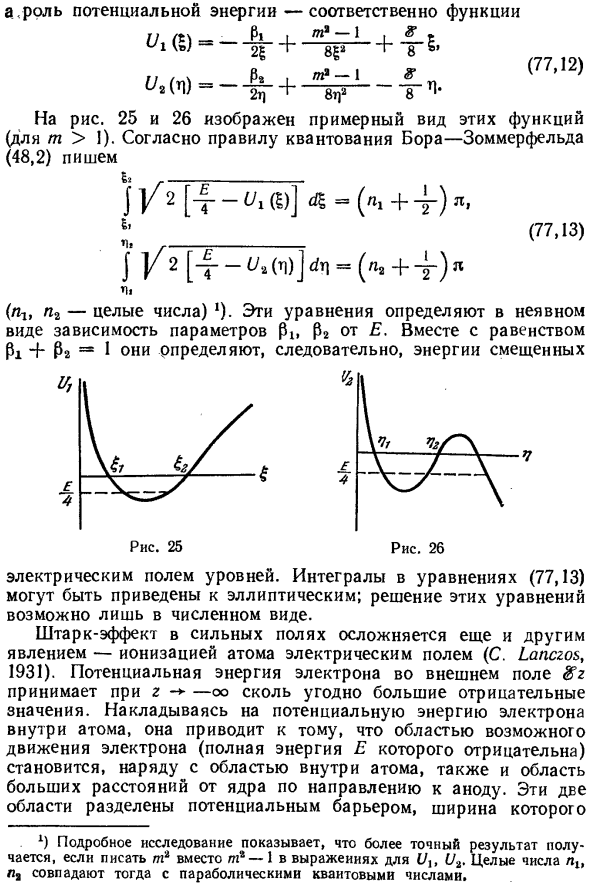
Однако каждое из этих уравнений имеет вид одномерного уравнения Шредингер, а роль полной энергии частиц, играет E / 4 Следовательно, роль потенциальной энергии является функцией r w = -§ + ^ u (n) yi = — & + 2CH1 -2g? , T] 8 г] 8-ч-г (77’12> На рисунках 25 и 26 показаны примеры этих функций. (Если m> 1). Согласно правилам квантования Бора-Зоммерфеля Да (48.2) В ^ [E / A-u ^ W = (u + 1/2) n, 6 м ^ / 2 [E / 4-U 2 (v) \ dv = (n 2 + 1/2) n м (Ni и P2 — целые числа) 2). Эти уравнения неявно определены Параметр f? х, ф?
С равенством зависимостей от 2 до Е s2 / A / 2 / (77,13) 1) Малость требуется для теории возмущений высокого уровня Помехи только по сравнению с энергией самого уровня (энергия связи) Е), а не интервал между уровнями. Конечно, квази Классический чехол (сильно возбужденный Условие) нарушение можно считать малым, если сила, которую оно вызывает, мала Малая по сравнению с силой, действующей на частицу при отсутствии возмущения Система, однако, это условие эквивалентно выше.
2) Согласно детальному исследованию, более точные результаты являются средними [Происходит, когда mn2 записывается вместо mn2-1 в выражениях D и U2. Все Числа u и n2 совпадают с квантовым числом параболы. /? 1 + /? Поэтому 2 = 1о ™ определяет энергию для движения Уровень электрического поля. Интегрирование уравнений (77.13) Это может быть уменьшено до эллипса. Решите эти Только в числовом формате.
Эффект Турка в сильном сильном поле осложняется другим Феномен-атомная ионизация электрическим полем (C. Lanchos, 1931). Потенциальная энергия электронов Во внешнем поле Ez равно 2-) ►- Любое большое отрицательное значение Чтения. Потенциальный дубликат Энергия электронов в атоме, это Приводит к тому, что это возможный район Электронное движение (полная энергия E Отрицательное значение)
Сделайте это в области внутри атома или в области большого расстояния От ядра к аноду. Эти две области разделены Ширина является потенциальным барьером Уменьшается по мере увеличения поля. Но для Квана Всегда есть несколько механизмов Ненулевая вероятность частиц Пройдите потенциальные барьеры.
В дан В случае г-на электронный выход из зоны Внутри атома, который проходит через внешний барьер Это не что иное, как ионизация атомов В слабом электрическом поле вероятность такой ионизации исчезает. La, но он растет в геометрической прогрессии с полем и полностью Сильное место важно 1). Z a z h 1.
Определить вероятность ионизации (в единицу времени) атомов воды Введите в электрическом поле, которое удовлетворяет условию (основное состояние) См. 8 Г) о, волновая функция Квазиклассические. С другой стороны, форма уравнения (2) имеет вид Sh Redinger формулу, вы можете использовать следующую формулу ми (50,2). Требовать f, чтобы соответствовать волне в качестве граничного условия r) = 77
Новая функция (1) для 0, получить выражение в области вне барьера X = -) ^ оболь V / 2 “p | — (C +, • + [J, r7T V0 где p (r}) = от \ 1 до — + — + — 2 + — • | 4 2g) 4i f 4 Меня интересует только квадрат | x | 2. Следовательно, мнимая часть показателя Несущественный. Показать корень уравнения p (rj) = 0 / м \ Ixl2 = ^! ^ exp (- £ -2 / U *? — 7? 0) — (3) » 70 ‘ Для предэкспоненциального множителя установите r] 1 B0 |
Для показателя степени x e следующий член в расширении функции p (ij): / V I VI \ x | 1 = J ^ t = r «p (~ {» / ‘/ ΓGпM * / — «) • х) Эта проблема использует атомные единицы. Где r] 1 = 1/8. Интегрируя и игнорируя, где бы вы ни были Вероятно, D) o8, по сравнению с единицей lx | 1% £ v 7 ^ T «P (~ {_ i) ‘<4) суммарный поток с вероятностью прохождения через плоскость, перпендикулярную оси z.
То есть желаемая вероятность ионизации w Я 2v z2npdp о (P — цилиндрический радиус указанной плоскости). Большой г) и ма Loh £ можно поставить дп = к Заменить электронную скорость Мы получаем последний w = J \ x \ 2 ^ ~ о w = r ^ v h) (5) Или в нормальных единицах, 4ш 3 | е | 9 (2 т 2 \ е \ ‘ w = ——- = -exp 8 P7 * V 38 P4 2.
Определение вероятности извлечения электрона электрическим полем Из потенциальной ямы с коротким расстоянием, где существуют электроны Связанное состояние. Электрическое поле считается слабым. \ e \ 8 кр 1). На этих расстояниях Волновая функция связанного состояния электрона в яме (без поля 8) имеет вид асимптотический A ^ [n _ f = ——— e — e> cr г
Где A — безразмерная константа для моего конкретного типа1). В параболических координатах r = (£ + 77) / 2, область r) £. Волновая функция принимает форму 2 AyJ ~> c гр «——— exp (6) 1) Так что, если радиус ямы очень маленький, ой. 2 Удовлетворите первую формулу (приблизительно 77,11, если £ мало). Тогда = -1/2 и для определения зависимости φ от rj имеем следующее уравнение: 0 + (4 «i + 3? + F ‘,) x = o’ x =
Если уравнение (2) решается так же, как было решено, вместо (3) VI далее / \ 1x | 2 = 4 A ^ exP (- £ ~ 2 [U * 7- »7 °), Vo P \ J J Кроме того, вместо (4) ,, 2 A £ (, 2 1×1 = / 0 л EXP y / Sri-1 V sS И, наконец, вместо (5) w = 7rA 2 £ exp (- \ 3 ^ Или в нормальных единицах, tg | e | EA2 (2H2x b w = ——- e x p ————— H> c y 3r | e | £, 3. Экспоненциальная оценка вероятности разрыва Электроны из потенциальных ям под действием равномерных переменных.
Электрическое поле S = So cos ut \ частота и амплитуда Поле удовлетворяет условию Не <\ E \, \ e \ So <Я2х3 / рн, Где yn = y / 2m \ E \ / H, \ E \ — энергия связи электрона в яме (J1, В. Келдыш, 1964 г). г) Например, можно говорить об отрицательно заряженной одиночной ионизации Ионы сильными световыми волнами, в этом случае создаются потенциальные дыры.
Из-за взаимодействия между электронами и нейтральными атомными остатками. состояние Ни один из \ E \ не гарантирует справедливость классических соображений Электромагнитное поле Вероятность разрыва w при данных условиях Экспоненциально маленький. Рассчитать только экспоненту.
Вы учитываете только два (без предварительного экспоненциального фактора) Как одно направление поля измерения, ось Z. Здесь электрическое поле не является скаляром, Векторный потенциал: A z = A = — (cEo / u) sm u t. Тогда гамильтониан Электроны вне ямы g> 1 / k d | e | £ o. \ 2 H = —- я — в н … — b-s m u t I 2 га V д з а) (См. (111.3) ниже), координаты z не включены.
Введя безразмерную ручку Переменные и безразмерные параметры n _ 2m u hu \ e \ mSo r = —— 1, m = 2ycz, VI = —— = —-, F = 2ha ’Mon2 | E \ ‘P2>? » Запишите уравнение Шредингера в виде я д е / д, я Ф. _ V т ——- = ——— 1 —— sin ft r F. 4 dt \ dt] Q Граничное условие этого уравнения rj-> 0, решение Φ (v, m) согласуется с непертурбативным полем по волновой функции За счет электронов в колодце (энергия E = — | .E |) As Φ-r]] -> 0. (7) Ищите решение, которое учитывает квазиклассическую природу проблемы (экспоненциально ) Φ = expz * S, где S (tj, t) — классическое действие.
с того времени Гамильтониан не зависит от координаты tu и обобщенного импульса Pn = P Потому что он сохранился по классической траектории, S = -J H (p, t) d r + r] p + A, H (p, t) = 4 ^ sin, (8) к Где А постоянная Кроме того, как функция действия в смысле действия Динатос (я, см. §43), вам нужно понять значение, которое ведет траекторию на p.
Определите и определите p как функцию от rj и m в данной точке rj в момент m Это выражается уравнением движения d S / d p = const. G] = g r s 2 Lt, (9) Д-р тогда (Константа выбрана так, что rj = 0 для m = тогда). Уравнения (8) и (9) имеют вид Действия, которые зависят от двух констант: А. И чтобы найти решение, Если условие (1) выполнено, это необходимо (например, при нахождении общих интегралов).
Уравнение Гамильтона-Якоби-I, ссылаясь на § 47, рассматривая A как функцию от Координатные и временные функции определяются условиями 1 ^ = 0. (10) от Очевидно, вам нужно установить A (m0) = затем. Тогда r] = 0 и m = тогда S = t, т. Е. S = m, существует согласно условию (7). Равенство (10) сейчас Совместим как H (p тогда) + 1 = 0 (1 1) 366 ATOM GL X Уравнения (9) и (11) вместе определяют функцию, (r], r) и p (r], r).
Волновая функция Φ (τ7, τ) одна (после подстановки (8)). Требуемая вероятность w пропорциональна плотности магнитного потока вдоль оси z. В классически доступной области эта плотность равна t> z | \ I / | 2. Начало этого Площадь определяется точкой, в которой lm S перестает увеличиваться. (<9Im S / dr]) Поскольку T = 0 и dS / dr] = p, из lm p = 0; (9), (1 1) Далее здесь x e и Rep = 0.
Из этого условия определяется стоимость. (1 1) Установить и получить р = 0 О 4F2 -2- sin Q t 0 = -1, Q Откуда Q_y / 2m \ E \ 2F ~ \ e \ (Мнимый «момент времени» представляет нереальную классику Целостность процесса). в конце концов G Qtq = zArsh7, 7 = — = D D f 4 F 4 2 11 ‘exp <—2 lm I sin2 fir dr’ + to>, Для м — любое действительное значение (мнимое число) Часть интеграции от этого не зависит).
При расчете интеграла это выглядит так EXP-Щb) пирог / S = (1 + — ^ 2) пепел 7- 27 (12) Выражение ограничения функции / (7): / (7) 7 1 в 1, уу / / (7): 2 7 в 1 в —7. Предельное выражение w 7-> 0 соответствует вероятности извлечения cha. Яма потенциальной ямы с определенным месторождением. Уравнение (1 2) применяется, когда показатель степени велик. Для этого В любом случае, fojo «\ E \» требуется.
Смотрите также:
| Мультипольные моменты | Электронные термы двухатомной молекулы |
| Атом в электрическом поле | Пересечение электронных термов |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

