Оглавление:






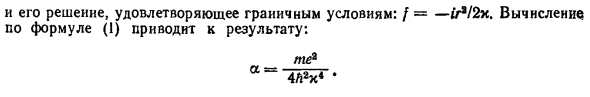

Атом в электрическом поле
- Атом в электрическом поле Когда атомы находятся во внешнем электрическом поле, Изменение уровня энергии, это явление называется эффектом Затвор. В атомах, расположенных в однородном внешнем электричестве Поле, мы имеем дело с электронной системой оси Симметричное поле (ядерное поле с внешним полем).
- В связи с этим, строго говоря, суммарный момент импульса атома равен. Больше не сохраняется, только полная проекция M j Момент J относительно направления этого поля. Другое состояние Мои значения M j имеют разные энергии. Электрическое поле устраняет денатурацию в направлении Милиционер. Тем не менее, этот вывод является неполным.
Разные условия Только по знаку M j все еще обладает той же энергией. Людмила Фирмаль
Конечно, однородные внешние атомы электричества Симметричный относительно отражения в любой плоскости. Проходит через ось симметрии (ось проходит через ядро Направление поля; ниже выберите в качестве оси z). Следовательно, государство Такие отражения требуют одинаковой энергии.
но При отражении на плоскости, проходящей через ось, Момент импульса вокруг этой оси меняет знак (по Положительная ось хода отрицательна Она включена). Предположим, электрическое поле довольно слабое Дополнительная энергия Маленький по сравнению с расстоянием между соседними уровнями По сравнению с ядерной энергетикой, по сравнению с тонкой Структура. Далее рассчитайте сдвиг уровня с помощью электр.
Вы можете использовать трическое поле и теорию возмущений. Разработано в § 38, 39. Оператор возмущения Равный энергии электронной системы в однородном поле, V = —d £ = — £ d z, (76,1) Где d — дипольный момент системы. С приближением нулевого порядка Уровень энергии вырождается (по направлению к общему моменту) Что); однако в данном случае эта денатурация не важна.
Применяя теорию возмущений, вы можете сделать следующее: При работе с невырожденными уровнями. Это после Количество dz в матрице (^ -подобная составляющая Только элементы других векторов) M j (см. § 29) изменяется без изменений, поэтому состояние Те, у кого значение M j, ведут себя при применении теории Нарушения не зависят друг от друга. §76 ATOM V E L E K T R I H E S K O M P O L E 351 Сдвиг уровня энергии в приближении первого порядка.
Представлены соответствующими диагональными матричными элементами Гнев Тами Тем не менее, диагональные матричные элементы Дипольный момент равен нулю (§75). Следовательно, раскол Уровень электрического поля является вторичным эффектом Полевой ряд 1). В качестве значения вторичного поля Уровень E p E p должен быть выражен как выражение вида AE n = — \ c $ £ i £ k, (76,2) Является симметричным тензором.
Выберите ось Z в направлении Поле, мы получаем AE n = — \ a ^ £ 2. (76,3) В то же время тензор поляризован. Атомный мост во внешнем электрическом поле. конечно Понимание общей формулы (11.16) с параметром A Если вы установите вектор и установите H = Hq-E {d { Значение электрического поля, индуцированного атомным дипольным моментом, составляет ~ I {n) _ DAEP 1 ~ дСи Подставляя здесь (76.2) 4)) = a ^ £ k. (76,4).
Поляризуемость должна быть рассчитана как Общие правила теории возмущений. По второму выражению Есть приближение (38.10) = -2 V ‘#) нм (t4) мин. (76,5) р к е п-е т у! T Поляризуемость атома зависит от его (невозмущенного) со Стоя с квантовым числом M j. Это последнее Зависимости могут быть установлены в общих чертах.
Другой способ Для различных значений M j Собственное значение оператора a \ k ~ a n $ ik + Pn {JiJk + JkJi ~ (76,6) х) Исключением является атом водорода. Неполе (см. Следующий параграф). водород Поле, где атомы других элементов достаточно сильны Очень возбужденный (таким образом, напоминающий водород, см. §68). Это общий вид тензора симметрии второго ранга. Из вектора J (см. § 75). Из (76,3) и (76,6) И E n = -y {«n + 2 / 3n [m} — \ J {J + 1)]}. (76,7)
- Сумма всех значений M j является вторым слагаемым Скобка исчезает, поэтому первый член перед Общее смещение «центра тяжести» делится Уровень. Также согласно (76.7), уровень c J = 1/2 — это кра- Мерсия (§60). Если атом находится в неоднородном внешнем поле Затем за пределы размера атома), то, возможно, существо Кроме того, эффект линейного разделения в области связан Нью-Йорк Квадрупольный момент атома.
Квадрупольный оператор Взаимодействие между системой и полем Классическое представление квадрупольной энергии (см. II, §42): V = \ ^ -Q ik, (76,8) О ОХГОХХК Где (p — потенциал электрического поля (средний Значение производной в положении атома). Z a z h 1. Определение зависимостей различных комарковых разбиений.
Компонент уровня мультиплета J Полезно изменить порядок комбинаций решений для решения проблемы. Людмила Фирмаль
Jamming, во-первых, без учета уровня Stark Представляя взаимодействие между тонкой структурой и спиновой орбитой. с того времени Атомный спин не взаимодействует с внешним электрическим полем и затвором Уровень расщепления в данный орбитальный момент L равен.
Выражение того же вида (76.2) с тензором c ^ *, выраженным через оперу Торус L like (76.6) представлен J. _ / —— ——— 2-2 OLik = aSik + b [L iL k + LkLi-— Sik ^ (Индекс n опущен.) После введения спина — орбитальное взаимодействие Атомное состояние должно характеризоваться полным моментом J.
Средняя Положение оператора ctik для состояния с заданным значением момента J (однако Его проекция M j) Выпуск 1 § 75. В результате, используя константы, вернемся к формулам (76.6) и (76.7) a, b, представленный константами a, b согласно соотношению _ _ 3 (JL) [2 (JL) -1] -2J (J + 1) L (L + 1) a = a, P = b ————————— m ——- ———— -. J (J + 1) (2 J-1) (2 J + 3)
Это определит зависимость расщепления от J (конечно, Не из L и S, а из х — из характеристик неделимого члена — Константы а и б) также зависят. §76 ATOM V E L E K T R I H E S K O M P O L E 353 2. Определить разделение уровня дублета (спин S = 1/2) Свободное (не слабое) электрическое поле.
Если размер раздела решения не мал по сравнению с Расстояние между компонентами дублета, возмущение от электричества Необходимо учитывать взаимодействие спина и орбитали одновременно. Оператор возмущения является суммой 1 ^ 2 Г — £ <s V = A S L— £ {a + 2b2 I (См. (72.4) и предыдущий выпуск). Удалить важность разделения Константа, перепишите этот оператор в следующем виде (см. (29.11)) V = J [, S + L_ + S-L ++ 2SzLz] до b £ 2L2z.
Для каждого данного значения M = M j собственное значение Оператор th определяется корнем светского уравнения. Количество матричных элементов для состояния | M l M s) = = | M 1/2, ± 1/2). Используя уравнение (27.12) <M-1 / 2,1 / 2 \ V \ M-1 / 2,1 / 2} = | (m-i) -b £ 2 (m- ^), 2 (M + 1/2, -1/2 \ V \ M + 1/2, -1/2) = -j [M + M-b £ 2 \ M + ^ (М-1/2, 1/2 \ V \ M + 1/2, -1/2} = j 1/2
В результате сдвиг уровня (см. Вопрос 1 в 39) A E = -b £ 2M 2 ± (l + i) + b £ 2 (b £ 2 + A) M 2; (1) Все условия здесь опущены. То же самое для всех компонентов Гусиный дублет. Это выражение (оба символа перед маршрутом) \ M \ ^ L-1/2 для всех уровней. Значение \ M \ = L-1/2 1 состояние | M l M s), и сдвиг уровня просто задается Диагональный матричный элемент.
Тот же выбор добавки Как константа и (1) D E = (| + ^) (£ + 1) — ^ (1 + 1) ‘(2) (Это соответствует результат, полученный по уравнению (1) с одним знаком Перед маршрутом). 3. Определить квадрупольное расщепление уровня с помощью осевого моделирования. Измеритель электрического поля 1).
В поле, симметричном относительно оси Z решения, d2tp d2r d2r = -m = a, m = -2a, дх до д з x) Аналогичная проблема для любого поля см. вопрос 6, §103 Оставшаяся вторая производная равна нулю. Квадрупольный оператор (76,8) В энергии есть форма + Q y y до 2Q z z) = 2 Дж (2 ^ _ (5 2-3 Дж!). Замените оператор своим собственным значением, чтобы получить смещение Уровень A E = a ——- ^ ——- [J (J + 1) — 2 J (2 J-1) V ‘J 4.
Рассчитать поляризуемость основного состояния атома водорода. Тензор поля вследствие сферической симметрии определяемого s-состояния Осуществимость сводится к скалярному (ACC = a8cc). Но (76,5) a = -2 e 2 Y k E 0-E k (Дипольный момент электрона dz = ez \ E q — энергия на уровне земли).
Вводит вспомогательный оператор b согласно определению _ ха дБ ч дт (Ха — масса электрона). Тогда zok = (i m / h 2) (Eo-Ek) bok и 2im e 2g 2 ime2 ^ 2, Z0hbkO = 2 (zb) 0 0- (1) P2 Vk fi Чтобы рассчитать эту сумму, достаточно знать результат действия b. Волновая функция pho (r). Согласно (9.2) = 1- ^ Φb-b n) φ0. н д н н Выразим функцию b0 как b (r) Φ0 и учтем ее 6 = офофо, где = = -h2 A / 2 m + C / (r), 6 (r) производная уравнение (1/2) phoAb + V & Vt / ´o = gff.
Перестановка b = cos Of (r) (6 — полярный угол сферической координаты natach, z = r cos c) сводится к следующему виду G + £ 2 г г2 Решение должно удовлетворять конечному условию fφo при r О IG 4 (X). В основном состоянии атома водорода φ0 = exp (-r / ac) / y / a (o, b = = ft2 / me2 — радиус Бора).
Решение уравнения (2), удовлетворяющее Условия настройки включают / = —1r av (av + r / 2). Из уравнения (1) 1) сейчас 2 б / 2 /} \ у „ч 9 с OL = — (r / cos 6 «) oo = — (rf) oo = -ac. И £ 6а х) В следующем разделе вы найдете этот результат по-другому. § 77 А ТОМ В О Д О Р О Д А В Е Л Е К Т Р И Ч Е С К О М П О Л Е 355 5.
Рассчитать поляризуемость электронов на границе S-состояние в потенциальной яме с радиусом действия силы. И x ca 1 при расчете элементов матрицы решений Ment (ZB) ® игнорировать область в яме и может быть использован во всех Пространственная волновая функция Ф.О.
Относится к области вне ямы (эта функция нормализации также учитывается Условие k a <C 1; см. §133 для этого. Предыдущее уравнение (2) Задача принимает форму И решение, удовлетворяющее граничному условию: / = —r2 / 2 x. вы Результаты получены путем количественного определения на основе уравнения (1). Te 2 OL = -m-g. 4H2 до 4
Смотрите также:
| Рентгеновские термы | Атом водорода в электрическом поле |
| Мультипольные моменты | Электронные термы двухатомной молекулы |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

