Смещения вдоль линий на плоскости

Оглавление:

Смещения вдоль линий на плоскости.

Смещение по линии i на плоскости. «Действительное число» x, о котором мы говорили в предыдущих двух главах, можно рассматривать со многих точек зрения, но его также можно рассматривать как число без какого-либо геометрического значения. Его можно рассматривать тремя различными способами: мера длины, то есть длина A0P вдоль линии A из главы I. Его можно рассматривать как значок с точкой x от A0, то есть значок с точкой I. Смещение рассматривается как мера или изменение положения в строке А. Сосредоточьтесь на этой третьей перспективе.

Смещение или изменение положения, необходимое для перемещения частицы из R в Q, называется смещением PQ. Чтобы полностью определить смещение, нам нужны три элемента данных: его размер, его ориентация по прямой и точка приложения, называемая начальной позицией P частицы. Однако, когда речь идет только об изменениях положения, вызванных смещением, естественно рассматривать все смещения с одинаковой длиной и одинаковым направлением как эквивалентные без учета точки приложения.

Представьте себе маленькую частицу в точке P на линии A и перейдите к Q. Людмила Фирмаль

Далее смещение полностью определяется длиной PQ = x, а его ориентация определяется знаком x. Таким образом, мы можем описать смещение [l:] и написать PQ— (\ x). Используйте квадратные скобки, чтобы отличить смещение [dg] от длины или числа l: 2). а является координатой [Мы показываем отношения AT: AB, AR: AD по воздуху соответственно. ~ AT-препарат, ~ AR ~ $ AD, AU = aAB + AD, AS-AB-fp AD. Пересеките RU с AC в точке P. Поскольку точки R, U и P коллинеарны *), AP = -) — AR-f-III. Где q / X — отношение, которое P делит RU. Другими словами Х + р. X + H- Однако P находится в динамике, поэтому AP = k AC = kAB — {- k AD, Где k — это конкретное число. В результате (пример 5) ac = pX + H1- ~ L Y1) Где вы пришли к выводу Симметрия полученного выражения показывает, что подобные аргументы должны приводить к отношениям Когда это пересечение. 19 Показания TS и AC. так Точки P и P ‘совпадают. ] 7. Пусть ABCD — параллелограмм, а M — середина AB. MD указывает, что динамик делится на соотношение 1: 3, а динамик делит MD на то же соотношение 1)

Умножение смещения. До сих пор не было предпринято никаких попыток придать смысл понятию произведения двух смещений. Единственное рассматриваемое умножение — это смещение и умножение чисел. выражение [X, y \ /] Это еще ничего не значит и может быть определено по желанию. Выбор определения определяется следующими принципами: Во-первых, ясно, что произведение двух смещений также должно быть смещением. Далее определяется [x, y > где a — действительное число Число, такое как [al:, ay], однако, a можно считать смещением [a, 0].

Решение задач по высшей математике

Плоские кривые	Комплексные числа
Геометрические места в пространстве	Геометрическое толкование умножения на i

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

Поэтому, изменив обозначение, во-вторых, благодаря определению, [, 0] [ ‘, /] = [XX1, xU), Наконец, в-третьих, наше определение должно следовать обычным правилам умножения, то есть переносимости, дистрибутивности и комбинации. [xy] [x, y \ = [x, y] [x, y], (! , y] + [x, y]) \ x «, y) = [x:, v] [x», y «1 + [x \ y] IX», Y], [x, Y] <[ ‘, y’J + [* «, Y]) [x, y] [x1, y] + [l- , Y) \ x «, Y | и [, y 1 ([l- ‘, y’] [x», Y ) = ([[x, y \ [x \ y ‘])] [ «, y «) Итак, [x> y] [* ‘> y’ \ = \ xx \ yy ‘] Это не правильное определение. [x, 0J [x ‘, y’ \ = [xx’y 0], Это противоречит второму требованию. 38. Следующие соображения приводят к необходимым определениям. Если OAB и OCD — это два одинаковых треугольника с равными углами вершин, вы можете видеть, что это O, A и C, а также B и D соответственно. OV OR OA —OS Или OB • OS = OA • OD (рисунок 20). Это пытается определить умножение и деление смещения, W- = £ ••, OB • OS = OA • OD. ОА ОС Давай OB = [x, y] 9 OS = [x’9 y ‘], OD = [X, Y). Поскольку A — точка (1,0), OA = [1,0]. тогда m-OD = [\, 0] [X, Y] = [X, VI Таким образом, \ x, y] \ x \ y ‘] = [X, Y].

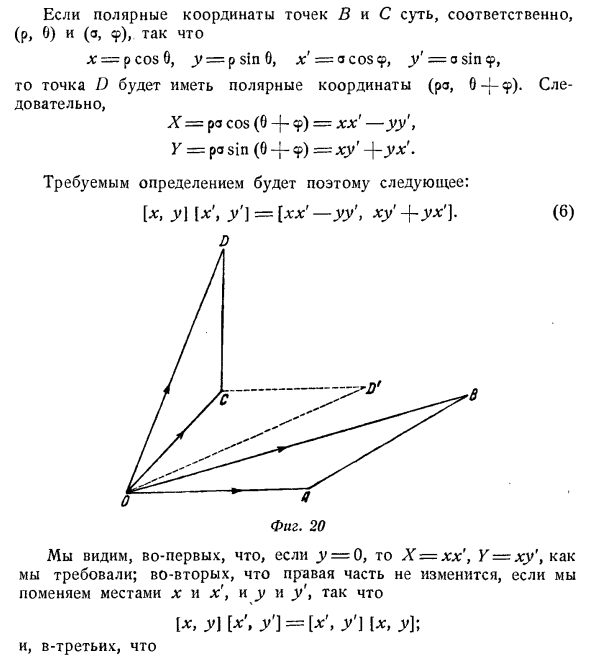
Следовательно, OB продукта должен быть определен как 01). Где точка I) получается путем построения треугольника, подобного треугольнику OAB в ОС. Обратите внимание, что ОС может создать два треугольника, OCD и OCD, чтобы устранить неоднозначность этого определения (см. Рисунок 20). Эти два треугольника похожи, и можно сказать, что они обращены в одном направлении.

Выбор угла COD, равного углу AO B, — это не только размер, но и знак. Людмила Фирмаль

Если полярные координаты точек B и C равны (p, 0) и (o, 9) соответственно, x = p cos 0, <y = psin0, x = o cos 9, y ‘= o sin 9 Затем точка I) имеет полярные координаты (pa, O-j-9). так X = pa cos (0 -f 9) = -yy ‘, Y = pa sin (0 -p 9) = xy — \ — yy (6) Следовательно, требуемое определение: [x, y \ x \ y ‘] = [lg:’ —yy \ xy ‘+ yh’]. D Во-первых, если y = 0, отобразите X = xx, Y-xy \ в соответствии с запросом. Во-вторых, замена x и x \ и y и y \ не меняет правую сторону, [x, y \ y ‘] = [x \ y’] \ x, y]; И в-третьих, это {[> Y \ + [ ‘. Y nix «, f ‘] = [* + ‘, y + y ‘] [x», y «\ — = [(x + x’) x» — (y + y ‘) y, {x + x ‘) Y «+ (y + y’) x» = = [xx «~ yy», xy «- {- yy»] -f- [x’x «-yy, x’y + y ‘x»} = = [> y] [x «, Y ‘] + [x \ Y] [x», y «]. Точно так же определение (6) удовлетворяет всем требованиям, представленным в разделе 37, поскольку можно подтвердить, что все отношения, указанные в конце раздела 37, выполнены.

Пример. Из приведенного выше геометрического определения, прямо покажите, что умножение смещения подчиняется закону ареста и распределения. [Например, рассмотрим закон перемещения. Продукт OB-OS — OD ^ cm. Та же фигура. 20) Кроме того, ХПК похож на AOB. Чтобы построить продукт OS-OB, необходимо построить треугольный BODt на OB, как с AOS. Следовательно, вам нужно только доказать, что точки D и Dx совпадают или что треугольник BOD и AOC схожи. Однако это простая задача для базовой геометрии. ]

Для точки P9 координата Q является a-f-lg. Поэтому смещение [π] перемещает частицу из точки a в точку a-} в x. Далее рассмотрим смещение на плоскости. Вы можете определить смещение PQ так же, как описано выше. Однако для полной установки смещения требуется больше данных. 1) величина смещения, т.е. длина сегмента PQ, 2) направление смещения, определяемое углом между PQ и неподвижной линией на плоскости, (3) направление смещения и (4) точка приложения согласования

Может отклонить это последнее требование Два смещения одинакового размера, одного направления и одинакового значения считаются эквивалентными. Если другой слон, PQ и RS равны и параллельны, и значение движения от P к Q такое же, как и движение от R к S, смещение PQ и RS считается эквивалентным, Та же фигура. 17 PQ-RS. Затем используйте плоскую систему координат (например, OX, OY и т. Д. На рисунке 17). Нарисуйте отрезок OL, равный и параллельный PQ, чтобы смысл перемещения от O к A был следующим: То же, что от P до Q. PQ и OA являются эквивалентными смещениями. Пусть x и y — координаты A. И очевидно, что если x и y заданы, OA полностью определено. ОА называется смещением [x, y J ol = p <s == yes == 1l:, Y) — 35. Смещение эквивалентно. Умножьте смещение на число. Очевидно, что если ξ и yj — координаты точки, а y и y — координаты точки Q x = V — 6, y = r / -r.

Таким образом, сдвиг от (S, tj) к (£ ‘, tj’) Ясно, что два смещения [x, y], [x \ y ‘\ эквивалентны, только если x = x’, y = y. Следовательно, если [x, y] = [x \ y ‘] • * == * ‘, y = ^ y \ (1) QP с обратным смещением — [& -r \ -r }>. R-— — VI = —G ^ ‘-ээ V —Ь ~ QP = -PQ. Эти отношения на самом деле являются определениями букв -S, tj ‘-tj] и -PQ. Ставь вот так — [*, *> —Y Естественно, дальше с этим согласен <* [*, Y] = \ * x, cty], (2) Где a — действительное число (положительное или отрицательное). Так, например, если OA OB == (см. Рисунок 17), Уравнения (1) и (2) определяют первые две важные концепции, связанные со смещением: равенство смещения и смещение, умноженное на число. 36. Добавление смещения.

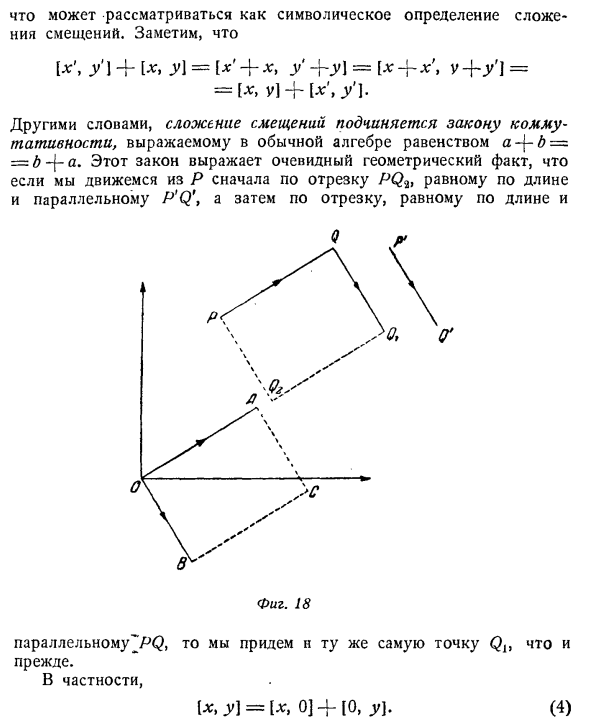
Мы еще не определили выражение. PQ + PV ‘, lx, yl + l x \ y’] Это имеет конкретное значение. Интуиция сразу говорит нам, что сумма двух смещений должна быть определена как смещение, возникающее в результате последовательной реализации двух данных смещений. Другими словами, QQ {если длина равна и параллельна P’Q ‘, то в результате непрерывного смещения PQ, P’Q’ частица сначала пойдет из точки P в точку Q, а затем в Qlt P’Q при передаче PQ и PQQ, таким образом рисуя OA, равную по длине и параллельную PQf и OB, OA, равную по длине и параллельную P’Q ‘, и завершая параллелограмм OASB,

(Рисунок 18). Рассмотрим результат этого определения. Если x \ y ‘является координатой точки B, координата центра отрезка AB 2 «(x 4» x ‘)> «2 (Y ~ LY)» и «Таким образом, координаты C * + Y- \ ~ Y ‘* Поэтому [*. Y] + 1x ‘, Y’) = [x + x \ y + y’1 (3) Это можно рассматривать как дополнительное символическое определение смещения. Пожалуйста, обратите внимание [x \ Y1 + [. Y \ = [x ‘+ x, y-hyj = [x- \ ~ x \ y + y’] = = [> vl-Hx \ y ‘). Другими словами, сложение смещения следует закону коммутативности, выражаемому в обычной алгебре уравнением a — \ — b = b-j-a. Этот закон при движении от P сначала движется по отрезку PQ2, который равен по длине и параллелен P’Q \, затем движется по отрезку, равному по длине, Та же фигура. 18 ^ Параллельно с PQ, достигните той же точки Q, что и раньше. особенно (4) [x, y] = \ xr, 0j + [0, y).

Где \ x> 0) означает смещение на расстояние x в направлении, параллельном OX. Это смещение указывается как 1 * 1 при рассмотрении только смещения по прямой линии. Компоненты [x, 0J и [0, \ x, y], а также вызов [x, y \ result]. После определения сложения двух смещений более нетрудно определить сумму любого количества смещений.

Если P, Q, R — три точки на одной прямой, то есть три действительных числа a, p, f, а не все ноль, OP-b p OQ -f для Wi равен 0. Обратное также верно. [Это просто парафраз примера 2. ] 5. A B и AC — два смещения не на одной прямой, а aAB + fAC = z tAB + SAC, Тогда =? и [Взять ABj = a ~ AB, AC1 = pAC. Завершите параллелограмм АВуРуСх. Тогда ARCH = aAB AC. Очевидно, что APX может быть выражен в этой форме только одним способом, и теорема продолжается. 6. Сделайте ABCD параллелограммом. Сегменты RQS и TQU проведены параллельно сторонам через точку Q внутри параллелограмма. Показывает, что RU и TS пересекаются в переменном токе (рисунок 19).