Оглавление:





Геометрические места в пространстве
- Геометрическое место в пространстве. В трехмерном пространстве существуют два принципиально разных класса геометрических мест, простейшими примерами которых являются плоскости и прямые линии. Существует только одна степень свободы для движения по прямой линии. Его направление движения фиксировано, и его положение может быть полностью определено с помощью одного измерения. Например, расстояние от фиксированной точки с линией. При приобретении прямой линии Ch от главной линии A. I, положение этой точки определяется единственной координатой x.
Чтобы исправить это положение, вам нужно определить две координаты. Геометрическое положение, представленное одним уравнением у) т Очевидно, относится ко второму классу рассматриваемых геометрических мест, называемых поверхностью. Это не всегда соответствует концепции нормальной поверхности. Соображения в пункте 31 могут быть четко обобщены, чтобы привести к определению функции f (x: y, z) трех переменных (или функции любого числа переменных).
Однако точки, которые движутся в плоскости, уже имеют две степени свободы. Людмила Фирмаль
И начал принимать, как было решено в §32, принять f (x, y) = 0 в качестве общего вида уравнения плоской кривой. f (x, y, z) = 0 Об общем виде уравнения поверхности. Геометрические места, представленные двумя уравнениями вида zf (x% y) или / (xt y, z) = 0, относятся к первому классу геометрических мест и называются кривыми , Таким образом, прямая линия может быть представлена двумя уравнениями: Ax -f-. CzD = 0. Круг в пространстве можно рассматривать как пересечение сферы и плоскости, поэтому он может быть представлен двумя уравнениями + (Ar ^ p-spi, Ax + By + Cz + D = * 0.
Пример XIX. 1. Что представлено тремя уравнениями вида f (x, y, z) = 0? 2. Обычно три линейных уравнения представляют одну точку * Что является исключительным случаем? 3. Каково уравнение плоской кривой f (x, y) = 0 в плоскости XOY, если рассматривать ее как кривую в пространстве? [f (x, y) = 0, z-0. ] 4. Цилиндр. Что означает одно уравнение f (x, y) => 0, которое рассматривается как геометрическое расположение точки в трехмерном пространстве? [Каждая точка на поверхности удовлетворяет уравнению f (x, y) = 0 независимо от значения z. Кривые от f (x, y) до 0, z-0 — это кривые, где геометрическое положение пересекает плоскость XOY.
| Функции двух переменных и их графическое представление | Смещения вдоль линий на плоскости |
| Плоские кривые | Комплексные числа |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Предпочтительным геометрическим положением является поверхность, образованная прямой линией, проведенной параллельно OZ, которая проходит через все точки этой кривой. Такая поверхность называется цилиндром. ] 5. Графическое изображение без плоскости на плоскости. Может оказаться невозможным получить достаточно точное изображение поверхности плана этажа. Тем не менее, очень четкое представление о природе поверхности может быть получено следующим образом: Пусть уравнение поверхности Z — f (xt y).
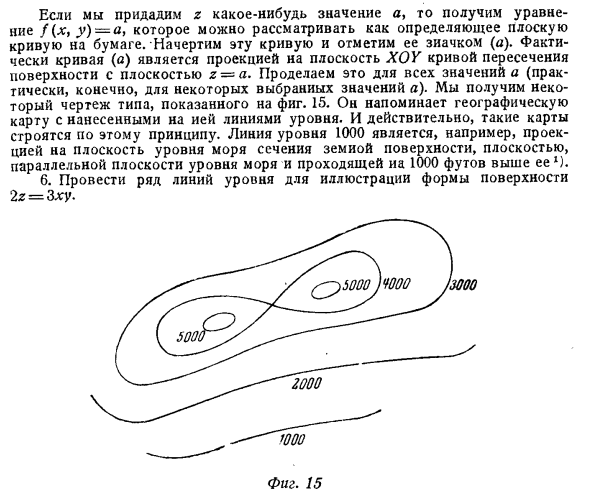
Это можно рассматривать как определение плоской кривой на бумаге. Нарисуйте эту кривую и отметьте ее символом (а). Фактически кривая (а) представляет собой проекцию пересечения поверхности и плоскости z на плоскость XQY. Это сделано для всех значений a (конечно, для некоторых из выбранных значений a). Получите чертеж типа, показанного на фиг. 15. Похоже на географическую карту с горизонтальными линиями.
Если вы дадите z значение, вы получите уравнение f (x, y) = a. Людмила Фирмаль
На самом деле такие карты построены по этому принципу. Горизонтальная линия 1000 представляет собой, например, проекцию участка поверхности Земли на поверхность моря, плоскость, параллельную поверхности моря и проходящую над ней на 1000 футов *). 6. Нарисуйте серию линий уровня, чтобы показать форму поверхности 2z = Zhu. Та же фигура. 15
Прямой конус. Получить начало вершины конуса и оси Z этой оси. Пусть a будет углом сечения конуса. Уравнение коники (которое предполагается продолжить по обе стороны вершины) принимает вид: + tg * ~ = 0. 8. Общее вращение поверхности. Конус в Примере 7 пересекает плоскость ZOX с двумя прямыми, соединенными уравнением xt = zitg2-rr. Это означает, что поверхностное уравнение было сформировано но Кривая y = 0, x * = z2
Вращением tg2 вокруг оси z вторая Заменив x1 в этих уравнениях на x2 + y2. В общем, указывает, что форма уравнения поверхности, образованной вращением вокруг оси zy кривой y-0, x-j (z), равна _ jAr’-b y * = / <*) • 9. Общий конус. Поверхность, образованная прямой линией через неподвижную точку, называется конусом, а эта точка называется вершиной конуса. Частным случаем является прямой конус, обсуждаемый в примере 7. Конические уравнения с вершинами Формат точки 0 — / (z / xt z / y) -0, и каждое уравнение этой формы представляет собой конус. [Если точка (x, y, z) находится на конусе, точка (Xx, Xv, \ z) также должна быть выше ее для значения X. ] 10. Линейная поверхность.
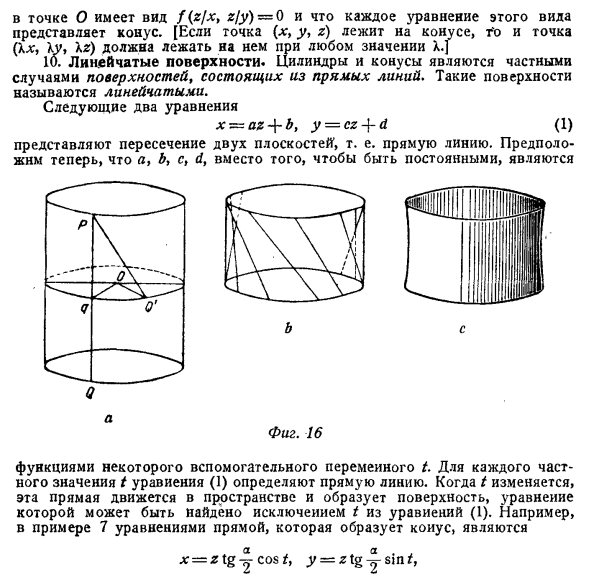
Цилиндры и конусы — это особые случаи поверхностей, состоящих из прямых линий. Такая поверхность называется линейкой. Следующие два уравнения x = az — {- b, y = cz -} — d (1) Та же фигура. 16 Q но Функция некоторых вспомогательных переменных t. Определите прямую линию для каждого конкретного значения / уравнения (1). При изменении t эта линия перемещается в пространстве, образуя поверхность, где уравнение можно найти, исключив t из уравнения (1). Например, в Примере 7 уравнение для линии, которая формирует коиус, имеет вид: X-Zlgicost, y = zzlg ^ -s \ nt, Где t — угол между плоскостью XOZ и плоскостью, проходящей через линию и ось z.
Другой простой пример линейчатой поверхности может быть построен следующим образом: Возьмите два отрезка прямого цилиндра, перпендикулярного оси и отстоящих друг от друга на расстояние / (рис. 16а). Вы можете представить себе цилиндрическую поверхность, состоящую из множества тонких параллельных жестких стержней длины / типа PQ. Концы этих стержней прикреплены к двум кольцам радиуса а. Затем прикрепите третье кольцо того же радиуса к цилиндру, чтобы расстояние было «/!» (От одного из первых двух колец (Рис. 16e, Pq = h). Угол P qOQ ‘-изображения a определяется из следующего соотношения, так что точка Q может быть зафиксирована на третьем кольце в положении Q’ Поверните все стержни, которые составляют цилиндр, таким же образом и под тем же углом. Мы получаем поверхность, форма которой является доминирующей

