Оглавление:






Уравнение Томаса-Ферми
- Уравнение Томаса-Ферми Численный расчет заряда и распределения электрического поля в атоме Метод свободного поля очень большой, особенно Сложность сложных атомов. Но просто сложный атом Существует метод аппроксимации от mov, и его значение Его простота Правда, это приводит к важным вещам Тем не менее, результаты, которые являются менее точными, чем последовательные методы Поле.
- Основа этого метода (Э. Ферми, Л. Томас, 1927) В сложных атомах с большим количеством электронов. Большинство электронов относительно велики Основное квантовое число. Поэтому мы можем применить Состояние отдельных электронов в атоме, понятие «клетка» В фазовом пространстве «(§48). Объем фазового пространства, соответствующий электро Импульс меньше р, Объем физического элемента dV равен -irp ^ dV. 3 322 ATOM GL X Этот объем соответствует ^ ячейки1).
Применимо в этих условиях Квазиклассическое приближение. Людмила Фирмаль
Это возможно Состояние, которое не может быть в нескольких состояниях одновременно 2 d V = ^ d V Z (2tg) 3 Ztg2 Электроны (по два электрона в каждой ячейке) Противоположный спин). В нормальном состоянии Элек Трон каждого элемента объема d V является Заполните соответствующую ячейку (в фазовом пространстве) Импульс от нуля до максимального значения p $. После этого кинетическая энергия электронов становится каждой Точка как можно меньше.
Если ты пишешь Чис Количество электронов в объеме d V, n d V, где n — числовая плотность E), то можно утверждать, что максимум Увеличение импульса электрона в каждой точке связь A _ = p. Ztg2 Максимальная кинетическая энергия электронов Поэтому места, где электронная плотность равна n, равны пирог = — (Ztr 2n) 2/3. (70,1) Кроме того, пусть p (r) — электростатический потенциал, Принимает ноль на бесконечности.
Общая энергия Электроны р 2 / 2- (с. Очевидно, полная энергия каждого Электрон должен быть отрицательным. в противном случае Электрон движется бесконечно. Указывает максимальное значение — (P $, где рассчитывается полная энергия электронов в каждой точке sro является положительной константой (это значение В некоторых случаях электроны переходят из меньшей средней точки К большой (по) точке.
Так что вы можете написать f = > — > o- (70.2) Если уравнения (70.1) и (70.2) выровнены, n = [2 (^ — ^ 0)] 3/2 ^ (70,3) -Отношение между электронной плотностью и потенциалом Аль во всех точках атома. х) В этом разделе используются атомные единицы. § 70U РА В Н Е Н И Е Т О М А С А-Ф Е Р М И 323 ip = (если p0, плотность n исчезает; n Очевидно, установлен на ноль для всего региона. Где Получить уравнение x1.21? = х 3/2 <Ш 7>
Граничное условие% = 1 при x = 0 и% = 0 при x = a Это уравнение больше не содержит параметров, Следовательно, общая функция x (x). В таблице. 2 Эта функция получается путем численного интегрирования Формула (70,7). х) Нормальная единица: Ze fr Z 1/3 м е 2 ‘ >> {? ) = -X ( гг V 0,885 В ч Функция x (x) монотонно убывает, исчезает только 1) бесконечный.
- Другими словами, в модели Томаса Ферми Атомы не имеют границ, но формально распространяются бесконечно Ерунда. Значение производной x ‘(x) AT x = O равно x7 (0) = = -1,59. Таким образом, для x -Y 0 функция x (x) имеет вид% <1-1,59 г. Следовательно, потенциал cp (g): <p (r) и Z / r-1.80 • Z 4/3. (70,8) Таблица 2 Значение функции Первый член — это ядерный потенциал, а второй — это потенциал.
Замена (70,6) (70.3) находит выражение для электронной плотности в следующем виде: Модель Томаса-Ферми показывает распределение плотов. Заряд разных атомов одинаков, x) Точное решение x (x) -144zh_3 уравнения (70.7), обратное От бесконечности до нуля, но не удовлетворяет следующим граничным условиям х = 0 Может использоваться как асимптотик Выражение функции x (x) для больших x.
Создано электроном происхождения. Людмила Фирмаль
Однако более или менее точный Эта формула дает значения только для очень больших х, м На больших расстояниях уравнение Томаса-Ферми обычно Сменный (см. Ниже). § 70U RA V N E N I E T O M A S A -F E R M I 325 Роль характеристического параметра длины — Z x / 3. (Обычная единица: H2 / (эти 2 Z x / 3), то есть делится на Z 1/3 bo Радиус робский).
При измерении расстояния в атомных единицах Заку, тогда, особенно расстояние электронных плотов Максимальное значение одинаково для всех Z. Таким образом, Большинство электронов в атоме Major Z находится на расстоянии порядка величины от ядра Z -1/3. В расчете половина полных электронов Атомный заряд находится в сфере с радиусом 1,33 Z -1/3.
Аналогичное соображение заключается в том, что средняя скорость Электронная плотность в атоме (учитывая по порядку) Порядок Z 2/3 как порядок, квадратный корень энергии). Уравнение Томаса Ферми Расстояние от ядра слишком мало или слишком далеко. Диапазон применения малых значений Корона (49.12); на меньшем расстоянии от подвесного поля Ядро является неуместным квазиклассическим приближением.
Предполагая a = Z в (49.12), нижняя граница Квазиклассическое приближение расстояния величиной 1 / Z сто Даже для больших r это не подходит для сложных атомов. Другими словами, для r ~ 1, длина волны де Бройля Электрон имеет порядок размера этого расстояния Чтобы полностью нарушить квазиклассические условия. Это можно проверить, оценив член в уравнении (70.2). (70.4), однако, результаты ясны заранее без расчета.
Это потому, что уравнение (70.4) не содержит Z. Следовательно, применимость уравнения Томаса Ферми Ограничено расстоянием более 1 / Z И меньше 1. Однако в этом сложном атоме Эта область содержит большинство электронов. Последняя ситуация является «внешней границей» Атомы в модели Томаса-Ферми находятся в г ~ 1, то есть в размерности Атом не зависит от Z.
Вместе с ними оказывается независимым Внешняя электронная энергия или потенциал Атомная ионизация 1). Вы можете рассчитать пол, используя метод Томаса-Ферми Энергия ионизации E, то есть энергия, необходимая для удаления Слияние всех электронов с нейтральными атомами. Сделать это х) Конечно, эта модель не отражает периодическую зависимость размера Периодически появляются атомы из Z и их потенциал ионизации. Элементная система.
Кроме того, было найдено эмпирическое доказательство Небольшое систематическое увеличение присутствия и размера Уменьшение потенциала ионизации с ростом атомов и Z. Рассчитать электростатическое распределение энергии Томаса Ферми с зарядом в атоме. Общая требуемая энергия равна Половина этой электростатической энергии в системе Частицы, взаимодействующие по закону Кулона, средняя кинетическая Энергия равна (по теореме вириала -I, см. §10) минус.
Половина средней потенциальной энергии. Зависимость E от Z проста Рассмотрение: электростатическая энергия Z электронов в электрическом поле Ядра с зарядом Z расположены на среднем расстоянии Z -1/3 от Ядро пропорционально Z • Z / Z -1/3 = Z 7/3. Численный расчет Привести к результату: E = 20,8 Z 7/3 эВ. Зависимость от Z хорошо согласуется с экспериментом.
Ментальные данные, опыт является фактором Это близко к 16. Я уже говорил положительные вещи, кроме нуля Значение константы (p $ соответствует ионизованному атому. При определении функции% с помощью cp- (po = Z x / r, около x Предыдущее уравнение (70.7) получено. Но мы должны быть заинтересованы Создать решение, которое исчезает, а не бесконечно, Нейтральный атом и конечное значение х = Такое решение существует в xq.
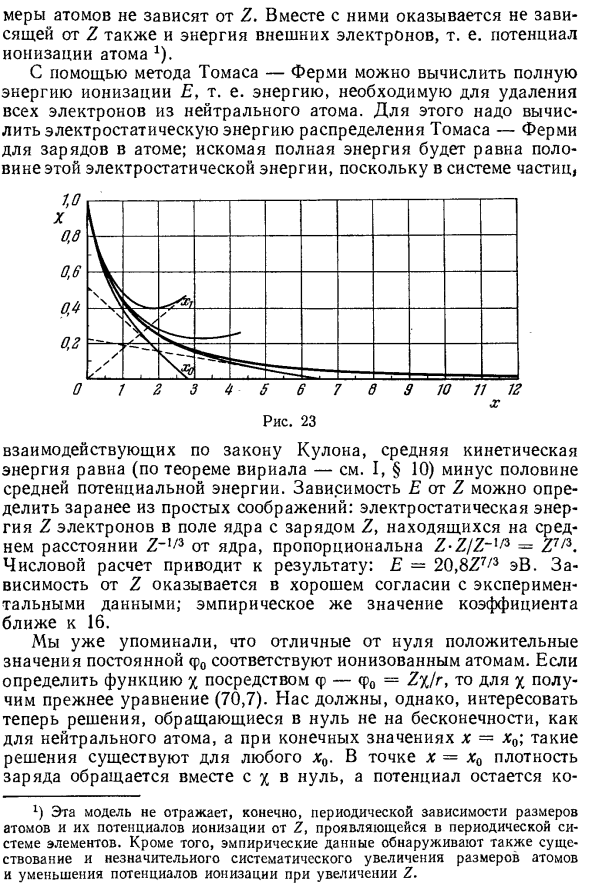
Плот в точке x = xq Значение заряда исчезает с x, но потенциал остается Финал. Значение x $ связано со степенью ионизации следующим образом Zome. Согласно теореме Гаусса полный заряд в сфере радиуса r Если сюда вставить x = xq, то определяется полный заряд иона z. Поскольку х (хо) = 0, Рисунок 23 Толстая линия показывает кривую х-х (х) Нейтральный атом Персональная степень ионизации.
Графически нарисованный Z / Z Длина отрезка отрезана от оси ординат касательной к кри Как далеко в x = xq. Формула (70.7) имеет решение, которое не поддерживает ни Место к нулю. На неопределенный срок эти решения расходятся. Они могут Считается, что соответствует отрицательным значениям Константа (fQ. На том же рисунке 23 показаны две такие кривые. X = x (x), они проходят через кривую нейтрального атома.
в Точка х = Х \, где равных Z х о ‘(Джо). (70.10) X f a) -x ix ‘ix i) = 0, (70.11) § 70U РА В Н Е Н И Е Т О М А С А-Ф Е Р М И 327 Общий заряд х <х \, содержащийся в сфере, обращен Ноль (графически эта точка явно Тангенс кривой проходит через начало координат). о В этот момент вы можете разорвать кривую и сказать, что он решает При плотности em x (x) граница нейтрального атома Заряд остается ненулевым. Физически это соответствует Это как «суженный» атом, окруженный определенной частью Окончательный том 1).
Рисунок 23 Уравнение Томаса Ферми не учитывает обмен Действие между электронами. Связанные эффекты-Next Следующий размер Z -2/3. Поэтому бухгалтерский обмен Взаимодействие с методом Томаса-Ферми требует одновременного Примите во внимание все эффекты этого порядка 2). Найти соотношение между энергией электростатического взаимодействия.
Энергия электронного взаимодействия и взаимодействия ядра Нейтральный атом модели Томаса-Ферми. Определить (потенциал поля, созданный электронами Вычтите из общего потенциала (p потенциал ядерного электрического поля Z / г. Энергия взаимодействия между электронами Uee = [<pend V = ^ j-dV- ^ (y n c v = 2 Дж г 4 Дж 1)
Эти соображения могут помочь вам рассмотреть следующую формулу: Состояние вещества при высокой степени сжатия. 2) Это А.С. Компанейц и Е.С. Павловский (Ж. Э. Ф. 1956. В. 31. С. 427) и Д. А. Киржниц (Ж. Э. Ф. 1957. Т. 32. С. 115). 328 ATOM GL. X (Выражается из ip в n согласно (70.3)).
Между тем, энергия Взаимодействия электронов с ядерным Уэном и их кинетическая энергия T равны RO U „= -z f 2 d v, T = =, J g J J 2 (2тг) 3 1 0 J Сравнение этих уравнений с предыдущим уравнением дает следующее соотношение: U — U — ТВ e e ^ ^ n -1- ■ 2 6 В то же время, согласно теореме Вириала (см. I, §10) При взаимодействии по закону Кулона 2 T = -U = -Uen-Uee- В результате Uee- ~ Uen *
Смотрите также:
| Водородоподобные уровни энергии | Волновые функции внешних электронов вблизи ядра |
| Самосогласованное поле | Тонкая структура атомных уровней |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

