Оглавление:



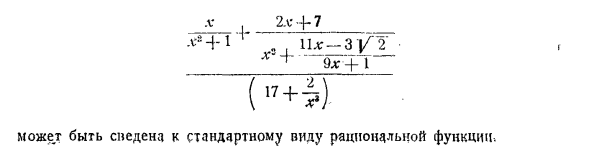
Рациональные функции
- . Разумная функция. Класс функций, которые следуют полиномам по простоте и важности, является классом рациональных функций. Рациональной функцией является отношение двух полиномов. Следовательно, если P (x) и Q (x) являются полиномами, Наиболее распространенная рациональная функция. В конкретном случае, когда Q (n 🙂 является константой, R (x) является полиномом. Следовательно, класс рациональных функций включает в себя класс полиномов в качестве подкласса.
(2) Однако следует отметить, что такие сокращения общих делителей обычно изменяют функциональность. Например, рассмотрим функцию х / х, которая является рациональной функцией. Уменьшение по общему коэффициенту x дает 1/1 = 1. Однако исходная функция не всегда равна 1. Только равен 1 для всех xzptO. Если π = 0, он принимает форму 0/0, что не имеет смысла. Следовательно, функция x / x равна 1, если η> 0, и не определена для η: = 0. Поэтому он отличается от функции 1, которая всегда равна 1. (3) и другие функции Можно привести к форме, согласно правилам алгебры а-8 (л: -2)
В связи с этим определением должны быть сделаны следующие утверждения: (1) В качестве общего правила предположим, что P (x) и Q (jc) не имеют общих делителей вида Сокращения. Людмила Фирмаль
Это представляет рациональную функцию в нормальном обозначении. Однако следует отметить, что это сокращение не всегда является законным. Чтобы вычислить значение функции для определенного значения x, это значение x должно быть присвоено функции формы>, где задано значение. В этом случае выражение, которое сначала определяет функцию, теряет свое значение для значений q = -1, 1, 0, 2, n. Следовательно, для 5 * этих значений не определена функция. Приведенная выше форма также теряет значение x = -1 и 1, но дает значение 0 для x = 0 и x = b, поэтому эти две функции снова не идентичны. (4) Однако, как мы уже видели из примера, рассмотренного в предыдущих замечаниях, в общем случае существует несколько наборов значений для x.
Рациональные функции не определяются даже после приведения к стандартной форме отношения двух полиномов. Это значения х, при которых знаменатель исчезает (которые могут не существовать). «(5) При работе с выражениями, рассмотренными в (2) и (3), разумной стандартной формой, обычно не обращающей внимания на исключительные значения x, где применяемый выше процесс алгебраического упрощения является незаконным
| Полярные координаты | Явные алгебраические функции |
| Дальнейшие примеры функций и их графическое представление | Неявные алгебраические функции |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Это предупреждение позволяет читателю легко подтвердить, что сумма, произведение и соотношение двух рациональных функций могут быть сведены к стандартной форме рациональных функций, которая в общем случае снова рациональна P (v) То есть, когда B7 = — ~, P (y) и Q (y) являются полиномами. v = Тогда после упрощения вы получите следующую форму: vi (x) ‘Wi (x) (6) При определении рациональных функций никогда не предполагается, что константы, встречающиеся в них как коэффициенты, должны быть рациональными числами.
: -Рациональные функции. Использование термина «разумный» произошло следующим образом: Рациональная функция tm-r может быть получена как конечное число Действие для х. Просто умножьте x на себя или на константу, добавьте полученные выражения и, наконец, разделите одну функцию, полученную в результате такого умножения и сложения, на другую. Для х этот процесс очень похож на процесс, где все рациональные числа могут быть получены из 1. Этот процесс можно объяснить равенством 5 _ 1 + 1 +1 + 1 -fl с ~ -1 + 1 + 1 С другой стороны, функции, которые могут быть получены из x посредством вышеуказанного действия, могут применяться к функциям, полученным таким же образом и сведенным к стандартной форме рациональных функций.
Термин «рациональный» относится только к тому, как переменная x включена в выражение, определяющее функцию. jgt-fx — \ — yb * y 2 —m Людмила Фирмаль
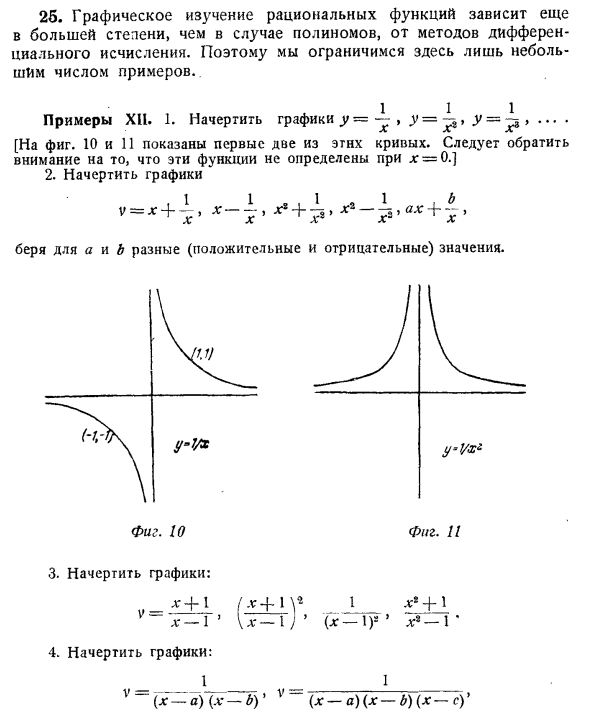
Например _ ‘9l: -f- 1__ («+ *) ■ Приведено к стандартной форме рациональных функций Исследование рациональных функций на основе графов больше опирается на метод дифференциальных вычислений, чем на полиномы. Поэтому мы ограничены несколькими примерами. Пример XII. 1. Нарисуйте график y-, d »= -, y = …. [Рисунок 2 Рисунки 10 и 11 показывают первые две из этих кривых. Следует отметить, что эти функции не определены для jc = 0. ] 2. Нарисуйте график * „-G D. 1 g 1 1 ** 1“ g b Принимает разные значения a и b (положительные и отрицательные). Та же фигура. Рисунок 10 и 3. Нарисуйте графику: o- £ ± I f- £ ± lV 1 _ f ‘+ J x-1 U-u ‘(x- \ y’ x * -1 4. Нарисуйте графику: v _ 1 _ ^ 1 (L: -a) (a * -b) ‘(X-a) (x-d) (x-cUГде а <б <в. 5. Нарисуйте формы кривых PR, которые больше и больше m, рассматривая нечетные и четные m случаев отдельно.

