Оглавление:



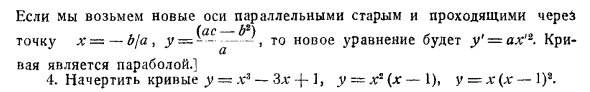
Дальнейшие примеры функций и их графическое представление
- Дальнейшие примеры функций и их графическое представление. Следующий пример дает читателю представление о бесконечном разнообразии возможных типов функциональности. А. Полином. Многочлен от x является функцией вида ^ ^ a ^ + … + d ^ Где a0, fl |, … f at — постоянные. Простейшим полиномом является y = x, xx, xm. График функции xm имеет вид Один из двух типов, в зависимости от того, является ли m нечетным или четным. Сначала рассмотрим случай m = 2.
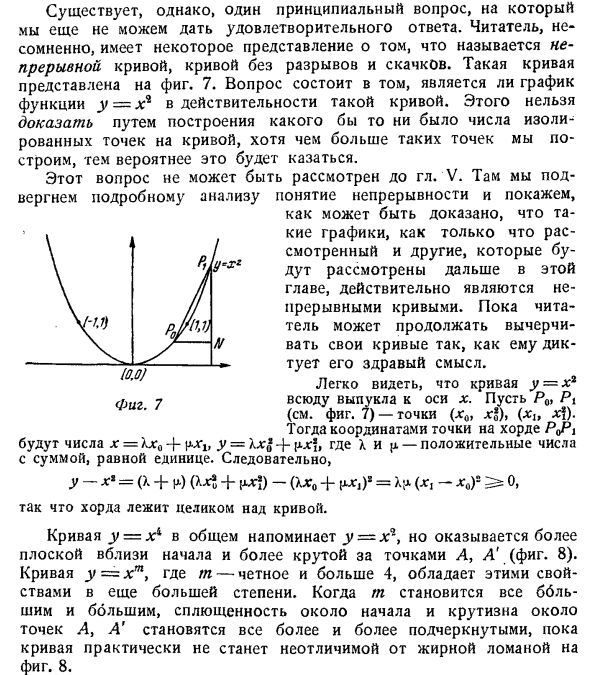
Так что ценность x ===: «2_» 2, 3, -fy, 2, 3 соответствуют значениям Y = T ‘4’ 9-7> 4> 9- Если читатель размещает на графике достаточное количество точек графика, делается вывод, что график должен иметь форму, показанную на фиг. 7. Если вы рисуете кривую через точку, которая, как вы знаете, находится на графике, и проверяете точность этой кривой, вычисляя новую точку, убедитесь, что она близка к кривой, как и ожидалось.
Далее на графике есть три точки: (0, 0), (1, 1), (–1, 1). * Указав частичное значение, вы можете найти любое количество других точек на графике. Людмила Фирмаль
Учитывая неизбежные неточности, связанные с рисунками. Конечно, эта кривая является параболой. ,Тем не менее, есть один фундаментальный вопрос, который все еще не дает достаточно ответов. Читатель определенно имеет представление о кривой без разрывов и скачков, называемой непрерывной кривой. Такая кривая показана на фиг. 7. Вопрос в том, является ли график функции y = x2 такой кривой. Это невозможно доказать, построив произвольное количество изолированных точек на кривой, но чем больше таких точек будет построено, тем выше вероятность этого.
Этот вопрос нельзя рассмотреть до гл. V. Детальный анализ и отображение концепции преемственности Как мы можем доказать, что график, который мы только что рассмотрели, и другие графики, приведенные далее в этой главе, на самом деле являются непрерывными кривыми? Пока читатель говорит ему, что здравый смысл подсказывает ему Вы можете продолжать рисовать кривую. Вы можете видеть, что кривая y = x2 всюду выпуклая относительно оси x.
| Графическое представление функций | Рациональные функции |
| Полярные координаты | Явные алгебраические функции |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
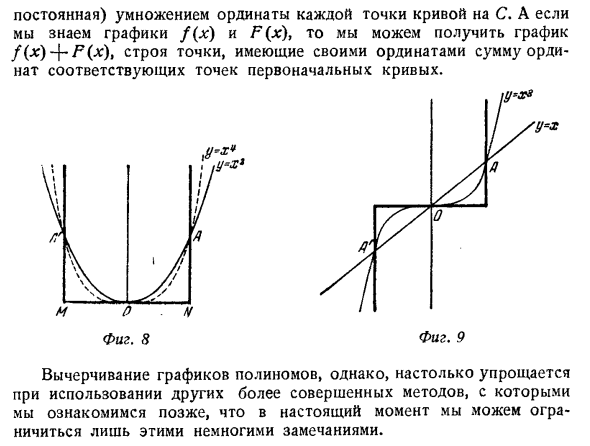
- Если P0 и Px (см. Рисунок 7) являются точками (x0, (x1, x1)), координатами точки в коде P0P1 являются числа x = \ xy-J- * * xit y = Xxf + jxxf, где X и q — положительные числа, а сумма равна 1. Следовательно, Y- = + u-) # + zx! ) — (X * 0 + = ^ — * o) 5 ^ o, Таким образом, код полностью на кривой. Кривая y = xi, как правило, похожа на _y = lg, но вы можете видеть, что начало более плоское и круто выходит за пределы точек A и A ‘(рисунок 8). Если кривая y = xy и m равно 4 или более, эти характеристики увеличиваются с увеличением rn до тех пор, пока толстая пунктирная линия и кривая на рисунке 8 не станут фактически неразличимыми, а точки A и A Крутизна в окрестностях все больше подчеркивается.
Где m нечетное число Основное различие между четным и нечетным состоит в том, что m является четным (-x) m = xm, поэтому кривая симметрична относительно Oy, тогда как m является нечетным (-x) m = -xm Х является отрицательным значением. Рисунок 1 Рисунок 9 показывает кривую y = xt y = x3 и пунктирную линию, которая y = xm подходит для больших нечетных значений m. Теперь легко представить (по крайней мере, в теории) построение полиномиального графа. Во-первых, сразу получаем график функций из графика y = xm
Далее читатель должен рассмотреть кривую, заданную уравнением y = xm. Людмила Фирмаль
Постоянная) Умножьте ординату каждой точки кривой на C. И если вы знаете графики f (x) и F (x), вы можете получить график / (■ *) + ^ C *), нанеся соответствующую сумму ординат на ординату Точка кривой. Та же фигура. Рис. 8 9 Однако построение полиномиальных графов значительно упрощается при использовании других более продвинутых методов. Это будет обсуждаться позже, но в настоящее время вы можете ограничиться этими комментариями.
Пример XI. 1. Нарисуйте кривую y = 7x * t y-Zdrg ‘, x = y10. [Читатель должен тщательно нарисовать эти кривые на одном рисунке М. Поскольку x увеличивается постепенно, порядок x увеличивается. x10 -f- Zlg5 -f- 7jc * (Или l: 10 -f-ЗОлг6700л: 4) Если x достаточно велико, только первый член имеет действительно доминирующее значение. Так, например, если l: равно 4, x1 *> 1 000 000, 30 ** <35 000 и 700 jc * <180 000, если l: = 10, превосходство первого слагаемого еще более важно , ] 2.Сравнить само значение L: 1 «, 1 000 000 L * 1 000 000 000 000 L: x = z 1, 10, 100 и т. д. (Читатель должен создать несколько примеров этого типа отдельно. Относительные скорости роста различных функций x часто описываются в следующих главах.) 3. Функция axxxc Создать график. (Нажмите здесь Взяв новую ось параллельно старой оси и пройдя точку x — b \ a, y = -a-, новое уравнение становится y ‘= aX. Кривая — это парабола. ] 4. Изогнутые y-x * -3x], y-l: 2 (x-I), y = x (x-I) 8.

