Линейная алгебра

Здравствуйте, на этой странице я собрала полный курс лекций по предмету «линейная алгебра»

Лекции подготовлены для школьников и студентов и охватывает полный курс предмета « линейная алгебра ».

В лекциях вы найдёте основные законы, теоремы, формулы и примеры задач с подробным решением.

Изучаемый в математике и рассматриваемый как единое целое объект, с которым производятся какие-либо математические действия, будем называть математическим объектом. К математическим объектам относятся, например, числа, геометрические объекты (линии, поверхности и т. п.), переменные величины и т. д.

Лине́йная а́лгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения[⇨], системы линейных уравнений[⇨], среди основных инструментов, используемых в линейной алгебре — определители, матрицы[⇨], сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры[1]. Такие объекты как квадратичные и билинейные формы[⇨], тензоры[⇨] и операции как тензорное произведение непосредственно вытекают из изучения линейных пространств, но как таковые относятся к полилинейной алгебре. wikipedia.org/wiki/Линейная_алгебра

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Линейная алгебра

Линейная алгебра — это раздел математики, касающийся линейных уравнений. Линейная алгебра занимает центральное место почти во всех областях математики. Например, линейная алгебра является фундаментальной в современных представлениях геометрии, в том числе для определения основных объектов, таких как линии, плоскости и вращения.

Кроме того, функциональный анализ, раздел математического анализа, можно рассматривать как в основном применение линейной алгебры к пространствам функций.

Линейная алгебра также используется в большинстве наук и областей техники , поскольку она позволяет моделировать многие природные явления и эффективно проводить вычисления с такими моделями. Для нелинейных систем, которые не могут быть смоделированы с линейной алгеброй, он часто используются для борьбы с аппроксимациями первого порядка, используя тот факт, что дифференциал из многомерной функции в точке является линейным отображением , что лучше аппроксимирует функцию вблизи этой точки.

Матрицы

Термин «матрица» был введен Дж. Сильвестром в 1850 году, в математику — А. Кэли в 1857 году. Матрицей называется математический объект, состоящий из 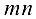элементов, взятых в определенном порядке.

Для указания на порядок элементов матрицы их выписывают в виде таблицы из 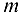строк и 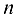столбцов. Элемент матрицы, стоящий на пересечении строки с номером 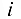и столбца с номером 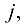обозначают 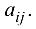Если 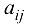— числа, матрица называется числовой. Обозначают матрицы большими латинскими буквами.
Обозначение матриц

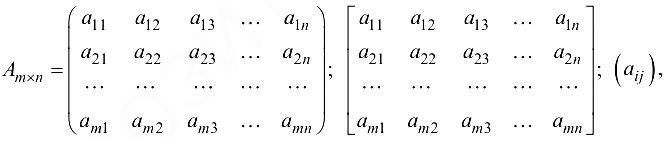
где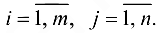

Иногда матрицу обозначают одной буквой, например,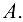

Основные виды матриц

Если число строк матрицы равно числу ее столбцов, т. е. 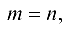то матрица называется квадратной. Порядком квадратной матрицы называется число ее строк (или столбцов). Строки и столбцы матрицы называют ее рядами.

Обозначение квадратной матрицы порядка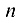

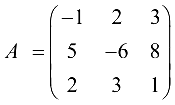— квадратная матрица 3-го порядка.

Две матрицы называются равными, если они имеют одинаковые размеры и элементы одной матрицы равны соответствующим элементам другой матрицы: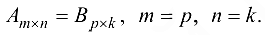

В квадратной матрице элементы 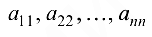образуют главную диагональ, а элементы 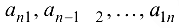— побочную.
Диагональной матрицей называется квадратная матрица, у которой отличны от нуля только элементы, стоящие по главной диагонали.

Диагональной матрицей называется квадратная матрица, у которой отличны от нуля только элементы, стоящие по главной диагонали.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной 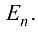Например,

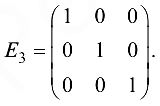Нулевой матрицей называется матрица, все элементы которой равны нулю: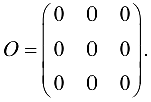

Симметрическая матрица — квадратная матрица, для которой 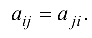Например, матрица 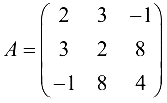симметрическая.

Трапециевидная матрица — матрица произвольных размеров, если она имеет вид

где 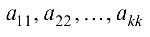отличны от нуля.

Треугольная матрица (частный случай трапециевидной) -квадратная матрица, все элементы которой по одну или другую сторону от главной диагонали равны нулю. Различают верхнюю и нижнюю треугольные матрицы. Например, матрица вида

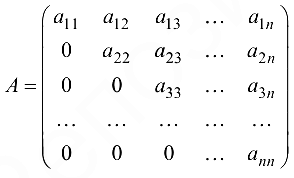называется верхней треугольной матрицей.

Матрица 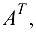полученная из данной матрицы 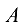заменой каждой ее строки столбцом с тем же номером, называется транспонированной к данной.

Если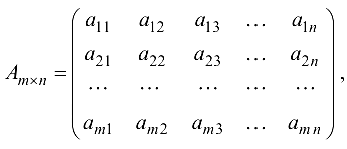

то

Операция нахождения матрицы, транспонированной к данной, называется транспонированием матрицы.
Матрица, состоящая из одной строки, называется матрицей-строкой. Она имеет вид 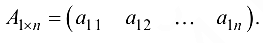Матрица, состоящая из одного столбца, называется матрицей-столбцом.

Имеет вид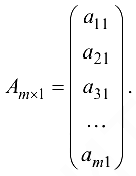

Действия над матрицами

К линейным операциям над матрицами относятся умножение матрицы на число, сложение матриц.

1. Умножение, матрицы на число.
   Произведением матрицы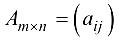 на действительное число
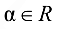   называется новая матрица 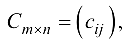где 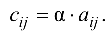Обозначение: 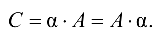Например,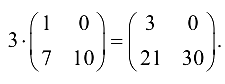
   

Матрица вида 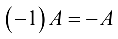называется матрицей, противоположной матрице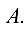

Сложение, матриц

Складывать можно только матрицы одинаковых размеров, т. е. имеющие одинаковое число строк и столбцов.

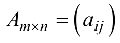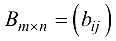Суммой двух матриц и называется матрица 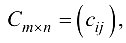где 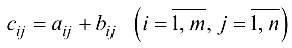и обозначается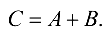

Пример №1.1.

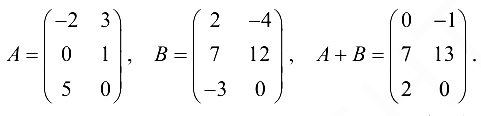
Разность матриц 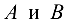определяется так: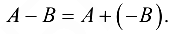

Умножение, матриц

Матрицу 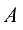будем называть согласованной с матрицей 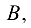если число столбцов матрицы 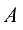равно числу строк матрицы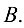

Пример №1.2.

Пусть

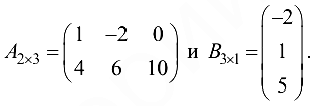
Матрица 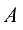согласована с матрицей 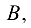но матрица 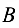не согласована с матрицей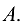

Если матрица 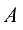согласована с матрицей 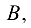то произведением матрицы 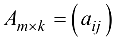на матрицу 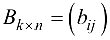называется новая матрица 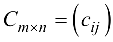такая, что

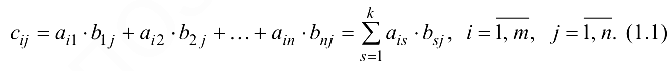
Формула (1.1) называется правилом произведения матриц.
Из определения произведения матриц следует, что для того, чтобы получить элемент произведения матриц 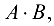стоящий в 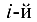строке и 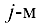столбце, нужно умножить элементы 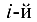строки матрицы на соответствующие элементы 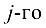столбца матрицы 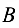и эти произведения сложить.

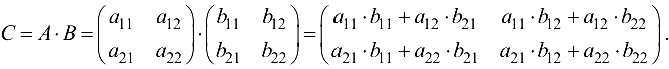
Пример №1.3.

Вычислить 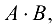если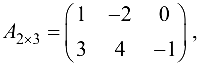

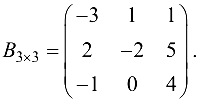
Решение:

Матрица 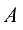(три столбца) согласована с матрицей 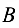(три строки).

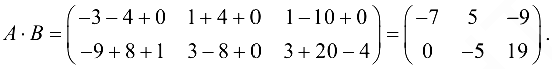
Замечание. Умножить матрицу 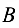на 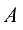в данном случае нельзя — число столбцов матрицы 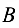(три) не равно числу строк матрицы 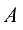(двум).

Замечание. Так как в общем случае 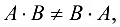то произведение матриц не коммутативно.

Свойства действий над матрицами

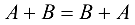(коммутативность относительно сложения).

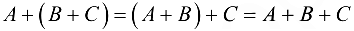(ассоциативность).

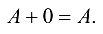
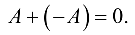
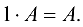
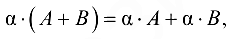где 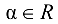(дистрибутивность сложения матриц относительно умножения на число).

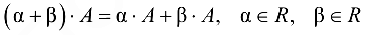(дистрибутивность сложения чисел относительно умножения на матрицу).

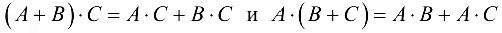(дистрибутивность умножения).

Транспонирование связано со сложением и умножением матриц нижепредставленными формулами.

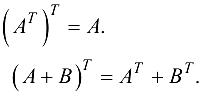
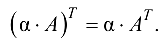
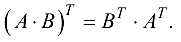
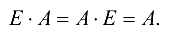
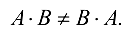
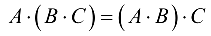(ассоциативность).

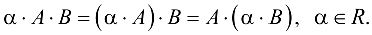
Доказательство этих формул вытекает непосредственно из определений соответствующих операций сложения и умножения.

Определители и их основные свойства

Понятие «определитель» было введено Г. Лейбницем и японским математиком Кова Секи независимо друг от друга в 1683 году.
Развитие теории определителей нашло свое отражение в работах Ю. Вронского, Э. Кристоффеля, О. Коши и Дж. Сильвестра.
Понятие определителя (детерминанта) матрицы вводится только для квадратной матрицы.

Дана квадратная матрица 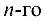порядка

Определитель 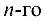порядка, порожденный матрицей 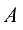порядка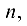

имеет вид

Определитель обозначается 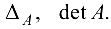Определитель является числовой характеристикой квадратной матрицы.

Элементы, строки, столбцы и диагонали матрицы называют соответственно элементами, строками, столбцами и диагоналями определителя матрицы.

Определителем матрицы первого порядка 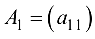называется сам элемент 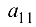этой матрицы. Обозначение: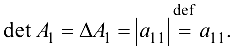

Определителем матрицы второго порядка 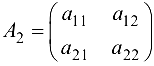называется число, равное разности произведений элементов главной и побочной диагоналей, т. е.

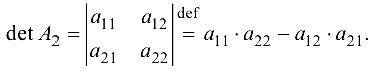
Пример №1.4.

Вычислить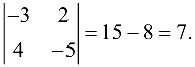

Определитель третьего порядка имеет вид

Элементы 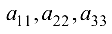стоят на главной диагонали, элементы 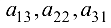— на побочной.

Существует ряд правил для вычисления определителей третьего порядка. Так, например, значение определителя третьего порядка можно вычислить по правилу треугольников:

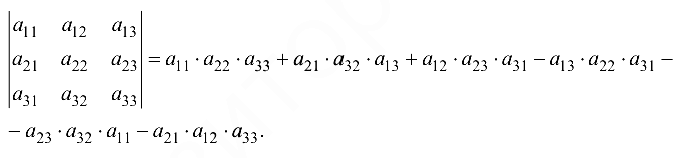
Можно вычислить также по правилу Саррюса: к определителю приписывают справа первый и второй столбцы.

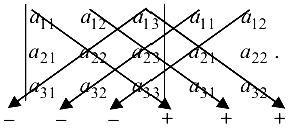
Произведения из трех элементов, стоящих на главной диагонали и на прямых, ей параллельных, берутся со знаком «+», а произведения из трех элементов, стоящих на побочной диагонали и на прямых, ей параллельных, берутся со знаком «-».

Пример №1.5.

Вычислить определитель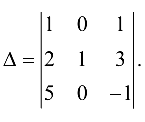

Решение:

Воспользуемся правилом треугольников:

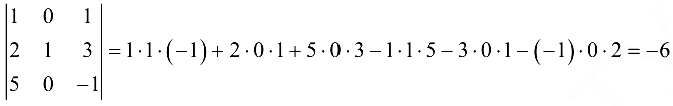
или по правилу Саррюса

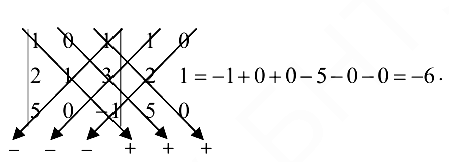
Определители четвертого и более высоких порядков при вычислении сводятся к определителям более низких порядков (например, третьего).

Основные свойства определителей

Иллюстрация этих свойств будет приведена для определителей третьего порядка.

1. Свойство инвариантности (неизменности) определителя при транспонировании матрицы: при замене строк столбцами величина определителя не меняется (причем каждую строку следует заменить столбцом с тем же номером). Свойство выражает равноправность строк и столбцов. В дальнейшем слова «строка» и «столбец» заменим одним словом — ряд. Свойство записывается так:

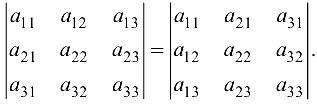
Доказательство. Проверим справедливость этого свойства, применяя правило треугольников к левой и правой части равенства (1.2) и сравним результаты:

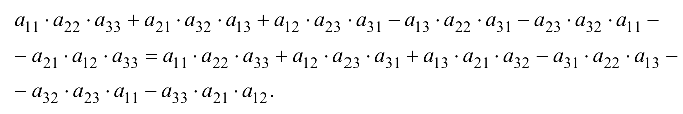
2. Если поменять местами два параллельных ряда, то определитель изменит знак.
Так, например, переставляя первый и второй столбцы, получаем

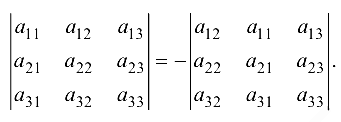
3. Если определитель имеет два одинаковых параллельных ряда, то он равен нулю.

4. Если в определителе элементы какого-либо ряда содержат общий множитель, то его можно вынести за знак определителя.

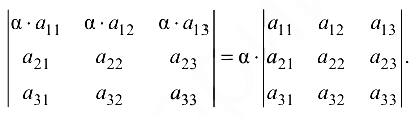
Следствие 1. При умножении определителя на скаляр (число) необходимо умножить на этот скаляр только один из рядов определителя.
Следствие 2. Величина определителя равна нулю, если элементы какого-либо его ряда равны пулю.

5. Определитель, у которого элементы двух параллельных рядов пропорциональны, равен нулю.

6. Определитель, у которого каждый элемент некоторого ряда является суммой двух слагаемых, равен сумме двух определителей, у первого из которых в указанном ряду стоят первые слагаемые, а у второго — вторые слагаемые. Остальные ряды, параллельные указанному, у всех определителей одинаковы.

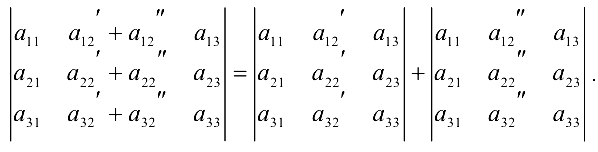
Все сформулированные свойства (2-6) доказываются аналогично первому, т. е. по правилу треугольников.
Минором 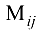элемента 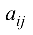называется определитель, который получается из данного путем вычеркивания строки с номером 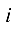и столбца с номером 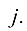Например, для элемента 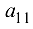минором является определитель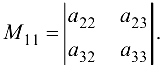

Алгебраическим дополнением 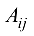для элемента 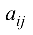называется его минор 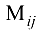, взятый со знаком 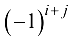, где 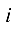— номер строки,
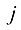— номер столбца. 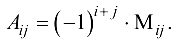Например, для элемента 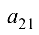алгебраическое дополнение имеет вид

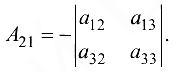
7. Теорема Лапласа. Определитель равен сумме произведений элементов любого ряда на соответствующие алгебраические дополнения элементов этого ряда.

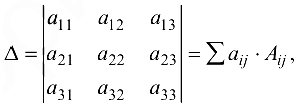
где

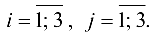
Доказательство. Докажем в случае разложения по элементам первого столбца.

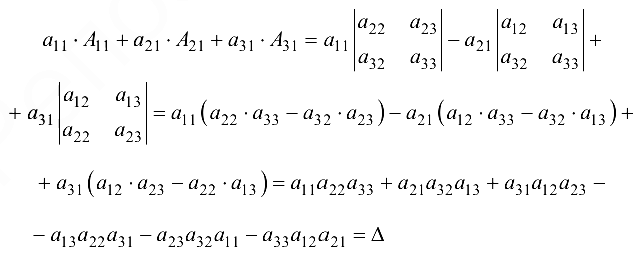
Пример №1.6.

Вычислить определитель 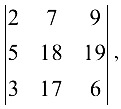разлагая по элементам второго столбца.

Решение:

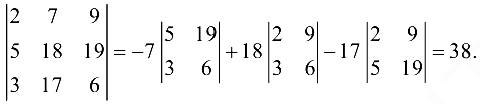
8. Величина определителя не изменится, если к элементам какого-либо ряда прибавить элементы другого параллельного ему ряда, предварительно умноженные на одно и то же число. Например, убедимся, что

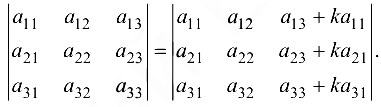
На основании свойства 6

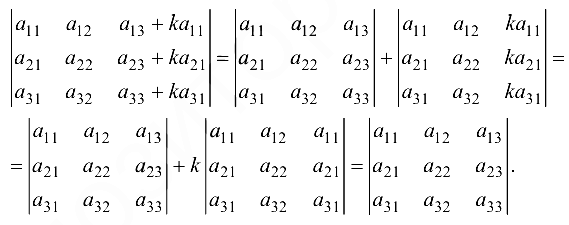
В этой сумме второй определитель по свойству 3 равен 0. Свойство 8 широко используется для получения пулей в определителе и приведения его к треугольному виду.

Пример №1.7.

Вычислить определитель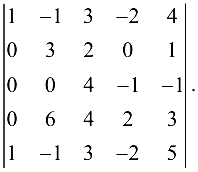

Решение:

Если из пятой строки вычесть первую, а из четвертой — удвоенную вторую, то полученный определитель

будет с нулями под главной диагональю, и он равен произведению элементов, стоящих на его главной диагонали,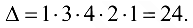

Пример №1.8.

Вычислить определитель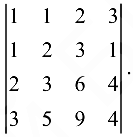

Решение:

Если из второй строки вычесть первую, из третьей -удвоенную первую, из четвертой — утроенную первую, то получим определитель 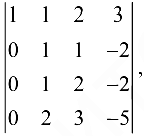равный исходному. Разложим полученный определитель по элементам первого столбца (используя свойство 7), и определитель примет вид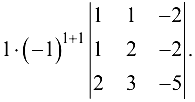

Используя свойство 8 можно записать 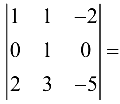по свойству 7

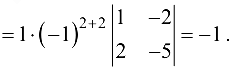
9. Теорема аннулирования. Сумма произведений элементов некоторого ряда определителя на алгебраические дополнения другого параллельного ему ряда равна нулю:

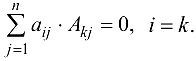
Доказательство. 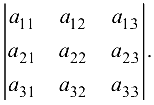Составим сумму произведений элементов первой строки на алгебраические дополнения элементов второй строки:

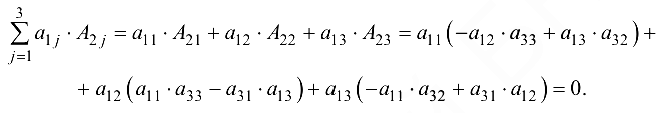
Свойства определителей широко используются при вычислении определителей произвольного порядка.

Определитель произведения квадратных матриц

Теорема. Определитель произведения двух квадратных матриц одного порядка равен произведению определителей этих матриц, т. е.

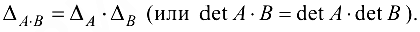
Доказательство теоремы проведем на примере матриц второго порядка.

Дано

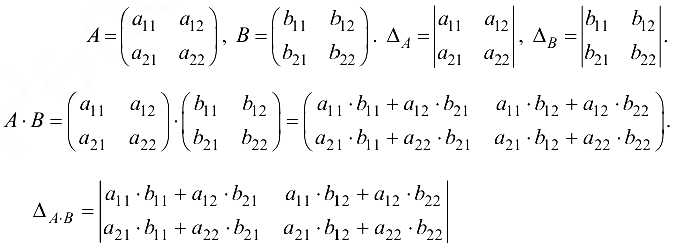
на основании свойства 6 определителей имеем

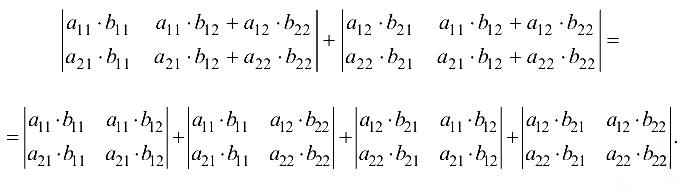
На основании свойства 4 запишем

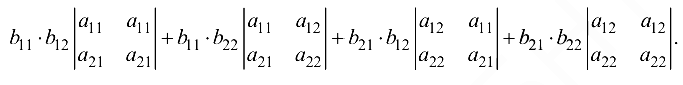
Первый и четвертый определители равны нулю на основании свойства 3:

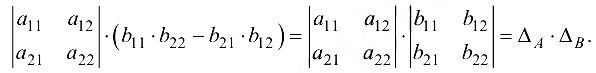
Аналогично эта теорема доказывается для квадратных матриц любого порядка.

Обратная матрица

Понятие обратной матрицы вводится только для квадратной матрицы. Квадратная матрица 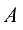называется невырожденной, если ее определитель не равен нулю, т. е. 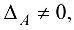и вырожденной, если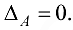
Матрица 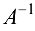называется обратной квадратной матрице 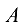, если

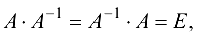
где 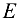— единичная матрица.

Союзной матрицей для квадратной матрицы

называется матрица

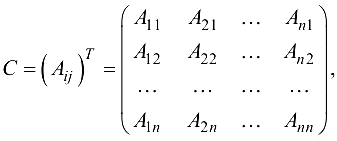
где 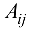— алгебраические дополнения к элементам 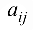матрицы 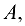где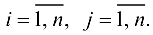
Лемма. Если 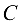— союзная матрица для матрицы 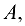то

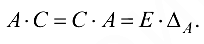
Теорема (о существовании обратной матрицы). Для того чтобы существовала матрица 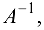обратная матрице 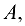необходимо и достаточно, чтобы матрица 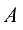была невырожденной.
Доказательство необходимости. Пусть для матрицы 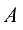существует обратная матрица 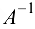. Докажем, что 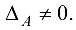Так как 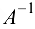существует, то на основании формул (1.6) и (1.7) следует:

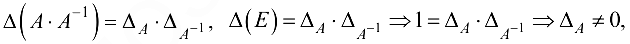
т. е. матрица 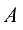невырожденная.

Доказательство достаточности

Пусть 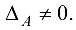Докажем, что 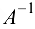существует.
Если 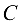— союзная матрица для матрицы 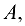то справедлива формула (1.9). Разделим равенство (1.9) на 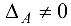и получим

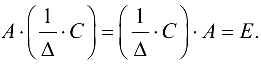
Из этого равенства на основании формулы (1.7) следует, что в качестве обратной матрицы выступает матрица

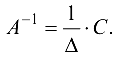
Замечание. Из доказательства достаточности следует правило нахождения обратной матрицы.

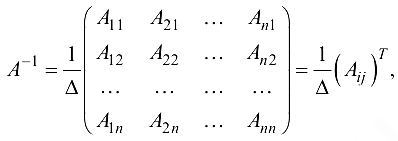
где 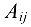— алгебраические дополнения элемента 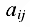матрицы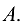
Свойства обратных матриц

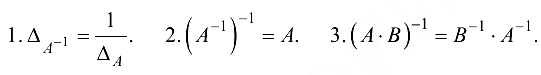
Правило для нахождения обратной матрицы

1. Вычислим определитель матрицы 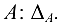Пусть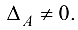

2. Найдем алгебраические дополнения для элементов .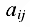
Составим матрицу алгебраических дополнений определителя 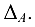Обозначим ее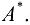

3. Полученную матрицу 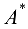транспонируем и обозначим ее 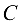(союзная матрица).

4. Союзную матрицу 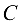умножим на 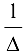и получим обратную
А
матрицу .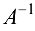

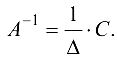
Пример №1.9.

Найти обратную матрицу матрице

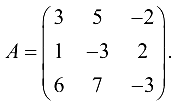
Решение:

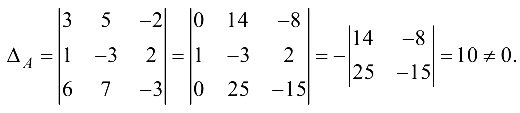
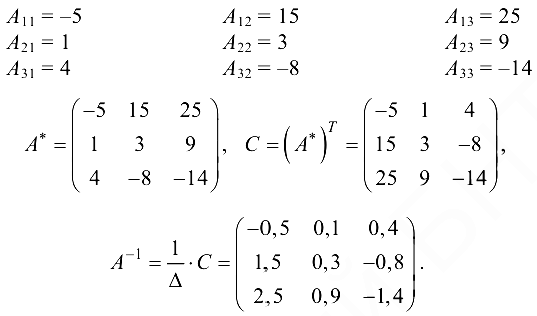
Теорема. Для невырожденной матрицы существует единственная обратная матрица.
Доказательство. Докажем методом от противного. Предложим, что для матрицы 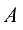существует две обратные матрицы 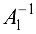и .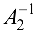

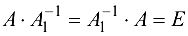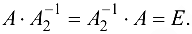По определению обратной матрицы имеем и или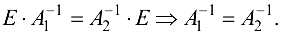

Системы линейных алгебраических уравнений. Матричная запись системы. Основные определения

Системой 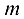линейных уравнений с 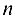неизвестными называется система вида

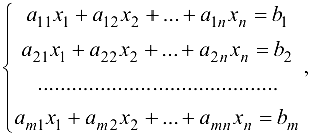
где 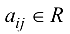— действительные числа, называемые коэффициентами системы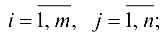

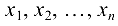— неизвестные системы; 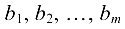— свободные члены системы.

Все неизвестные в первой степени, поэтому система (1.11)- это система линейных уравнений.
Если все свободные члены системы (1.11) равны нулю, то система называется однородной.

Матрица 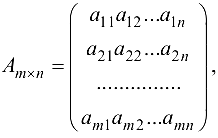составленная из коэффициентов системы, называется матрицей системы. Матрица 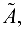полученная из матрицы 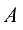добавлением столбца свободных членов, называется расширенной матрицей системы

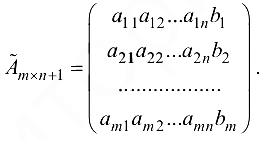
Если через 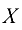обозначить матрицу-столбец из неизвестных, т. е.

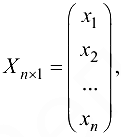а через 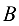— матрицу-столбец свободных членов, т. е. 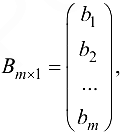то так как матрица 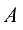(имеет 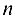столбцов) согласована с матрицей 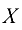(имеет 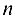строк), произведение 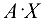существует и линейную систему (1.11) можно записать в матричном виде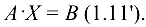

Упорядоченная совокупность чисел 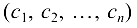называется решением системы (1.11), если каждое из уравнений (1.11) обращается в верное равенство после подстановки вместо 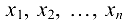соответственно чисел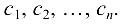

Решение системы, записанное в виде матрицы-столбца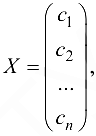

называется вектор-решением системы.

Если существует хотя бы одно решение системы (1.11), то она называется совместной, и несовместной, если она не имеет решений.

Совместная система называется определенной, если она имеет единственное решение.

Система, имеющая более одного решения, называется неопределенной.

Решить систему — это значит выяснить, совместна она или несовместна, и в случае совместности найти все ее решения.

Две системы называются эквивалентными или равносильными, если всякое решение одной из них является решением другой и наоборот.

Решение невырожденной системы линейных алгебраических уравнений матричным методом и по формулам Крамера

Габриель Крамер (1704-1752) — швейцарский математик, один из создателей линейной алгебры.
Рассмотрим систему 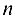линейных уравнений с 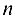неизвестными.

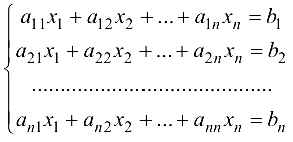
или

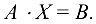
Определитель матрицы А имеет вид

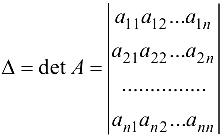
и называется определителем системы. Если 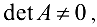то система называется невырожденной. Найдем решение системы, предполагая что 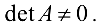В этом случае матрица 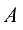невырожденная и для нее существует единственная обратная матрица (по теоремам пп. 1.1.6)

Умножим матричное уравнение (1.12′) слева на 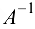и получим

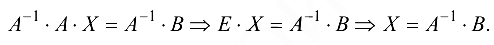
Формула (1.13)- решение системы (1.12) в матричном виде. Это равенство можно записать так:

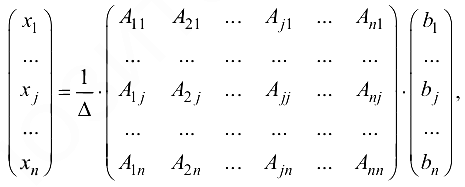
где 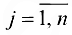или

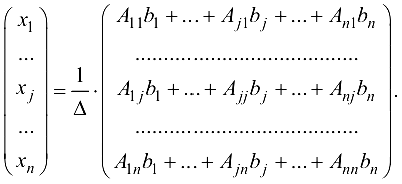
Из формулы (1.13′) видно, что любая переменная 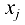определяется по формуле

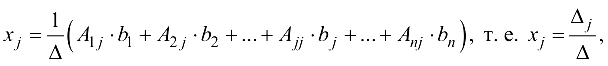
где 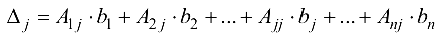— определитель, полученный из заменой 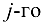столбца столбцом свободных членов. Формулы (1.14) называются формулами Крамера.

Пример №1.10.

Решить систему

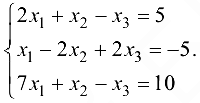
Решение:

Матрица 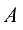имеет вид

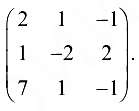
Вычислим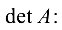

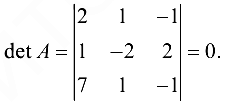
Следовательно, матрица вырождена и система несовместна, т. е. нет решений.

Пример №1.11.

Решить систему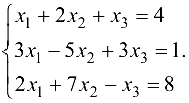

Решение:

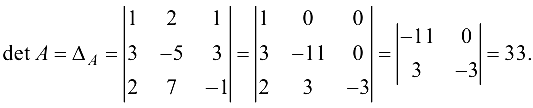
а) Так как 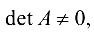то матрица 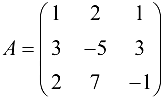невырожденная и решение системы найдем матричным методом, т. е. по формуле (1.13): 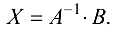Найдем обратную матрицу 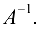Составим алгебраические дополнения:

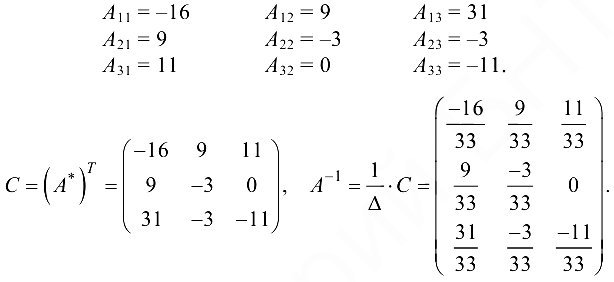
В данном случае матричное равенство (1.13) запишем в виде

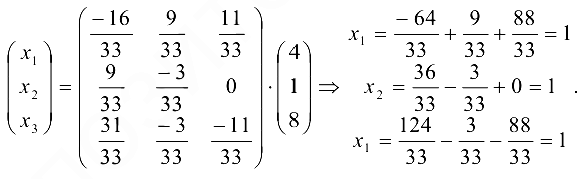
б) Решим данную систему по формулам Крамера (1.14):

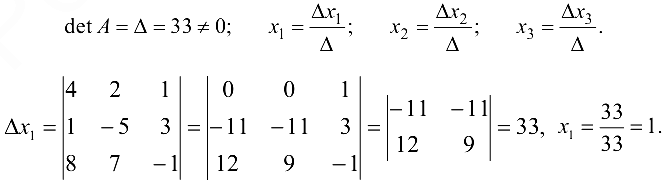
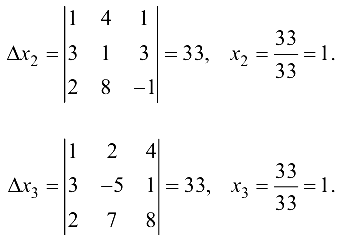
Ответ: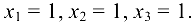

Ранг матрицы

Элементарные преобразования матрицы.

Рассмотрим матрицу 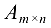и выделим в ней произвольно 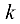строк и 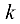столбцов:

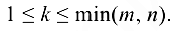
Определитель 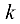-го порядка, составленный из элементов матрицы 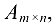стоящих на пересечении выделенных 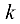строк и 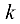столбцов, называется минором 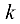-го порядка этой матрицы и обозначается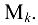

Рангом матрицы 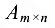называется наибольший из порядков ее миноров, отличных от нуля.
Ранг обозначается любым из символов: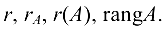

Из определения ранга следует:
1) для матрицы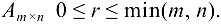

2) 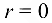тогда и только тогда, когда все элементы матрицы равны нулю;
3) для квадратной матрицы 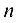-го порядка 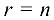тогда и только тогда, когда матрица невырожденная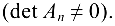

Отметим важное свойство миноров матрицы, которым пользуются при нахождении ранга.

Теорема 1. Если все миноры порядка 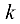данной матрицы равны нулю, то все миноры более высокого порядка равны нулю.
Доказательство этой теоремы следует из теоремы Лапласа (свойство 7).

Свойства ранга матрицы

1. Ранг матрицы, полученной изданной вычеркиванием какого-либо ряда, равен рангу данной матрицы или меньше его на 1.
2. Ранг матрицы, полученной из данной приписыванием к ней ряда, элементами которого являются произвольные числа, равен рангу исходной матрицы или больше его на 1.
3. Если вычеркнуть из матрицы или приписать к ней нулевой ряд, то ранг матрицы не изменится.
4. Ранг матрицы, полученной из данной транспонированием, равен рангу данной матрицы.

Ранг матрицы обычно находят:

• методом окаймляющих миноров (МОМ);
• методом элементарных преобразований (МЭП).
  Метод МОМ.
  Минор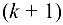 порядка матрицы 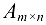называется окаймляющим для минора 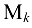, если он содержит все элементы 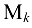(в любом порядке).
  Суть метода МОМ: если какой-нибудь минор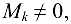 а все его окаймляющие миноры 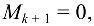то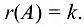

Пример №1.12.

Определить ранг матрицы

Решение:

Среди элементов матрицы 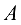есть не равные нулю, например, элемент, который находится в левом верхнем углу 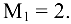Среди миноров второго порядка, которые окаймляют этот элемент, есть не равные нулю, например, 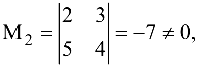следовательно, ранг матрицы равен 2 или больше. Вычисляем окаймляющие миноры для 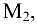например, 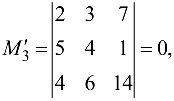но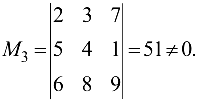

Следовательно, ранг матрицы равен 3 или больше, так как среди миноров третьего порядка есть отличный от нуля.

Вычисляем все окаймляющие миноры для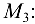

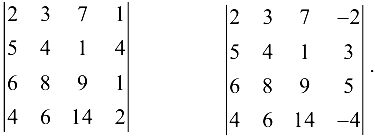
Все они равны нулю (четвертая строка пропорциональна первой), и поэтому ранг матрицы не равен четырем. Итак, ранг матрицы равен трем.

Метод МЭП

Рассмотрим метод нахождения ранга матрицы с помощью элементарных преобразований.

Элементарными преобразованиями матрицы называют:
1) умножение некоторого ряда матрицы на число, отличное от нуля;
2) прибавление к одному ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число;
3) перестановку местами двух параллельных рядов.
Если матрица получена из матрицы 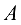с помощью элементарных преобразований, то матрицы 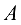и 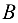называются эквивалентными, при этом пишут 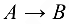(или ).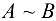
Теорема 2 (об инвариантности ранга). Ранг матрицы, полученной из данной элементарными преобразованиями, равен рангу данной матрицы, т. е. если 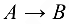, то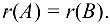
Суть МЭП состоит в том, что данная матрица 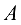с помощью элементарных преобразований сводится к эквивалентной матрице 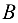трапециевидной (или треугольной) формы.

Тогда в силу теоремы 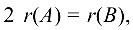а ранг трапециевидной матрицы 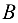равен числу ее ненулевых строк ( 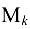в левом верхнем углу не равен пулю) и, таким образом,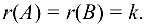

Пример №1.13.

Найти ранг матрицы

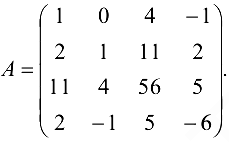
Решение:

С помощью элементарных преобразований сведем матрицу к трапециевидной:

Произвели следующие преобразования: ко второй строке матрицы 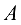прибавлена первая, умноженная на (-2); к третьей строке прибавлена первая, умноженная на (-11); из четвертой строки вычтена первая, умноженная на 2; из новой третьей строки вычтена новая вторая, умноженная на 4; к четвертой строке прибавлена вторая.

Полученная матрица 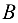имеет ранг равный 2, так как она трапециевидна и имеет две ненулевые строки, следовательно, и ранг матрицы 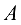равен двум.

Пример №1.14.

Найти ранг матрицы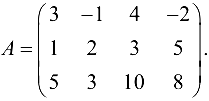

Решение:

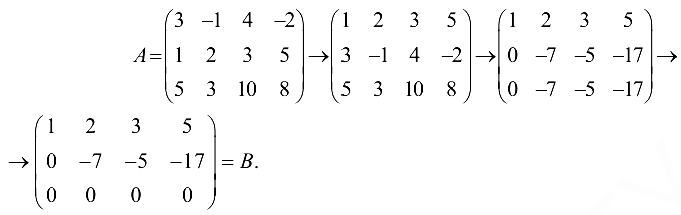
Матрица 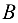имеет трапециевидную форму. Минор второго порядка этой матрицы, составленный из элементов первой и второй строк, не равен нулю: например,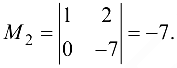

Следовательно, 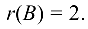По теореме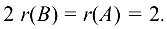

Итак,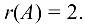

Пример №1.15.

Определить ранг матрицы

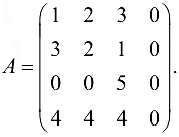
Решение:

С помощью элементарных преобразований приведем матрицу 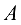к трапециевидной форме или треугольной. Вычеркнем столбец из нулей. А затем элементы первой строки матрицы умножим на -3, 4 и сложим соответственно с элементами второй и четвертой строки и получим

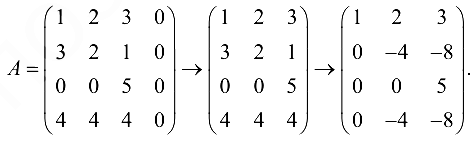
Из новой второй строки вычтем новую четвертую строку, четвертую строку вычеркнем и получим

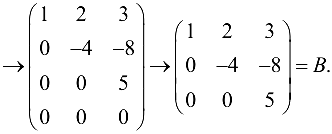
Минор третьего порядка матрицы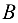

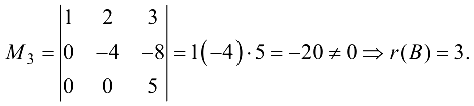
По теореме 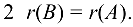Значит,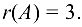

Базисным минором матрицы называется отличный от нуля ее минор, порядок которого равен рангу матрицы.

Например, для матрицы 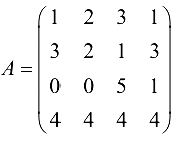базисный минор имеет вид

Для ненулевой матрицы существует не единственный базисный минор. Строки и столбцы, на пересечении которых стоят элементы базисного минора, называются базисными.

Если в матрице некоторый ряд может быть представлен в виде суммы 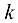других параллельных ему рядов, умноженных соответственно на числа 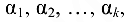то данный ряд является линейной комбинацией указанных рядов.

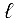параллельных рядов матрицы линейно зависимы, если хотя бы один из этих рядов является линейной комбинацией остальных. В противном случае параллельные ряды называются линейно независимыми.

Теорема (о базисном миноре). Любая строка (столбец) матрицы является линейной комбинацией базисных строк (столбцов). Базисные строки (столбцы) матрицы линейно независимы.

Теорема. Если ранг матрицы 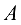равен 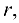то существует 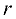линейно независимых строк (столбцов), от которых линейно зависят все остальные строки (столбцы).

Теорема (о связи ранга с независимостью рядов). Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов в этой же матрице и равно ее рангу.

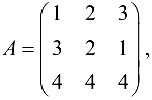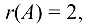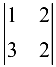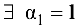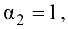Например, дана матрица ранг а один из базисных миноров размещается в первых двух строках. Это означает, что третья строка является линейной комбинацией первой и второй строки. Если и то

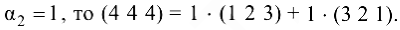
Решение произвольных систем
Теорема Кронекера-Капелли

Рассмотрим произвольную систему линейных алгебраических уравнений

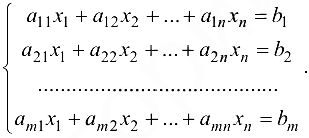
Число уравнений может быть и не равно числу неизвестных. Обозначим через матрицу данной системы, а через — матрицу, полученную из 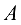присоединением столбца свободных членов:

Матрица 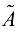называется расширенной матрицей системы.
Теорема Кронекера-Капелли (о совместности системы линейных уравнений). Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее матрицы 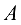равнялся рангу расширенной матрицы .

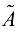Решение произвольных систем

Теорема. Если ранг матрицы 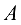равен рангу матрицы 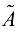и равен числу неизвестных, т. 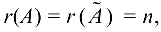е. где 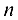— число неизвестных, то система имеет единственное решение.
Теорема. Если ранг матрицы 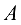равен рангу матрицы 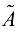, но меньше числа неизвестных, т. е. 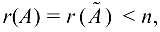то система имеет бесконечное множество различных решений.
Теорема. Если ранг матрицы 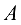не равен рангу матрицы 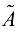, то система не имеет решений.

Базисными неизвестными совместной системы, ранг которой равен 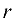, назовем 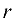неизвестных, коэффициенты при которых образуют базисный минор. Остальные неизвестные назовем свободными. Так как базисный минор может быть выбран не единственным образом, то и совокупность базисных неизвестных может быть выбрана не единственным образом.

Пример №1.16.

Исследовать на совместность и решить следующие системы уравнений:

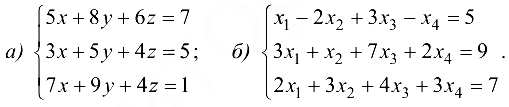
Решение:

а) Матрица системы имеет вид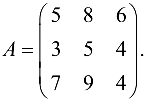

Преобразуем расширенную матрицу системы:

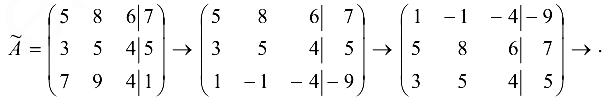
В матрице 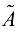из 3-й строки вычитаем удвоенную 2-ю и ставим полученную строку на 1-е место. Умножаем эту строку на -5, на -3 и складываем результаты соответственно со 2-й и 3-й строкой и получаем

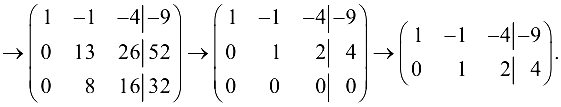
Так как миноры 2-го порядка, например, 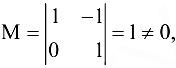то 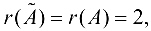следовательно, система совместна. Число неизвестных системы 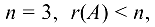то система имеет бесчисленное множество решений. В качестве базисного минора можно взять, например,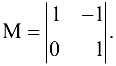

При таком выборе базисного минора базисными неизвестными будут 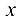и 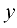, а свободным — .

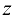Запишем систему в виде 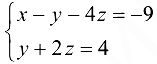или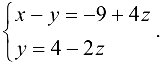

Полагая, что 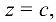по формулам Крамера получим

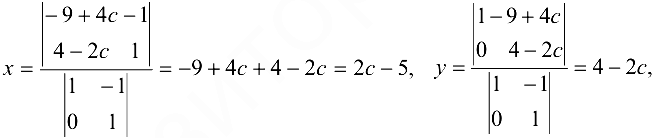
где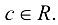

Ответ: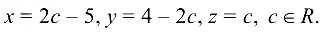

б) 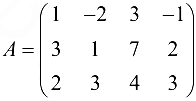— матрица системы.

Преобразуем расширенную матрицу, умножив первую строку на -3 и на -2 и сложив с соответствующими элементами второй и третьей строками:

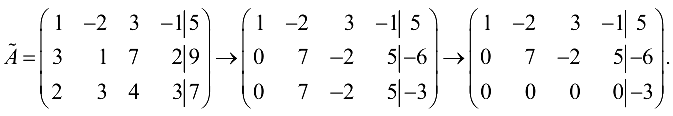
Так как 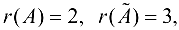то система несовместна.

Системы линейных однородных уравнений

Рассмотрим однородную систему линейных алгебраических уравнений

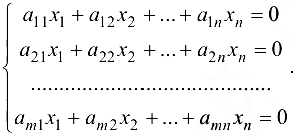
Система (1.15) является частным случаем системы (1.11). Однородная система (1.15) всегда совместна, так как ранг ее матрицы равен рангу расширенной матрицы.

Решение является решением системы (1.15), оно называется нулевым или тривиальным.
Однородная система имеет тривиальное решение тогда и только тогда, когда ранг матрицы системы равен числу неизвестных. В частности, когда 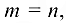то для того, чтобы система (1.15) имела только тривиальное решение, необходимо и достаточно, чтобы определитель системы был отличен от нуля.
Если ранг матрицы системы меньше числа неизвестных 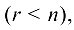то система (1.15) имеет бесчисленное множество решений и решается аналогично неоднородной произвольной системе.

Пример №1.17

Решить систему однородных уравнений

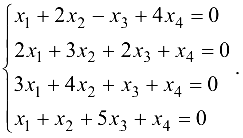
Решение:

Найдем ранг матрицы системы, преобразовав матрицу:

Так как ранг матрицы системы равен числу неизвестных, то однородная система имеет единственное нулевое решение.

Метод последовательного исключения неизвестных (метод Гаусса)

Дана система 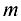уравнений с 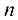неизвестными:

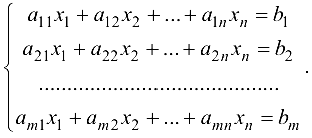
Для решения этой системы применим метод Гаусса, состоящий в последовательном исключении неизвестных.

С помощью элементарных преобразований над строками система 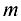линейных уравнений с 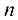неизвестными может быть приведена к трапециевидной форме:

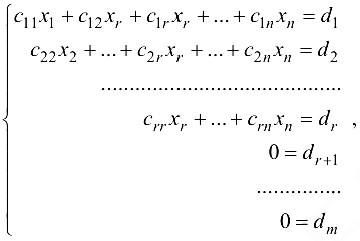
где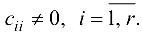
Система (1.16) эквивалентна исходной системе. Если хотя бы одно из чисел 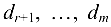отлично от нуля, то система (1.16), а следовательно, и исходная система несовместны. Если же 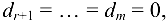то система совместна и из уравнений (1.16) выражают последовательно, начиная с последнего уравнения, находим последовательно значения неизвестны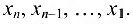

Пример №1.18.

Методом Гаусса решить систему

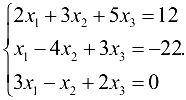
Решение:

Производя элементарные преобразования над строками расширенной матрицы, получим

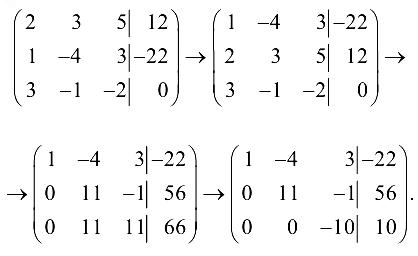
Этой матрице соответствует система

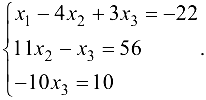
Решив эту систему, получим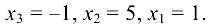
Ответ: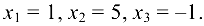

Пример №1.19.

Методом Гаусса решить систему

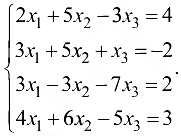
Решение:

С помощью элементарных преобразований над строками расширенную матрицу приведем к трапециевидной форме:

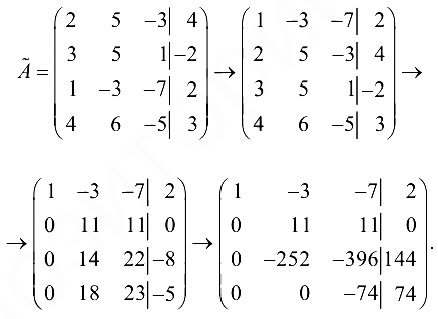
Этой матрице соответствует система

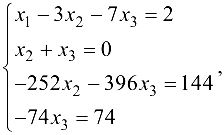
решив которую получим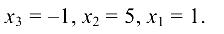

Пример №1.20.

Решить систему

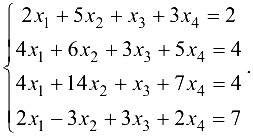
Решение:

Производя элементарные преобразования над строками расширенной матрицы получим.

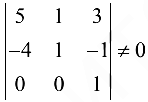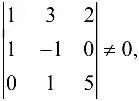Поскольку и то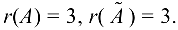

Этой матрице соответствует система

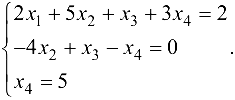
Так как ранги равны, т. 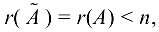е. где 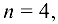то система имеет бесчисленное множество решений.
Данная система эквивалентна преобразованной системе.

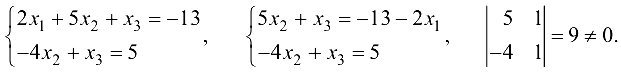
За базисные неизвестные примем 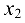и 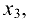свободная неизвестная будет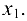

Полагая, что 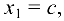решим систему по формулам Крамера:

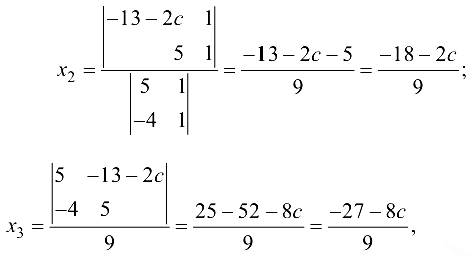
где 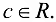Итак,

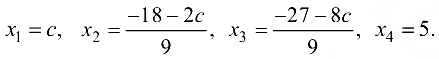
Придавая с различные числовые значения, будем получать различные решения данной системы уравнений.

Возможно эти страницы вам будут полезны:

• Решение задач по линейной алгебре
• Помощь с линейной алгеброй
• Заказать контрольную работу по линейной алгебре
• Заказать работу по линейной алгебре
• Теория из учебников тут
• Готовые контрольные работы по линейной алгебре