Оглавление:
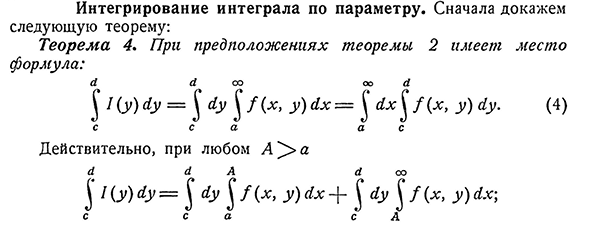



Интегрирование интеграла по параметру
- Интегралы интегралов по параметрам. Сначала докажем следующую теорему: теорема 4. В предположении теоремы 2 Формула: а=^а^с х)у = ^ г У^/(х,г) С С С С а Действительно, при^>а Л у А6? ООО Р(_y)г
г=4г^/(х,г)Ах -]~<1У Р(х, г) ых-, (4) 158ЧАП. Интегралы, зависящие от параметра [305] Но-по теореме 4Н°298-А-А-А-А-а§(1У§/е х=Г Г З§ / Л У,
з а с ы Так в чем же разница а а^1(г)ю-§г х^/г г С а с Она написана в виде Людмила Фирмаль
§/(г)s1u-§ю§/г х — § § s1u§ / ЛК.и если сейчас—сколь угодно малого е^>0-взять и большой, так、 ООО Один. Но Для всех y упомянутая разница (абсолютно) меньше, чем e (y—C). В этом деле、 а и7 (г)г г=11SH \ ЛК я/ю, И — * ОО ы ы Это эквивалентно(4). Используя теорему 3[n°304], легко
вывести такой результат отсюда. Для $(X, y), если одна непрерывность интеграла превышает(1) y, то требуется выражение(4). Таким образом, при определенных условиях устанавливается право на перестановку двух интегралов, один из которых распространяется на бесконечный интервал,а другой-на конечный Интеграл. С другой
- стороны, вам часто приходится сортировать интегралы по обоим бесконечным интервалам в соответствии с формулой 00ОО С а так что … Г Х=Y х^/(х,у) (1У. С (5) Часто бывает трудно и кропотливо обосновать такую перестановку. Только формула (5) для узкого класса случаев
может быть обоснована общими соображениями. Используя равномерную сходимость интеграла 159 Определите функцию теоремы 5 T (x, y) и сделайте X^A и Y последовательными. Далее, предположим, что оба интеграла н ы м и Н е п р е р ы функции, первая из y,следующую-Х. Девять. (6) Существует и другое, есть равенство (b). Предположим, что интеграл (6) существует во втором Интеграле. Согласно предыдущим результатам, для конечного
C^>C это выглядит так Ы ы ы ы ы ы ы Репортаж Джона Херсковица; Людмила Фирмаль
редактирование Дэвида Грегорио С А А С а с Правый Интеграл, как функция x и C, непрерывен по x[theor2n°296], и по мере увеличения C до бесконечности-в z p A s t I, он стремится быть функцией И он предполагает непрерывность и интегрируемость для x от a до OO. Если применить результат правой части (7) к интегралу n°296, то можно перейти к пределу C—OO под знаком интеграла. В таких случаях не только предел Интеграла слабой части (7), а именно、
Смотрите также:
Решение задач по математическому анализу
| Случай интегралов с конечными пределами | Сведение к обыкновенному двойному интегралу |
| Предельный переход под знаком интеграла | Дифференцирование интеграла по параметру |

