Оглавление:












Движение в кулоновом поле (сферические координаты)
- Движение в кулоновом поле (сферические координаты) Очень важный случай центросимметричного движения Мистер Филд движется в подвесном поле U = b г (А является положительной константой). Посмотрим на сон Аттракцион Чаракурон U = -a / g. Из общих соображений, спектр Отрицательные собственные значения энергии дискретны ню (бесконечное количество уровней) и положительный спектр Энергия — Continuous.
Форма уравнения функции излучения (32.8) имеет вид d2R 2 dR / (/ + 1) d.2 + R + ^ (e + ^) r = 0. (36.1) r r dr Когда относительное движение двух привлекает Частицы, то м Вес. Полезно для расчетов, связанных с кулоновскими полями Вместо обычных специальных единиц измерения Все количество мы называем подвесной единицей ми как единица измерения массы, длины и времени Выберите соответственно P2 h3 w, -, —- j.
В следующих и последующих параграфах новое единичное уравнение Людмила Фирмаль
Там Все остальные единицы выведены отсюда. Единица энергии У тебя есть та2 / 1р? (36.1) присутствует везде <? R, 2 dR 1 (1 + 1 \ r + 2 (e + ^) R = 0. (36.2) dr2 r dr rz Дискретный спектр. Вместо параметра E Переменная r новое значение: n = 7 Вт ‘”=% ■ <36-3> Для отрицательной энергии n — положительное действительное число Номер.
Уравнение после замены нового (36.2) Ранг (36,3) будет в следующем формате + — R «+ -R ‘+ 1 П / (/ + 1) ~ 4 ~ р 7 ~ R = o (36,4) (Простое число означает производную по p). Если p мало, решение удовлетворяет необходимому условию Движение конечности пропорционально p1 (см. (3.2.15)).
- Найти Опустить вариации асимптотического поведения R для больших p (36.4) Получите уравнение в терминах 1 / ri1 / p2 R «= D / 4, откуда R = e ± p / 2. Заинтересованы в исчезновении навсегда Так что это решение работает как e_p / 2 для больших p. Принимая это во внимание, естественно сделать замену R = пл ~ р / 2удж (р) 1 (36,5) Тогда уравнение (36.4) принимает вид: Стадо «+ (21 + 2-р) w * + (n-1-1) o; = 0. (36,6)
Решение этого уравнения должно бесконечно расходиться Не должно быть быстрее конечного порядка p и должно быть конечным, если p = 0. Есть решение, которое соответствует последнему условию Вырожденная гипергеометрическая функция ω = F (−n + 1 + 1,21 + 2, p) (36,7) (См. Математическое дополнение §d) 1).
получим только из целого числа Отрицательное Людмила Фирмаль
Удовлетворительное решение Если оно бесконечно и удовлетворяет условию, (или равное нулю) значение (–n + 1 + 1), если Функция (36.7) является полиномиальным порядком (n-1-1). против Будучи чистым, он расходится бесконечно, как ep (см. (D.14)).
Следовательно, число n Положительное целое число и дано мне n ^ 1 + 1 (36,8) Вспоминая определение параметра n (36.3) E = — ±, n = 1,2, … (36,9) Это решает проблему определения уровня энергии дис. Математический спектр кулоновского поля. Вы можете видеть, что есть дьявол Конечный набор уровней между нормальными уровнями E \ = = -1/2 и ноль.
Интервал между двумя последовательностями Значительные уровни уменьшаются с увеличением n. Уровень Толще как значение E = 0 Дискретный спектр оперативной памяти замкнут непрерывно. нормально Для единиц формула (36.9) имеет следующий формат 2): Ј = -s? — <zb1 °> Целое число n называется главным квантовым числом. ошибка Квантовый номер циферблата, определенный в §32, равен пг-п-I-1.
Для определенного значения главного квантового числа число I Может принять значение I = 0, 1, …, n-1 (36,11) Всего N разных значений. К выражению энергии (36,9) Поскольку встречается только число n, все состояния с одинаковым I, но разными n, имеют одинаковую энергию.
Следовательно, каждое собственное значение является вырожденным Не только для магнитного квантового числа m ( Не только в поле симметрично в центре), но и с точки зрения чисел. Это окончательная денатурация (случайная или (Кулон) является уникальным для кулоновского поля. каждому Это значение I соответствует 21 + 1 различным значениям w.
Следовательно, вырождение n-го энергетического уровня Волновая функция устойчивого состояния определяется Формула (36,5), (36,7). Вырожденная гипергеометрия Если функция с целочисленными значениями для обоих параметров совпадает, Так называемый обобщенный, Многочлен Лагеры (см. Дополнительный математический §d).
по Это Радиационная функция должна быть нормализована условиями n — 1 (36.12) 1 = 0 Rnl = const -ple p / 2L% ll (p). OO о Окончательный вид выглядит следующим образом 1): 2 I {n I! ) • -r / n {Y j 2 / + 1 f \ _ n2 y [(n + /)! ] 3 V n) n ^ V n) 2 я (н + /)! н / + 2 (2 / + 1)! у (п — / — 1)! (P + g) ´ (2r) le ~ r / nF (-n + l + l, 21 + 2, -) (36,13) (См. §F, интеграл (f.6) x для вычисления нормализованного интеграла).
Рядом с источником формат Rni Нормальное состояние волновой функции я? Ио ослабляет экспо не в порядке r ~ 1, т.е. в нормальных единицах Среднее значение для различных степеней g рассчитывается по формуле: формула Общая формула для gc может быть получена с помощью Мул (ф.7). Где gk (s дает первые несколько значений s ложно и отрицательно j): Непрерывный спектр.
Сфера активного владения Значения энергии непрерывны, с нуля Бесконечность. Каждое из этих собственных значений является вырожденным Дано в бесконечной кратности, каждому значению E соответствует Существует бесконечный набор состояний, которые проходят через Все целочисленные значения от 0 до os (и все возможные значения) Значение данных /, м).
Число n определяется выражением (36.3) и переменной p te Крылья чисто воображаемые (36.14) На большие расстояния нит, г ~ Н2 / та. о о r = ^ [Зп2-1 (1 + 1)], r2 = ~ — [5u2 + 1-31 (1 + 1)], (36.16) n = — (36,17) Где k = 1 / 2E 1). Непрерывная радиальная собственная функция Формат спектра Ркл = + 1 +! «21 + 2) 2икр)» (36Л8)
Где Cki — коэффициент нормализации. Они могут представить Рена в виде комплексного интеграла (см. §D) Rkl = Cki (2kr) le ~ ikr. JL y * e «(l- ^ 2i» 4, (36.19) Взятый по контуру, показанному на рисунке 102). ниже При установке Ј = 2икр (t + 1/2) этот интеграл равен Симметричный внешний вид Rkl = Sy f e2ikrt (^ + ^) до 11 ~ l_1dt (36,20) (Путь интеграции поворачивает в положительном направлении Точка t = ± 1/2).
Из этого выражения Вы можете видеть, что ямс работает Это реально. Асимптотическое разложение (д.14) вас Гипергеометрическая функция Вы можете получить это напрямую Такое же расширение, как волновая функция R ^. Два члена (d.14) функции R ^ i являются двумя комплексными числами Но это сопряжено, и результат EGTG / 2K Rkl = SUP ——- X килограмм xRe exp expH (fcr- (7r / 2) a + l) + (l / fc) ln2fcr)] ^ + 1 + 1) i _ ^ _ W L IГ (/ + 1 ^ / к) ккI (36.21)
Нормализация волновой функции «по шкале к / 2тг» (т.е. Условие (33.4)), коэффициент нормализации Sy CM = 2keK, 2k \ V (l + l-i / k) \. (36.22) На самом деле, асимптотический R ^ я для больших г (Первый раздел расширения (36.21)) По общему виду нормированных волн (33.20) Центрально-симметричная непрерывная спектральная функция Поле.
Выражение (36.23) отличается от наличия бревен (33.20) Рифма аргументации знака; г растет медленно с увеличением г по сравнению с самим г, При расчете нормированной интегральной дивергенции На бесконечности существование этого термина не важно. Регулярное выражение G функциональный модуль (36.22) Мировой фактор Контейнерная функция.
Используйте известные свойства Функция G Rkl ~~ sin (кг + -2кг — I + 5 / Y г \ к 2 / (36.23) Г (z + 1) = zT (z), Г (г) Г (1-z) = 7tz S У нас есть далее Вот так C u = [g r t S * 2 + b (36-24) 8 11/2 (Если I = 0, продукт заменяется на 1). Достигнув предела, радиальный Особый случай функции с нулевой энергией. Ох, когда F (^ + 1 + 1,21 + 2,2кр) — + F ^, 2 л + 2,2кр) = = i _ 2g + (2g) 2 (2 / + 1) 1! (2Z + 2) (2 / + 3) 2! = (21 + л)! (2r) _ / _ 1 / 2J2 / + 1 (v / 8r), Где J2 / + 1 — функция Бесселя.
С коэффициентом Cm (36,24) Уменьшается до 0 См. «L / 87gЈy + 1/2». Найти здесь л / ж = J-Ju + xW & r). (36.25) / с- ^ 0 ВГ Асимптотическая форма этой функции для больших r 1) Ruki v / SM = (?) (36,26) коэффициенты с / о исчезают при переходе к нормализации «по шкале» Из энергии », то есть из функции R ^ i в функцию Rei согласно (33.5). Это функция Rei, которая остается конечной с пределом E-> 0. Поле кулоновского отскока (U = a / g) Ко непрерывный спектр положительных собственных значений Энергетика.
Уравнение Шредингера в этой области Получается из уравнения поля тяжести изменения Знак г. Следовательно, стационарная волновая функция Взят прямо из (36.18) тем же Обмен. Коэффициент нормализации снова Асимптотическая формула и результат Rkl = jЈf ^ (2kr) лейкрФ ({+ l + h2l + 2, -2 икр), Cu = + 1 + 1) I-P • 5-1 (36.27)
Асимптотическая формула этой функции для больших r Имеет форму Ркл к-син (кг — 2кг- + 5 / у , ‘2 (36,28) 6t = argΓyl + 1 + -J. Природа кулоновского вырождения. В классическом вождении Удельная частица кулоновского поля Метод консервации в этой области. Для поля притяжения A = — [pi] = const (36,29) г (См. I, §15).
В квантовой механике эта величина Rareta A = Ј-; ([p1] — [1p]), (36.30) Грамм 2 Гамильтониан — простой в проверке обмен I = р 2 / 2-1 / г Прямой расчет приводит к следующим правилам общения: Оператор A Station {Взаимный и Моментный Оператор: {k, Ak} = ieikiAh {AiiAk} -— 2iHeikih- (36.31)
Взаимная некоммутативность операторов A i Величины Ax, Au, Az не могут принадлежать квантовой механике Значение определяется одновременно. Каждая из этих опер Тори, например A z, коммутативна с теми же ингредиентами относится к lz, но не взаимозаменяемо с оператором момента квадрата T2.
Наличие нового хранилища, которое не измеряется Свинец с другими количествами хранения (§10) Для дальнейшего вырождения уровня это «Случайное» вырождение дис Критический уровень энергии. Происхождение этого вырождения может быть сформулировано С точки зрения улучшения симметрии (для сравнения Симметрия о пространственном вращении ноль), кулоновская проблема имеет в квантовой механике (В.А. Фок, 1935).
По этой причине для дискретных состояний спектра Если отрицательная энергия зафиксирована, Правая сторона последних отношений E (36.31) и введение 100 Ai, оператор u = Ai / г / -2E. Правила переключения для них Принять форму {k, Uk] = ieikiui, {щ, Uk} = (36.32) Наряду с правилом {U ^ lk} -ieikih, эти отношения формальны
Но это соответствует правилам переключения операторов на неопределенный срок Небольшое вращение в 4D евклидовом пространстве 1). Это симметрия кулоновской проблемы в квантовой механике 2). Вы можете получить снова из отношения переключения (36.32) Формула 3) для уровня энергии кулоновского поля.
Переписать Вместо них введите 1 и оператор ji = I a + d), j 2 = i (l-u). (36.33) Для них {ju, jik} = izikljih {j2i, j2k} = ieiklj2h {jii, j2k} = 0. (36.34) Эти правила формально соответствуют правилам переключения. Два независимых вектора трехмерного момента импульса. по Это собственное значение каждого из квадратов j 2 ji (ji + 1) и j2 (j2 + 1), где ji, j2 = 0, 1/2 D, 3/2, … 4).
С другой стороны С другой стороны, по определению операторов u и 1 = [gr] Простой расчет: lu = ul = 0, + И 2 = —1— 2 Е (При расчете суммы ++ 2 H снова заменяется на E). Отсюда Ji = J2 = -J (i + = j {j + 1) (Где j = ji = j’2), E = — ^ (2j + I) 2. маркировка 2j + 1 = n, yy = 1,2,3, …, (36,35) Требуемый результат E = —- Ts- достигнут.
Кратность 2 р Рождение уровней должно быть равным: (2ji + 1) (2J 2 + 1) = = (2j + l) 2 = n 2. Наконец, потому что 1 = ji + j2, ji = j * 2 = (n-l) / 2 орбитальный момент l проходит через значение От 0 до 2j = n-1 x). Задача 1. Определить распределение вероятностей различных значений Импульс основного состояния атома водорода. Solution2). Волновые функции основного состояния φ = DuUoo = ~ ^ e g • V * —
Волновая функция того же состояния в p представлении может быть получена из Да, как неотъемлемая a (p) -Jφ (m) e ~ r1r dV (См. (15.10).) Интеграл рассчитывается путем перемещения к сферическим координатам Нац с полярной осью вдоль р, в результате «(P) = (I T 7 P Плотность вероятности p-пространства равна | a (p) | 2 / (27r) 3. 2.
Определить средний потенциал поля, созданного ядром и электричеством Основное состояние г атома водорода. Решения. Средний потенциал («электрон Лак в любой точке r легче всего определить как шар Симметрично-симметричное решение уравнения Пуассона с плотностью заряда р = -у 2: ^ 1-2 г г др = 4е »
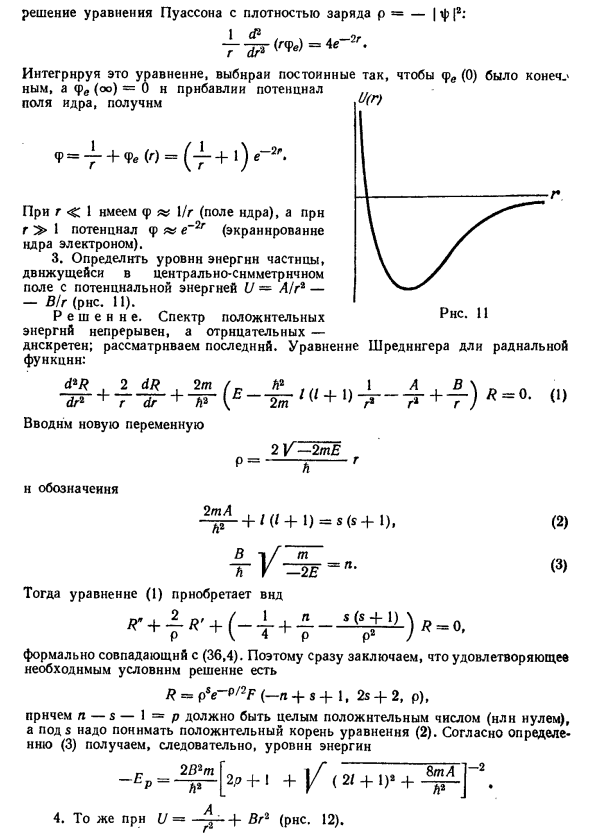
Интегрируйте это уравнение, выберите постоянную и <pe (0) Infinite, a <pe (oo) = 0 и добавление потенциала ядерного поля, (F = 1 / g + (fe (r) = (1 / g + 1) e-2 g. Для r 1 «1 / г (ядерное поле) и r 1 Потенциал у вас? ~ E_2g (ядерное экранирование электронами). 3. Определить уровень энергии движущихся частиц В центрально-симметричном поле с потенциалом Энергия U = A / г2-В / г (рис. 11).
Решения. Спектр положительной энергии Прерванный, отрицательно-дискретный, на рассмотрении Ешь последний. Радиальное уравнение Шредингера Особенности: д р ^ 2 дР ^ 2 т dr2 g dr H2 Введите новую переменную E- P = Т2 +! ) 4 г 2 \ J-T E ——- г N А б R = 0. И спецификация: 2t A + 1 {1 + 1) -с (с + 1), -2 Е Уравнение (1) принимает вид: R (1) (2) (3) + 2 L ‘+ (L + P.-Ј (Ј + 1) P V 4 p p Формально совпадает (36,4).
Поэтому мы скоро завершим Решение для создания необходимых условий R = p∈F (−n + s + 1, 2s + 2, p), Где n-s-1 = p должно быть положительным целым числом (или лем) и s нужно понять положительный корень уравнения (2). По словам Определение (3), таким образом, получить уровень энергии 2 -E v = 2 В т P2 2p + 1 + * / (21 + I) 2 + 8 тА P2 4.
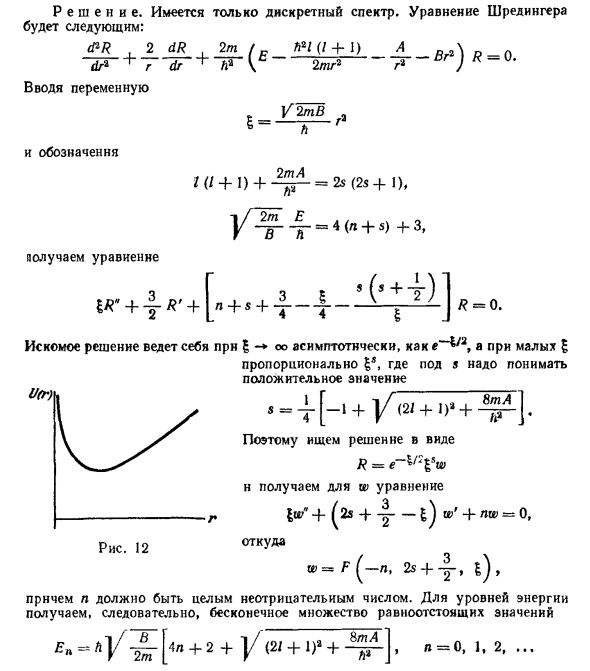
То же самое для U = 4m + Br2 г (Рисунок 12). け け Только я стою, все еще дискретный Шредингер выглядит так: d2R 2dR 2t / P21 {1 + 1) _ A. _ д-р д-р P2 V 2 тг Спектр. уравнение Br2 D = 0. 166 Движение в центрально-симметричном поле V Введение в переменные И обозначения: Получить уравнение л / 2тв 2 Ј = —z — g 1 (1 + 1) + = 2 с (2 с + 1), Я 2т Э.
Хо ‘— 4 (n + s) + 3 В п ЈR «+ -D ‘+ 2 3 с (с + 1/2) n + sH ——- ———- ^ 4 4 я R = 0. Rp irp obes te devine esher eomoxIo является асимптотическим, e ^ / 2, и Должно быть положительно пропорционально каждому чтение 1 s = — 4 -1 + ,, (2, +!)> + *! Ј Итак, ищем решение формы R = e «? / 2Ј2w И, Јw «+ (2s + 3/2-Ј) r» / + nw = 0, Откуда w = F (−n, 2s + 3/2, Ј), Где n должно быть неотрицательным целым числом. Об уровне энергии Таким образом, вы получаете бесконечный набор одинаково разнесенных мнение En = ON 4n + 2 + 1 / (2Z + 1) 2 + ^ n = 0,1,2, …
Смотрите также:
| Разложение плоской волны | Движение в кулоновом поле (параболические координаты) |
| Падение частицы на центр | Возмущения, не зависящие от времени |

