Разложение плоской волны

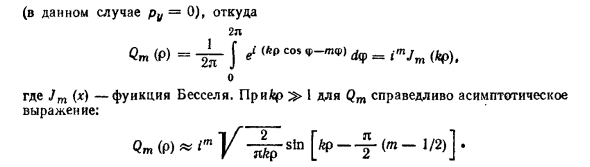
Разложение плоской волны

• Разложение плоской волны. Рассмотрим свободные частицы, которые движутся четко положительный импульс по оси z p = кН. Волновая функция таких частиц φ = const -elkz Расширить эту функцию в терминах волновых функций Движение в определенный момент.

В гонке При рассмотрении энергия имеет четкое значение E = k2fi? / 2м, понятно, что будет входить только желаемое расширение Та же функция к. Кроме того, функция Elkz является Осесимметричная вокруг оси 2: только функции, не зависящие от угла (то есть функции Когда m = 0.

Эти константы удобно определены Сравните и вылейте коэффициент Людмила Фирмаль

Таким образом, он должен выглядеть следующим образом. Oh Oh Oh & Ikz _ y schft = y ^ aiRkiYio, 1 = 0 1 = 0 Где / это константа. Заменяющие выражения (28,8) и (33,9) Функция Y / O и я? & / оо, e- = Јc, p, (c o S «^) ( 1 = 0 Где C / — еще одна константа. (g cos b) n в обеих разработках Часть равенства власти.

На правой стороне равенства Этот термин существует только в пятом члене. I> N расширение Функция излучения начинается с увеличением порядка r. Когда η> I, порядок многочлена Pi (cos) низкий потому что Член cos1 в Р / (cos #) имеет коэффициент (21) \ / 21 (1 \) 2. (См. Уравнение (стр. 1)). Используя уравнение (33.13), Период расширения на правой стороне равенства, который представляет для нас интерес (2l)! (Fcr cos in) 1 ‘} 1 2 г (Z!) 2 1 • 3. , , (2 / + 1) *

• Левая часть соответствующего уравнения (расширенная Термин exp (ikr cos ×)) (■ IKR COS в) 1 P ’ Если обе величины равны, вы найдете C / = (–r) 1 (21 + 1). так Итак, наконец, получить желаемое разложение оо, = Ј (- <>> (2! +1) P, (ω8α) (Γ) (iЈ) it (34.1) 1 = 0 На больших расстояниях оно становится асимптотическим форма о elhz «^^ i l (21 + l) P / (cos6>) sin (^ kr- (34.2) r / = o В (34.1) ось z выбирается в направлении волнового вектора Плоская волна k.

Это разложение дальше § 34 Разложение плоской волны 149 Общий вид, который не предполагает конкретного выбора координат Ось ось. Для этого воспользуемся следующей теоремой Функция мяча (см. Стр. 11), выраженная с его помощью Линейность P / (cos $) по сферической функции от направлений k и r (Угол между): о ^ = 4 ^ Ј6 K b) Y ^ (|) Y r m («). (34.3) / = 0 м-1

Из продукта кг симметрия формы Людмила Фирмаль

Функция ji (kr) (определена согласно (33.11)) , таким образом, ясно видна Векторы k и r (две сферы Функция является признаком сложного сопряжения — это не имеет значения).

Нормализовать волновую функцию elkz равным единичному плоту Стохастический поток, то есть, чтобы соответствовать Поток частиц через единицу площади (параллельно оси Z) Сечение, через которое проходит одна частица за единицу времени. Есть такая функция gr = — ± -eikz = x [^ e ikz (34,4) (V — скорость частицы, см. (19.7)).

Равное умножение с обеих сторон у ^ т / кН условие (34.1) и нормализовано Функция Φ ± m = Д ^ (г) В / м ((9, ^), OO φ = ^ yfn (2l + 1) — (Фоо〜 ^ ш) — / = 0 Квадратный коэффициент этого (или ^ w) коэффициента Разложение определяет вероятность в соответствии с общими правилами Частицы входят (или расходятся) в центр Посередине) есть момент у меня в потоке (к началу) Координаты).

Волновая функция elkzjy / v Если поток частиц равен единице плотности, эта «вероятность «ност» имеет размерность длины в квадрате. Она может Это четко интерпретируется как значение «целевой области» ( Xy самолет, где падает падающая часть ца, если этот момент я.

Указывает это значение через с / at = J (2 / + 1). (34,5) Если значение I велико, общая площадь воздействия Интервал AI (например, 1 A 1 ^ 1) для значения I равен Y «m / u 4 -2 / A / = 27T ^ A /. ^ k2 p2 искусственный интеллект Замена мгновенного W = pp классической формулой (P — это так называемое расстояние удара) Введите 27gAr, Это соответствует классическому выражению.

Эта ситуация Это не совпадение: позже вы увидите это с большой ценностью В разделе I движение является квазиклассическим (§49). Оспаривать Расширяет плоскую волну в соответствии с волновой функцией определенного состояния Значение проекции момента на ось y и проекция импульса r На одной оси.

Решения. Цилиндрическая система координат y, p, (p с осью вдоль оси Y. Волновые функции для этих состояний имеют вид Qm (p) e’irnipegPyU ^ n. Угол (считая р от оси Z, разложение Написать как о икз икп о с о? \ l gl / \ imip э-э-у ^ CJm \ P) Ј м = -оо (В этом случае ru = 0), почему 2р Qm (p) = — / exp [z (fcpcos (p-m (p)) d (p = zmJm (Јp), 2i7t J 0 Где Jm (x) — функция Бесселя. Асимптотическое поведение Qm для kp 1 Формула: Qm (p) ~ i ™ \ I-7-sin

Смотрите также:

• Решение задач по физике

Движение в центрально-симметричном поле	Падение частицы на центр
Сферические волны в физике	Движение в кулоновом поле (сферические координаты)