Оглавление:



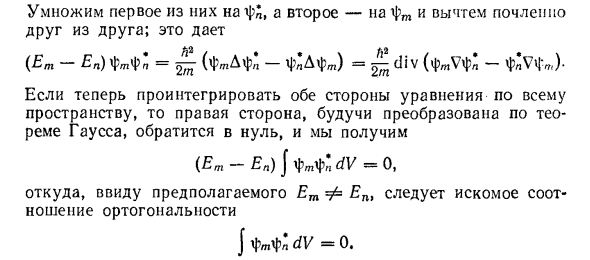

Плотность потока в физике
- Плотность потока. В классической механике скорость частицы v равна Коэффициент импульса p = mv. В квантовой механике И следовало ожидать, что между соответствующими Связанный оператор.
Это можно легко проверить, рассчитав Оператор с общими правилами дифференцирования v = r Тора во времени (9.2): V = — (Я ГГ). час Используя уравнение (17.5) и уравнение (16.5) для H, Мы получаем v = п / га (19,1) Такое же отношение, очевидно, происходит Скорость и импульс, а также собственные значения между этими средами Значение в любом состоянии.
Поэтому факт не важен Скорость вместе с координатами Частица находится в точке в пространстве Людмила Фирмаль
Скорость как импульс частицы не может быть определена Значение в то же время, что и координаты. Но скорость Умножим бесконечно малый элемент времени dt Увеличьте смещение частиц за время dt. Впервые у него больше не будет определенного пола.
Уже в ближайшее, почти бесконечное время. Обратите внимание на полезные формулы для операторов / производных Определенное количество f (r) времени, это Частица Deus. Обратите внимание, что / коммутативно с C / (r) узнать ; = 1 (i / — / i) = ^ / — / p2), Использование (16.4) p2 / = p (/ p- ^ v /), / p 2 = (p / + iH Vf) p Найдите выражение, которое вы хотите / = ^ (P V / + V / -p). (19,2) Далее найдите оператора ускорения. У нас есть v = {(Хорошо-уу) = ^ (я p-pH) = -Тебе.
- Используя уравнение (16.4), nri = -VC /. (19,3) Это операторное уравнение вида точно соответствует Классическое уравнение движения (уравнение Ньютона) Haniki. Интеграл / | Ф | 2сЛ /, занял конечный объем mu V — вероятность нахождения частицы Это том. Вычисляет производную по времени от этой величины Измени меня и мы j t J | Ф | 2dV = J (ф ^ + ф * ^) dV = ^ J (ФЯ * Ф * -Ф * ЯФ) dV.
Заменить здесь H = n * = — ^ A + U (x, y, z) 2 тонны И использование личности FDF * _ f * DF = CPU (FUV * -F * UV), Мы получаем j | Φ | 2dV = -J divj dV, j m 2d, V = -jijd f. (19.5) дт Где j представляет вектор 1) j = — (ФёгаёФ * -Ф * градФ) = — (Фр * Ф * + Ф * рФ). (19,4) 2т 2т Интеграл divj можно преобразовать согласно теореме Гаусс интегрировать по замкнутой поверхности Том V: d дт
Интеграл этого вектора на поверхности Частицы пересекают эту линию в единицу времени Топ Людмила Фирмаль
Это показывает, что вектор j называется вектором плота Стохастическая плотность потока, или просто плотность потока. . Вектор j и плотность вероятности | Ф | 2 уравнение ^ + divj = 0, (19,6) Ветхий Завет Аналогично классическому уравнению неразрывности.
Волновая функция свободного движения представляет собой плоскую волну (17.9) — можно нормализовать, как описано Поток частиц одинаковой плотности ( Передайте единицу площади поперечного сечения Среднее одной частицы в единицу времени). Такие функции Φ = -T = exp [- ^ (. Et-pr) l, (19.7) год / год 1 P J Где v — скорость частицы.
На самом деле, заменить (19.4) j = p / mv, то есть получить единичный вектор направления движения. Удобно, как это показано прямо из уравнения Уравнение Шредингера предполагает волновую ортогональность Функция состояний с разными энергиями. ft и φn — 2 Такие функции, они соответствуют уравнению H2 «^ Ft ft = etft ^ 2 тонны — ^ — Af * +, если * n = Ep *.
Умножьте первый элемент на a, а второй элемент на ft Один за другим Это дает (Et-En) ftp1 = ^ {[phi] tAf * n-> * nAft) = f-diy (ftt ** — p * ^ ft). зм зм Если мы интегрируем обе части уравнения здесь Пространство, преобразованное по теореме, то справа Гаусс исчезает и мы получим (Et-En) J ftPn dV = 0, Необходимые меры принимаются с учетом предполагаемого Et f En. Носить ортогональность J ftf * n 4U = 0.
Смотрите также:
| Уравнение Шредингера | Вариационный принцип в физике |
| Основные свойства уравнения Шредингера | Общие свойства одномерного движения |

